Yesterday, I had a lot of reasons to think about the question of mechanical advantage involving ladders. The 40-foot extension ladder that I ordered (one has to special-order such things) finally arrived and it was time to clean out the gutter on the upper edge of my house.
In case you’ve never done it, the power curve on erecting a ladder appears to me to be non-linear. But I don’t actually know for sure; hence this posting.

Ladders terrify me, btw. There is something about being the plumb-bob on a pendulum ride that ends in impacting a surface – brr, no thanks. Actually falling seems to be less scary but when a ladder starts slipping sideways, you’re defining an arc and (I guess?) you’ve got more distance for your fall to accelerate over.
The ladder in the picture is not at an angle, it just looks like it from where I was standing and how I held my camera. If it were at an angle, it would be falling.
So, I kept trying to figure out the 8th-grade physics of the mechanics of this thing.
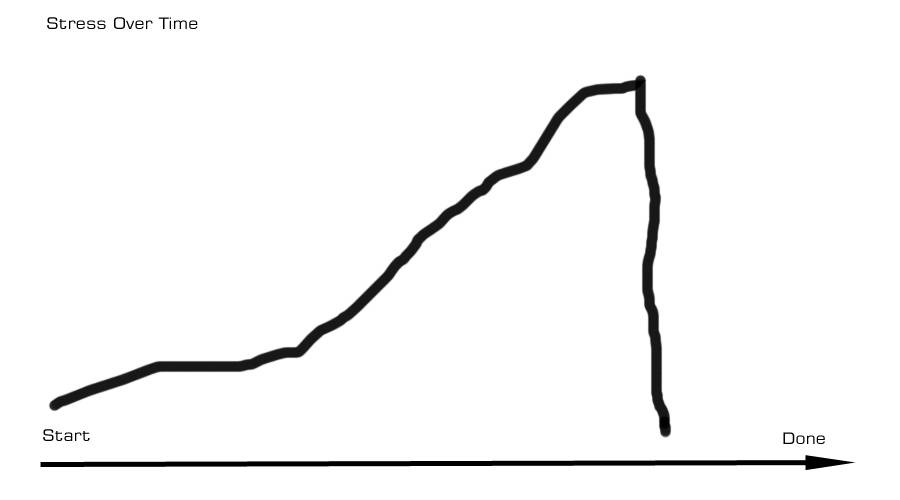
It starts out “not very heavy” then gets progressively heavier and heavier, then you have one big push where it seems you’re dead-lifting the whole damn thing, and – finally – it weighs nothing because it’s standing on its end. When it’s completely upright you can hold it upright with finger-strength because the ladder is its own fulcrum, I guess, where it contacts the ground.
I am not going to get into the part where you raise the extension by hauling on the little pulley while keeping the whole mess upright – if it starts to go, you just have to get out of its way. And leaning it against the wall isn’t great, either – you have to kind of plant your feet as a brace and let the thing tip away from you while you hold onto the pulley-rope. If you do it right, the ladder extends as it falls, and the fall is slowed by your puny weight and it does not smash a hole in your siding.
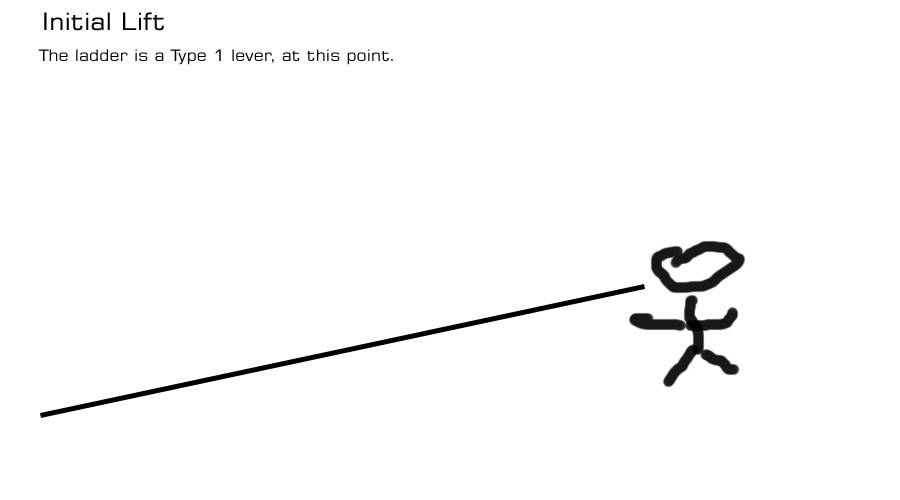
Here’s what I think is going on, that creates that weird load curve. We start out with a type-1 lever. The length of the lever gives the ratio of its mechanical advantage. The ladder weighs about 150lb, but when you just lift one end it feels like it weighs maybe 40lb. You can stand there all day, thinking, “ready, steady, go!”
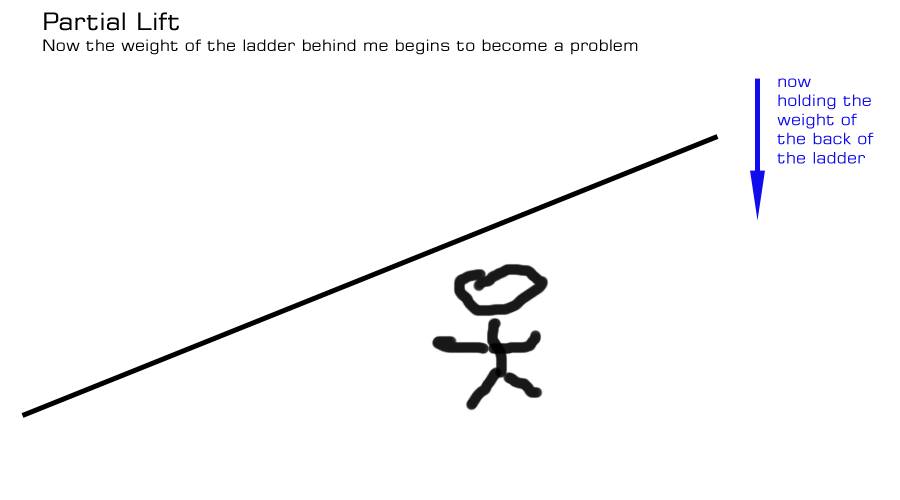
Then, you walk forward (being tall helps, I am pretty sure) and as you move toward the fulcrum, you no longer have any mechanical advantage over the tail end of the ladder. In fact, the closer you get to the middle of the ladder, the heavier it appears to be (I think). I guess what we are experiencing is that we are becoming the fulcrum, or something like that. Basically, we are now a “teeter-totter” and it feels like the entire weight of the ladder is on us. This is “the moment of suck” – the grunt stage. I’m not sure what’s going on, in terms of mechanics, but it feels like I’m doing an overhead press of the entire weight of the ladder – but I know I’m not because I’m not strong enough to do that. So there’s still some mechanical advantage but I think it’s working against me. I’m not sure. Is the butt-end of the ladder now a type-1 lever against me?

After the grunt stage, you have the ladder vertical and you can hold it indefinitely, effortlessly, while you enjoy your heart attack. Don’t do this on a windy day, because if the wind begins to deflect the top of the ladder, it’s now got leverage against you and (if I am thinking correctly) a small wind-push will equate to a large wind-push down at the fulcrum. You’re at the fulcrum, and the fulcrum is what gets squished when leverage is being applied.
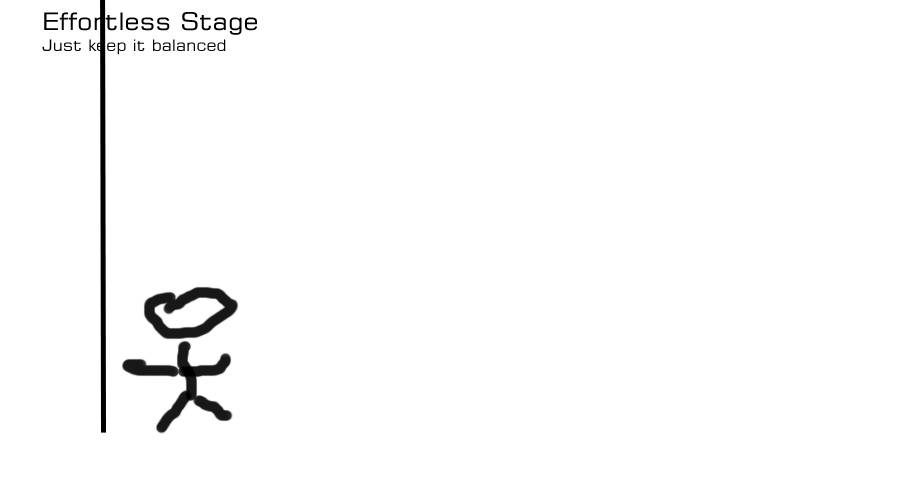 There you have it: ladderology.
There you have it: ladderology.
I guess the question I have is, am I right that the stresses on the lifter change on some sort of curved function, or not? I get type-1 and type-2 levers, but I don’t understand what the fulcrum experiences. Wouldn’t that be stress equal to the amount of mechanical advantage? I.e.: if my mechanical advantage makes something feel 1 ton lighter, doesn’t that imply that the fulcrum is getting 1 ton of stress on it? I’m not even sure if representing the experience on a curve is the right way to do it, but it’s weird, is all, that the thing starts out manageably light then becomes ball-bustingly heavy, then weighs nothing – all within a few seconds. And it has to be “a few seconds” because if you stall out and stop moving at the “Grunt” stage you’d better start thinking about how you’re going to walk back or land the ladder, because it’s not going up.
That was my yesterday. After that, I was done, and took a cool shower, made some szechuan chili oil, had some angel hair pasta with peanut/fire oil sauce, and played Subnautica.

I have a friend that is a physics professor. I will send this on to him.
Torque and Trig.
>Actually falling seems to be less scary but when a ladder starts slipping sideways, you’re defining an arc and (I guess?) you’ve got more distance for your fall to accelerate over.
.
That’s not right.
.
Slipping sideways is bad. But not as bad as a direct fall from the same height. For one thing, you have more time to plan your landing. Part of your landing plan should consider where the ladder lands.
.
I took and passed calculus 50+ years ago so I won’t pretend to give exact numbers. As the sideways fall starts most of your weight is on the ladder. It’s actually supporting you. Its support diminishes to zero just before impact. But your impact energy is less than a direct fall.
.
If you take a hose with you tie a rope to the hose and carry the rope tucked into your belt such that if something unexpected pulls on the rope it will drop free. Much better you climb twice than need medical assistance.
.
It’s best to have an assistant. Especially when raising or lowering a ladder of that size.
Peter B@#3:
If you take a hose with you tie a rope to the hose and carry the rope tucked into your belt such that if something unexpected pulls on the rope it will drop free. Much better you climb twice than need medical assistance.
There was a sketch that they used to do on Benny Hil, involving a bricklayer who was on a ladder with a bunch of bricks on a pulley, and he fell and hit them several times. I don’t remember it because: ladders.
My guess is that you are involved in a class 3 lever. The fulcrum is, should be, fixed at the base of the ladder and the load is the weight of the ladder itself. As you advance under the ladder more of the load is beyond the point where force is being applied, i.e. your position under the ladder.
When you are at the end of the ladder, the entire load is spilt between the foot of the ladder and your lifting. So you would be lifting about 50% of the weight. As you move under the ladder you have to lift a greater percentage of the weight of the ladder. And this change in force will be linear. But there is another factor involved in most ladder raising. Keeping the bottom of the ladder on the ground.
If the ladder is not fixed to the ground, when you reach the half-way point along the ladder you will be carrying the entire weight of the ladder. The end of the ladder will raise up because the fulcrum has now shifted from the other end of the ladder to the center. To prevent that from happening, you have to apply additional force to keep the end of the ladder down. I typically do this by grabbing some rungs a few feet apart and creating another moment arm. My upper hand is pushing up the ladder while my lower hand is holding the ladders base to the ground. At this point I am exerting more force than the weight of the ladder, and unless you are fairly close to the end (no more than ~5 feet) it can be very hard to raise a ladder this way. With a 40′ extension ladder, the unextended length is 20′, so the center of the unextended ladder is 10′, and you can get to about 5′ from the end while raising it. That’s about as long a ladder I feel I could raise by myself, and even that would be difficult. I’d put weights on the bottom (or dig a couple small holes in the sod) to hold it in place.
Putting weights on the end of the ladder to hold it down (usually another person to stand on ends) makes it a lot easer to put up as doing so reduces (or eliminates) any additional force to hold the end of the ladder against the ground while raising it. Without doing any analysis, I suspect that even with a fixed fulcrum you would be carrying the entire weight of the ladder at 45 degrees, but as you continue to raise the ladder some of the force necessary to move it will come from the fulcrum. and the force will drop off. Without a fixed fulcrum at the end of the ladder you are going to be lifting as much as twice the weight of the ladder, the entire weight to lift it, and most of the entire weight again to prevent the ladder from sliding until the ladder gets vertical enough that the forces of friction on the base of the ladder are enough to hold it in place.
But these are just my initial thoughts. I could be wrong.
Looking at your diagram the biggest error is that you only have one arrow pointing down, for the weight at the free end of the ladder.
For a simple unloaded ladder it’s much more useful to think of its weight as being applied at the centre of mass. The end of the ladder that’s resting on the ground is your fulcrum, and your shoulders are providing the counter force to keep the ladder up. So when you start lifting your distance to the fulcrum is twice as large as the weight’s distance to the fulcrum, meaning you carry half the weight. At the midpoint you’ll be carrying the full weight, which you’ve noticed because the ladder has become a teeter totter. But as you keep going you’ll have to carry multiples of the weight proportional to how close you are to the fulcrum. This is your grunt stage and mechanical advantage is indeed working against you.
If you were an infinitesimally small spherical cow you could keep that up until you’ve reached the very base of the ladder and finally get it fully upright with an application of infinite strength. But you’re not an infinitesimally small spherical cow and if you look up you’ll see that not only has the end of the ladder moved upwards while you were pushing, it has also moved closer to the fulcrum horizontally. As you complete its quarter circle motion, the end will also start horizontally moving closer to YOU. Eventually the centre of gravity of the ladder is above you, and you’re merely carrying the weight of the ladder itself again. Then the centre of gravity passes you and we’re back into class 2 lever territory. This is the point where you’d take the ladder off your shoulder and push those final few degrees until it’s fully upright with your hands alone.
re: The bricklayer’s letter. Several versions, one played yearly on a ‘classic comedy’ program on the CBC. Can’t find it, but this is probably the text.
Arrrgh, no link. Does this work
“http://www.physics.smu.edu/scalise/www/misc/bricks.html”
Ohh, here’s the one I remember hearing.
“https://www.youtube.com/watch?v=LOy2GuaP8Mo”
Peter B @3:
Actually, if you ignore friction, you’ll hit the ground slightly faster if you stay on the ladder than if you jump off from the top.
It’s the usual problem of converting potential energy to kinetic energy. Let’s assume no friction, and the ladder (length L) is initially vertical. We’ll also assume the mass of the ladder is the same as the person on top, and the person is a point mass (shades of spherical cows!).
The potential energy starts out as
mgL + mgL/2 = 3mgL/2
The first term is the person’s PE, the second is the ladder’s.
As it falls sideways, the kinetic energy for each part is given by Iω²/2 (see here), where I is moment of inertia and ω is the angular velocity. For the person, the moment of inertia is mL². For the ladder, it is mL²/3 (see here). So total KE is
2mL²ω²/3
Now, Lω is the angular velocity v of the person, so when it hits the ground, and all PE has been converted to KE, we equate the two expressions to get
3mgL/2 = 2mv²/3
So v² = 9gL/4
Whereas if you jump off the ladder, you’ll have
v² = 2gL
I think you would land at the same speed: potential energy (you at top of ladder) gets turned into kinetic energy (speed), irrespective of path. If the end of the path points down, bad news. If it ends up (as in a kid’s slide) horizontal, good news. Sliding ladder (with end of ladder fixed) , alas, ends up with you falling straight down.
On the effort to raise ladder, at some point the feet must become pivots. The maths (ah ah! A Brit!) is simpler if the feet are always treated as pivots: then where-ever you are on the ladder, you are pushing at right angles to it. Initially this is vertical at the end opposite the feet, then the force rotates until (with the ladder vertical) the force is horizontal, and applied at a Marcus Unit of Height above the feet. The place of maximum force will depend on the length of the ladder (in units of Marcus). Think of a 2M ladder vs a 20M ladder.
astringer @11:
You’re ignoring the potential energy (and kinetic energy) of the ladder. See #10.
These illustrations are quite expressive, and enough to dissuade me from ever lifting a ladder so thank you.
me @10:
Terminology slip-up. ω is the angular velocity, v is the velocity.
Someone should do the math. A spherical cow is connected to a stiff vertical 10-meter massless rod on level ground. This assembly is hit by a butterfly wing. It starts ever so slowly to fall under the influence of uniform gravity.
What are the vertical and horizontal forces exerted on the ground by the rod as the rod/cow assembly falls? You may assume a frictionless pivot between the rod and the ground.
At what speed does the cow hit the ground? Compare that speed to that of the cow falling 10 meters.
I could work this out in 1965. Not so much today.
Peter B @15: I did the math in #10. Just remove the terms involving the mass of the ladder, and that gives
mgL = mv²/2
which gives the same v as the cow falling a distance L.
A spherical cow! Back when I used to shear sheep I was looking for a completely flat sheep. No second cuts on a flat sheep! I never even dreamed of a spherical sheep. Most fortunately.
Start simple. The weight of each ladder segment is approximately spread equally over its length. The center of gravity of a ladder is approximately at the center, regardless of whether the ladder is a single segment or multiple segments.
With the ladder starting flat on the ground, lifting it from one end is a simple lever calculation. There are no dangerous complications unless/until you work your way to the center of gravity. If you go past that, then the ladder will attempt to rotate around the fulcrum, which is you.
You can buy screens that fit on top of the gutter and allow water to drain into the gutter while keeping leaves out. This should greatly reduce the frequency with which you need to deal with this.
You can’t comb a spherical sheep flat.
Rob Grigjanis,
The ground exerts a vertical force on the rod even as the cow/rod assembly is falling. Think of it this way: halfway down if the ground were replaced by tissue paper over a hole in the ground that lack of support would be obvious. It’s the ground pressing up that makes a difference.
Think of the cow extending a foot touching the ground. That foot pressing down would slow the cow’s fall. I’m guessing here: the effect of gravity has to be multiplied by sin(t) where t is the off-vertical angle.
Peter B @20: The bottom of the ladder is fixed. The force acting on the cow is (as you say) mgsinθ at 90 degrees to the rod, where θ is the rod’s angle with the vertical. So the equation of motion is (from Newton’s second law)
d²θ(t)/dt² = (g/L)sinθ
which is (no surprise!) the equation for an inverted pendulum. There is no simple solution for this, except for very small angles, but we want the speed at 90 degrees from vertical.
But we don’t need the solution. We just want the speed just before the ladder hits ground, and that can be obtained from conservation of energy; if the zero of PE is chosen at ground level, all the PE is converted to KE. That’s what I did in #10.
I’m not sure what you mean by “It’s the ground pressing up that makes a difference.” Yeah, the difference from free fall is that the rod with one fixed end constrains the cow to follow the path of a quarter circle. That’s been accounted for.
The bottom of the
ladderrod is fixedThanks Rob, posts crossed @ 10. You are right, I was (by accident) ignoring the mass of the ladder (but surely it is small ?). BUT, we now have the issue of what happens if Markus lets go of the top of the ladder (at about 30 degree I think) falling the rest of the way in a parabola: this gives some of the PE converted to horizontal KE, therefore less vertical KE, and hence a softer landing. Staying gripped on generates a whiplash in the final stages… decisions decisions!
I couldn’t resist properly mathing it out, and here’s my result: https://www.desmos.com/calculator/vb925dcwxi
It’s still a fairly rough approximation, because first of all I’ve assumed your pivot point is fixed, and then you’re a rectangle with height h and width a, pushing horizontally against a ladder of length l and weight w. The horizontal axis is the distance travelled from the free end of the ladder, and the vertical axis is the load you actually have to carry at each distance.
Playing around with the sliders is pretty fun, and you can easily see that being taller does make putting up ladders a lot easier, and so does stretching out your arms to push the ladder when it’s almost vertical (simulated by increasing the a value).
astringer @23:
Marcus said his ladder was 150lb, but I just didn’t want two different masses; extra typing. But I did show the separate contributions from ladder and person, so anyone who wants can use different masses in the equations.
Imagine the ladder split into two separate but bound components.
One the one side you have a zero-mass infinitely rigid lever, which you are trying to lift. That applies a certain torque to the fulcrum, but as you get closer and your mechanical advantage decreases the amount of applied torque decreases linearly.
One the other side is a fixed weight a fixed distance from the fulcrum. That exerts a torque in the opposite direction, which you must match to proceed, and as you proceed that half of the system rotates around the fulcrum. As such the response of its torque to your progress is not linear, but a trigonometric function of its angle, but its mechanical advantage does also decrease with your progress.
That function starts by decreasing very slowly, so it is outpaced by the linear decrease in your mechanical advantage, so it has relatively a greater advantage over you, so gets harder. But that rate increases over time until it also reaches linear – matching your own decrease, so it stops getting harder. The rate continues to increase thus its rate of loss of mechanical advantage exceeds your own and it gets easier. This continues until you reach the fulcrum and the weight is at vertical at which point it is exerting no torque and you don’t have to counter that any more (zero effort!), the only effort required now is to counteract its inertia.
How did you clean that gutter Before Ladder, and why did you change now?
Could you attach something to your drone to clean gutters with your feet &/or butt securely on the ground?
I am beginning to think a return to cave living sounds attractive.
Weirdly enough I can never remember cleaning out the eves troughs in the family home. Perhaps not enough close trees? There was lots of muck in the cistern though.
Regarding lifting the ladder, which has a mass m:
Suppose you can lift it all the way up from one end (stretchable Marcus!). At a given angle θ between ladder and ground, the torque being applied is proportional to Lcosθ, where L is the length of the ladder. The cosθ gives the ratio of the gravitational force perpendicular to the ladder.
At that same angle, if you want to support the ladder from a distance d from the fixed end, you still have to apply the same torque, so the force you need (weight you feel) is (L/d) times the force you need to support it from the far end. So relative to the force you need to barely pick up one end, which is mg/2, the force is mg(L/d) (cosθ)/2
Now, suppose the support always comes from a fixed height h. Then h = dsinθ, and the force you need is
mg(L/h) (sinθcosθ)/2 = mg(L/h)sin(2θ)/4
Of course, it’s been a while since first year statics!
Practical advice:
Longer ladders benefit more from having help. Having a helper with a 12′ step ladder is good, handy, and can speed things up. With a 40′ extension ladder it is pretty much a requirement.
Anyone can reliably approximate the ideal set-up angle by placing your toes at the bottom and reaching out horizontally with your arms. When you can grip both rails as your boot tips touch the bottom it is very close to ideal. Human bodies just happen to be proportioned for this to work out.
To raise an extension ladder place the bottom against the house, or other firm object, a helper footing it is great. Then walk the ladder up from the far end. Keeping your arms straight helps.
When using an extension ladder it pays to tie off the top. For shorter jobs, and those going only part way up a building a single screw can be installed as an anchor point. The anchor needn’t be large enough to hold the worker, just heavy enough to keep the ladder from sliding sideways or falling backward.
A ladder that goes to, or in the case of roof access (the top at least 3′ above the roof deck), your best anchor is usually to get a rope over the roof and tied off on the ground on the opposite side of the house. A lot of contractors tie off to vehicles. Carelessness in this situation, with the vehicle driving off, leads to visually fascinating accidents and epic stories … after everyone is out of the hospital.
Easiest way of getting a rope over the roof is to use a throw-line and bag. A light line (parachute cord works well) and weighted bag easily made from discount store gym socks, one inside the other (padding reduces injuries and damage) and a handful of steel nuts or about $1.50 in pennies. The throw-line is used to pull the heavier rope over.
Aside – $4 in pennies, a couple of pool balls, or bars of soap in doubled gym sock will drop em like a sack of taters if swung vigorously. Hardly even leaves a mark. No sir, I don’t know what happened. Looks like he took a nap. Narcolepsy?
If you will be moving the ladder along the roof edge it is usually easy enough to leave some slack and whip the slack in the direction of the move while you are at the top. Then climb down and shift the ladder. Slack makes the rope less effective in stopping slips but it should still stop any actual fall. If things go sideways the key is to hang on. Once the ladder stops sliding you can still monkey down. Panicking and jumping typically leads to worse injuries.
If the ladder is being used for roof access for longer projects firmly tying both top and bottom pays dividends in safety and speed. Most accidents happen transitioning from ladder to roof, or back. That last second when you haven’t established footing on the roof and are still dependent upon a light touch on the ladder is exactly when things go sideways. I’ve seen it. I’ve done it. Rattles me every single time. Three feet of ladder above the roof to hang on to and having everything tied off is the way to go.
At a very minimum, get help.
A good alternative is to hire the job out. Younger men heal faster.
If I just had to do it myself I might rent a crawler bucket. They are a bigger thing now on job sites. We used to hang lights on buildings with three guys and a 40′ extension ladder. We could hang just a precious few light in eight hours. Up and down we would climb. My Now they do three times the work with a just one or two guys and a lift.
They are mighty handy for gutter work, painting, tree trimming, roof repair, you name it. Far easier, faster, and safer than humping around ladders.
Coordinate with neighbors who might use a lift and split the cost. They usually go by the day and some companies don’t count weekends. You may get three days, and share costs with several people doing many jobs, for the cost of one.
Hiring out or renting a lift isn’t cheap but neither is a broken leg. And don’t get me started on back injuries.
Sorry if this is all old news. Everyone knows this stuff, and yet so many get hurt. I’ve spent a lot of time on ladders. I’ve never been seriously hurt but there have been many close calls. A few where I could have died or been paralyzed. I’ve been lucky. My crew was lucky. According to the Insurance rep I spoke to ladders are considered the most dangerous tool on any job site.
One of my first electrical jobs was adapting an electrical system for a quadriplegic who fell off a simple six-foot ladder and snapped his neck while taking down Christmas lights. He could move his head and his right thumb a bit. Serious business.
Safety first.
I. Hate. Ladders.
What I hate even more is having to do something on them that involves me no longer holding onto the ladder, which is about everything. I’m kind of ok climbing ladders in order to get somewhere, but only mildly. Even typing this makes my hands sweat and you don’t want sweaty hands on a ladder. We do have a collection of ladders foe various purposes: the small stepladder so i can get things out of the cupboards, the medium stepladder for most home repairs, the ordinary 4 m ladder and the staircase ladder with 4 adjustable feet so you can put it up safely on the stairs. I’m ok with the former two, but not with the latter two.
This dislike extends to stairs without good steps and handrails and mostly going downwards. Back in the olden times when you could visit all parts of the Sagrada Familia in Barcelona by just showing up and paying a few bucks, I went there with some friends from school. The view from the tower was spectacular. Then I noticed that I had to go down again. I sent my friends ahead and then went down on my ass like a three years old.
Pierce R. Butler@#27:
How did you clean that gutter Before Ladder, and why did you change now?
There were 15 years of accumulation up there – because that was the first time the gutter got clean-out. I was hoping it wouldn’t be an issue, ever, because that high and at the angle where it is, there isn’t much that can blow up there. But I finally had to act when I saw a small tree growing from the gutter…
Could you attach something to your drone to clean gutters with your feet &/or butt securely on the ground?
I don’t think drones are powerful enough, and I’m not that good a pilot. I suppose I could drone up a hose and try a hose cleanout, but – the ladder seemed better, for all that I hate them and they scare me.
lorn@#30:
A ladder that goes to, or in the case of roof access (the top at least 3′ above the roof deck), your best anchor is usually to get a rope over the roof and tied off on the ground on the opposite side of the house. A lot of contractors tie off to vehicles.
That’s a good idea. I considered it but when I audited my rope collection, I didn’t have enough. If I ever do this again, I will put a rope over the roof. There’s a porch on the other side with lots of beams. I just need some umpty-lb test. Getting a rope over ought to be pretty easy, he said with hope.
If I just had to do it myself I might rent a crawler bucket. They are a bigger thing now on job sites.
I checked with the rental place in Clearfield. They aren’t cheap (which is OK) but they are “tow it yourself” which would mean resurrecting the tow hitch on my Tahoe, and doing all that. The big problem, though, is that the whole mess is on a pretty steep slope. Digging a hole to put the higher leg in was easy (and made the ladder more stable) but I don’t think I could get a cherry-picker up there unless I went with one of the 4×4 ones.
Re #29: Fiddling to make it a function of distance from fixed end of ladder, x. Using sin(θ) = h/d, cos(θ) = x/d, and d² = x² + h², force required at distance x is
(mgL/2)·x/(x² + h²)
If you plot this for reasonable values of L (length of ladder) and h (height of Marcus?), with x going from L to zero, it looks a lot like the plot Marcus drew.
OK Phun with Physics (™) aside, the practical question is, Why’n’hell don’t you hire somebody to clean your gutters? Seriously, the pro services are fast & cheap (probably cheaper than that ladder).
Just an Organic Regular Expression@#35:
OK Phun with Physics (™) aside, the practical question is, Why’n’hell don’t you hire somebody to clean your gutters? Seriously, the pro services are fast & cheap (probably cheaper than that ladder).
Turns out that there aren’t any pros out here in the middle of noplace. I did call around – there are 2 places that list gutter maintenance – and was told “we don’t come out for jobs like that. But if you were to tell us we’d be installing complete new gutters, then it’d be worth it.” Basically, they need to make $1,500 or more or they can’t be arsed to load up their gear and come out. Most of the professional services are busy cleaning and maintaining stuff at well-manicured developments with 2-story high buildings that you can just drop a cherry picker off, clean it out, and load up and leave in 20 minutes. As noted, my gutter was a job and a half.
Marcus
I just had a roofer use a dummy launcher (the type used to train retriever dogs)
to get a safety rope over my 3+ story house. Brilliant!
I don’t mind being on the ladder, as long as it is very stable and secure. Six years of gymnast training comes in handy for keeping your weight centered on a small rung.
I can’t do the dead lift portion, so I generally walk it up the wall in the shortest position, then I can extend and position it incrementally.
Extender arms are a great accessory if you plan to spend much time working from the top. Braces that can clamp to an upper story window sill are also good to secure tall shaky extension ladders, assuming you have windows.
I’ve also seen the extension legs for working on slopes, but they never seem particularly stable. Maybe you could weld up something that could spike into to the ground to provide a level surface? It is critical to stay vertical. I feel nervous just reading about all that sideways sliding.
For what it is worth my Physics professor friend says there have been a lot of great explanations. It is all over my head. Now if you want to discuss history and politics, I can chime in.
Marcus Ranum @ # 32: I suppose I could drone up a hose and try a hose cleanout…
Huh – working out the amount of lift needed to raise a water-full hose to gutter level, plus withstanding the kickback force of a blast strong enough to remove a tightly-packed wad of leaf accumulation, sounds like a job for Rob Grigjanis. In any case, it would certainly require more oomph from your drone than carrying a cam, or even dragging a gutter-width mini-rake along the length of the eave several times with high precision.
Howsomever, maybe you could rig one of those high-voltage battery-powered blowers under one of the larger model drones, angled so that it wouldn’t slam the drone into the gable when you turned on the power … nah, you’d probably get only a few cubic inches of leaf-wad loosened up before the whole Rube Goldbergery blew itself away.
Since you seem to have the ladder already in place, perhaps you should look at installing some of the various Leaf-Gard®™© screenings that promise to reduce such problems, so that maybe you won’t have to do all that again until you’re old ‘n’ frail.
I concur with Giliell @ 31. I also hate ladders and I hate working from them. I can do it at home on a stepladder, but I’m afraid of falling. Besides it is illegal here (Finland) to employ another person to carry out any work from a leaning ladder. Stepladders are legal for occasional short-term work that doesn’t require using much strength on heights less than 2 m. Otherwise, a scaffolding needs to be built or an aerial work platform used.
As for going down stairs, it is hazardous (easy to trip) and hard on the knees (as anyone with knee pain may have noticed). I knew some people who would deliver newspapers in apartment blocks, climbing up the stairs and taking the lift/elevator (if available, a significant number of older 4-6 floor buildings didn’t have them) down to save their knees, back when I did that job.
One can easily extract from the mathematics the following result: if the ladder is longer than twice your (support) height, then the largest force you need to exert is the ladder’s weight times 1/4 of the ratio between the ladder’s length and the support height.
(This is assuming the ladder’s center of gravity is half-way along. If not, the numbers will vary somewhat.)
So if the ladder is 40ft and you’re holding it (to make the numbers round) at 5ft above ground level (so the ratio is 8), then (at the 45° point) you need to exert a force equal to twice the ladder’s weight.