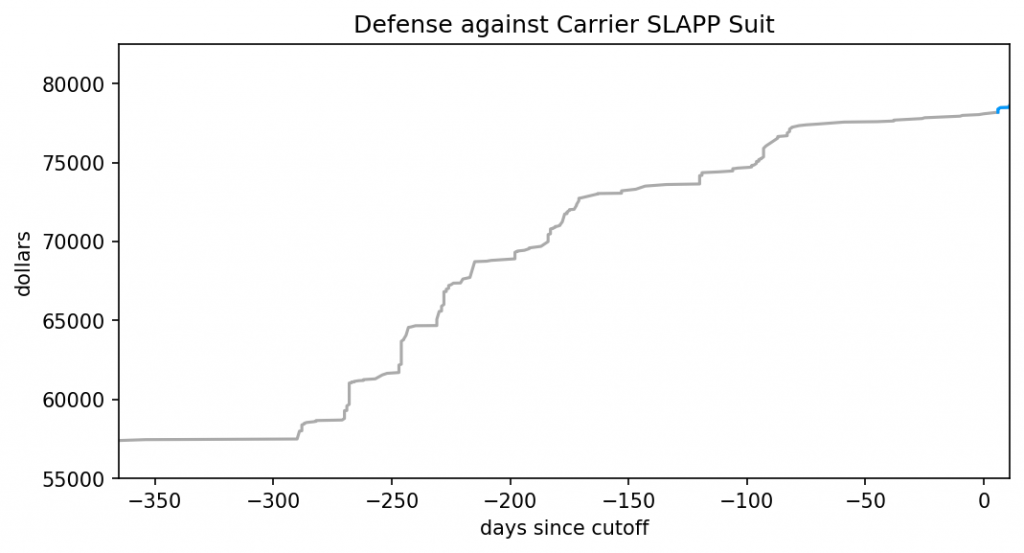
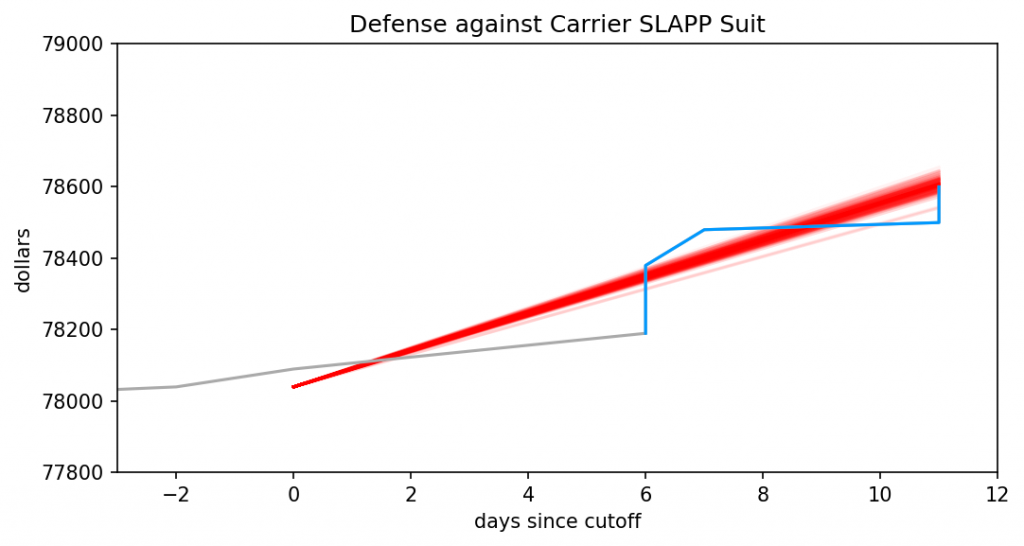
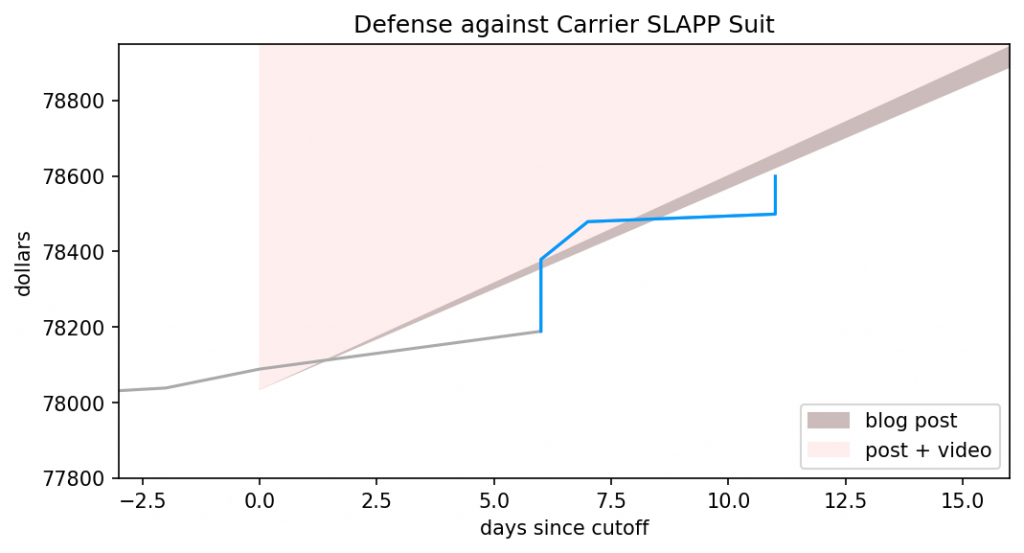
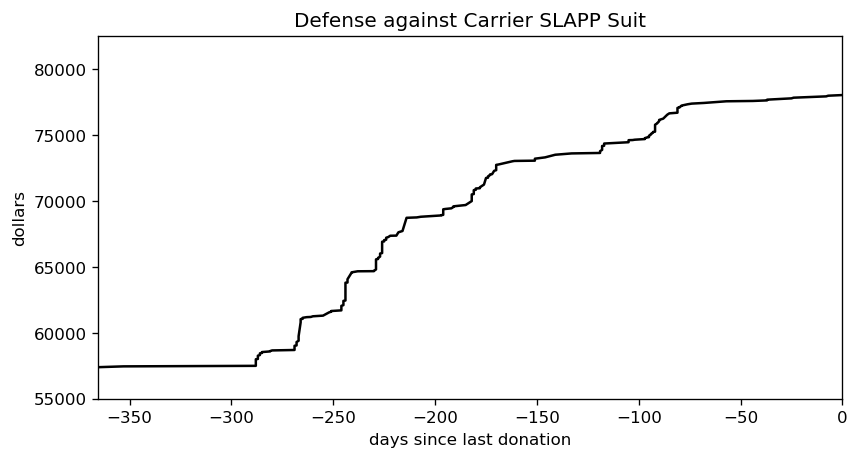
I’ve outlined how LLMs work, how they differ from Markov chains but also what they have in common. I’ve demonstrated that commonality, in great detail and with graphs. For the third and final part, I apply those previous two to a series of posts by Ranum and whip up a holiday feast for everyone.