[Content Warning: TERFs, high-level discussion of violence and sexual assault, math.]
[Content Warning: TERFs, high-level discussion of violence and sexual assault, math.]
Sorry, sorry, got lost in my day job for a bit there. It’s been a month since the fundraising deadline passed, though, and I owe you some follow-up. So, the big question: did we hit the fundraising goal? Let’s load the dataset to find out. [Read more…]
TL;DR: We’re pretty much on track, though we also haven’t hit the goal of pushing the fund past $78,890.69. Donate and help put the fund over the line!
With the short version out of the way, let’s dive into the details. What’s changed in the past week and change?
import datetime as dt
import matplotlib.pyplot as pl
import pandas as pd
import pandas.tseries.offsets as pdto
cutoff_day = dt.datetime( 2020, 5, 27, tzinfo=dt.timezone(dt.timedelta(hours=-6)) )
donations = pd.read_csv('donations.cleaned.tsv',sep='\t')
donations['epoch'] = pd.to_datetime(donations['created_at'])
donations['delta_epoch'] = donations['epoch'] - cutoff_day
donations['delta_epoch_days'] = donations['delta_epoch'].apply(lambda x: x.days)
# some adjustment is necessary to line up with the current total
donations['culm'] = donations['amount'].cumsum() + 14723
new_donations_mask = donations['delta_epoch_days'] > 0
print( f"There have been {sum(new_donations_mask)} donations since {cutoff_day}." )There have been 8 donations since 2020-05-27 00:00:00-06:00.
There’s been a reasonable number of donations after I published that original post. What does that look like, relative to the previous graph?
pl.figure(num=None, figsize=(8, 4), dpi=150, facecolor='w', edgecolor='k')
pl.plot( donations['delta_epoch_days'], donations['culm'], '-',c='#aaaaaa')
pl.plot( donations['delta_epoch_days'][new_donations_mask], \
donations['culm'][new_donations_mask], '-',c='#0099ff')
pl.title("Defense against Carrier SLAPP Suit")
pl.xlabel("days since cutoff")
pl.ylabel("dollars")
pl.xlim( [-365.26,donations['delta_epoch_days'].max()] )
pl.ylim( [55000,82500] )
pl.show()That’s certainly an improvement in the short term, though the graph is much too zoomed out to say more. Let’s zoom in, and overlay the posterior.
# load the previously-fitted posterior
flat_chain = np.loadtxt('starting_posterior.csv')
pl.figure(num=None, figsize=(8, 4), dpi=150, facecolor='w', edgecolor='k')
x = np.array([0, donations['delta_epoch_days'].max()])
for m,_,_ in flat_chain:
pl.plot( x, m*x + 78039, '-r', alpha=0.05 )
pl.plot( donations['delta_epoch_days'], donations['culm'], '-', c='#aaaaaa')
pl.plot( donations['delta_epoch_days'][new_donations_mask], \
donations['culm'][new_donations_mask], '-', c='#0099ff')
pl.title("Defense against Carrier SLAPP Suit")
pl.xlabel("days since cutoff")
pl.ylabel("dollars")
pl.xlim( [-3,x[1]+1] )
pl.ylim( [77800,79000] )
pl.show()Hmm, looks like we’re right where the posterior predicted we’d be. My targets were pretty modest, though, consisting of an increase of 3% and 10%, so this doesn’t mean they’ve been missed. Let’s extend the chart to day 16, and explicitly overlay the two targets I set out.
low_target = 78890.69
high_target = 78948.57
target_day = dt.datetime( 2020, 6, 12, 23, 59, tzinfo=dt.timezone(dt.timedelta(hours=-6)) )
target_since_cutoff = (target_day - cutoff_day).days
pl.figure(num=None, figsize=(8, 4), dpi=150, facecolor='w', edgecolor='k')
x = np.array([0, target_since_cutoff])
pl.fill_between( x, [78039, low_target], [78039, high_target], color='#ccbbbb', label='blog post')
pl.fill_between( x, [78039, high_target], [high_target, high_target], color='#ffeeee', label='video')
pl.plot( donations['delta_epoch_days'], donations['culm'], '-',c='#aaaaaa')
pl.plot( donations['delta_epoch_days'][new_donations_mask], \
donations['culm'][new_donations_mask], '-',c='#0099ff')
pl.title("Defense against Carrier SLAPP Suit")
pl.xlabel("days since cutoff")
pl.ylabel("dollars")
pl.xlim( [-3, target_since_cutoff] )
pl.ylim( [77800,high_target] )
pl.legend(loc='lower right')
pl.show()To earn a blog post and video on Bayes from me, we need the line to be in the pink zone by the time it reaches the end of the graph. For just the blog post, it need only be in the grayish- area. As you can see, it’s painfully close to being in line with the lower of two goals, though if nobody donates between now and Friday it’ll obviously fall quite short.
So if you want to see that blog post, get donating!
If our goal is to raise funds for a good cause, we should at least have an idea of where the funds are at.
import matplotlib.pyplot as pl
import pandas as pd
import pandas.tseries.offsets as pdto
donations = pd.read_csv('donations.cleaned.tsv',sep='\t')
donations['epoch'] = pd.to_datetime(donations['created_at'])
donations['delta_epoch'] = donations['epoch'] - donations['epoch'].max()
# some adjustment is necessary to line up with the current total
donations['culm'] = donations['amount'].cumsum() + (78039 - donations['amount'].sum())
donations.head()| created_at | amount | epoch | delta_epoch | culm | |
|---|---|---|---|---|---|
| 0 | 2017-01-24T07:27:51-06:00 | 10.0 | 2017-01-24 07:27:51-06:00 | -1218 days +19:51:12 | 14733.0 |
| 1 | 2017-01-24T07:31:09-06:00 | 50.0 | 2017-01-24 07:31:09-06:00 | -1218 days +19:54:30 | 14783.0 |
| 2 | 2017-01-24T07:41:20-06:00 | 100.0 | 2017-01-24 07:41:20-06:00 | -1218 days +20:04:41 | 14883.0 |
| 3 | 2017-01-24T07:50:20-06:00 | 10.0 | 2017-01-24 07:50:20-06:00 | -1218 days +20:13:41 | 14893.0 |
| 4 | 2017-01-24T08:03:26-06:00 | 25.0 | 2017-01-24 08:03:26-06:00 | -1218 days +20:26:47 | 14918.0 |
Changing the dataset so the last donation happens at time zero makes it both easier to fit the data and easier to understand what’s happening. The first day after the last donation is now day one.
Donations from 2017 don’t tell us much about the current state of the fund, though, so let’s focus on just the last year.
pl.figure(num=None, figsize=(8, 4), dpi=120, facecolor='w', edgecolor='k')
pl.plot(donations['delta_epoch'].apply(lambda x: x.days),donations['culm'],'-k')
pl.title("Defense against Carrier SLAPP Suit")
pl.xlabel("days since last donation")
pl.ylabel("dollars")
pl.xlim( [-365.26,0] )
pl.ylim( [55000,82500] )
pl.show()The donations seem to arrive in bursts, but there have been two quiet portions. One is thanks to the current pandemic, and the other was during last year’s late spring/early summer. It’s hard to tell what the donation rate is just by eye-ball, though. We need to smooth this out via a model.
The simplest such model is linear regression, aka. fitting a line. We want to incorporate uncertainty into the mix, which means a Bayesian fit. Now, what MCMC engine to use, hmmm…. emcee is my overall favourite, but I’m much too reliant on it. I’ve used PyMC3 a few times with success, but recently it’s been acting flaky. Time to pull out the big guns: Stan. I’ve been avoiding it because pystan‘s compilation times drove me nuts, but all the cool kids have switched to cmdstanpy when I looked away. Let’s give that a whirl.
import cmdstanpy as csp
%time success = csp.install_cmdstan()
if success:
print("CmdStan installed.")CPU times: user 5.33 ms, sys: 7.33 ms, total: 12.7 ms Wall time: 421 ms CmdStan installed.
We can’t fit to the entire three-year time sequence, that just wouldn’t be fair given the recent slump in donations. How about the last six months? That covers both a few donation burts and a flat period, so it’s more in line with what we’d expect in future.
mask = (donations['delta_epoch'].apply(lambda x: x.days) > -365.26*.5) # roughly six months
x = donations['delta_epoch'].apply(lambda x: x.days)[mask] # make the current time zero, for convenience
y = donations['culm'][mask]
yerr = donations['amount'].min() * .5 # the minimum donation amount adds some intrinsic uncertainty
print( f"There were {sum(mask)} donations over the last six months." )There were 117 donations over the last six months.
With the data prepped, we can shift to building the linear model.
with open('linear_regression.stan','wt') as file:
file.write("""
/* tweaked version of https://mc-stan.org/docs/2_23/stan-users-guide/linear-regression.html */
data {
int N;
vector[N] x;
vector[N] y;
real y_err;
}
parameters {
real slope;
real intercept;
real sigma;
}
model {
slope ~ cauchy( 0, 0.357369 ); /* approximate the inverse tangent prior */
/* intercept has a flat prior */
sigma ~ cauchy( 0, 1 ); /* prior that favours lower values */
/* fatter tails to reduce the influence of outliers */
y ~ student_t( 3, intercept + slope*x, sigma );
}
""") I could have just gone with Stan’s basic model, but flat priors aren’t my style. My preferred prior for the slope is the inverse tangent, as it compensates for the tendency of large slope values to “bunch up” on one another. Stan doesn’t offer it by default, but the Cauchy distribution isn’t too far off.
We’d like the standard deviation to skew towards smaller values. It naturally tends to minimize itself when maximizing the likelihood, but an explicit skew will encourage this process along. Gelman and the Stan crew are drifting towards normal priors, but I still like a Cauchy prior for its weird properties.
Normally I’d plunk the Gaussian distribution in to handle divergence from the deterministic model, but I hear using Student’s T instead will cut down the influence of outliers. Thomas Wiecki recommends one degree of freedom, but Gelman and co. find that it leads to poor convergence in some cases. They recommend somewhere between three and seven degrees of freedom, but skew towards three, so I’ll go with the flow here.
The y-intercept could land pretty much anywhere, making its prior difficult to figure out. Yes, I’ve adjusted the time axis so that the last donation is at time zero, but the recent flat portion pretty much guarantees the y-intercept will be higher than the current amount of funds. The traditional approach is to use a flat prior for the intercept, and I can’t think of a good reason to ditch that.
Not convinced I picked good priors? That’s cool, there should be enough data here that the priors have minimal influence anyway. Moving on, let’s see how long compilation takes.
%time lr_model = csp.CmdStanModel(stan_file='linear_regression.stan')CPU times: user 4.91 ms, sys: 5.3 ms, total: 10.2 ms Wall time: 20.2 s
This is one area where emcee really shines: as a pure python library, it has zero compilation time. Both PyMC3 and Stan need some time to fire up an external compiler, which adds overhead. Twenty seconds isn’t too bad, though, especially if it leads to quick sampling times.
%time lr_model_fit = lr_model.sample( data = {'N':len(x), 'x':list(x), 'y':list(y), 'y_err':yerr}, \
iter_warmup = 936, iter_sampling = 64 )CPU times: user 14.7 ms, sys: 24.7 ms, total: 39.4 ms Wall time: 829 ms
And it does! emcee can be pretty zippy for a simple linear regression, but Stan is in another class altogether. PyMC3 floats somewhere between the two, in my experience.
Another great feature of Stan are the built-in diagnostics. These are really handy for confirming the posterior converged, and if not it can give you tips on what’s wrong with the model.
print( lr_model_fit.diagnose() )Processing csv files: /tmp/tmpyfx91ua9/linear_regression-202005262238-1-e393mc6t.csv, /tmp/tmpyfx91ua9/linear_regression-202005262238-2-8u_r8umk.csv, /tmp/tmpyfx91ua9/linear_regression-202005262238-3-m36dbylo.csv, /tmp/tmpyfx91ua9/linear_regression-202005262238-4-hxjnszfe.csv Checking sampler transitions treedepth. Treedepth satisfactory for all transitions. Checking sampler transitions for divergences. No divergent transitions found. Checking E-BFMI - sampler transitions HMC potential energy. E-BFMI satisfactory for all transitions. Effective sample size satisfactory. Split R-hat values satisfactory all parameters. Processing complete, no problems detected.
The odds of a simple model with plenty of datapoints going sideways are pretty small, so this is another non-surprise. Enough waiting, though, let’s see the fit in action. First, we need to extract the posterior from the stored variables …
lr_model_names = { v:i for i,v in enumerate(lr_model_fit.column_names) }
flat_chain = list()
for sample in lr_model_fit.sample:
for chain in sample:
flat_chain.append( [chain[i] for i in map(lambda x: lr_model_names[x], ['slope', 'intercept', 'sigma'] )] )
print( f"There are {len(flat_chain)} samples in the posterior." )There are 256 samples in the posterior.
… and now free of its prison, we can plot the posterior against the original data. I’ll narrow the time window slightly, to make it easier to focus on the fit.
pl.figure(num=None, figsize=(8, 4), dpi=120, facecolor='w', edgecolor='k')
pl.plot(donations['delta_epoch'].apply(lambda x: x.days),donations['culm'],'-k')
for m,b,_ in flat_chain:
pl.plot( x, m*x + b, '-r', alpha=0.05 )
pl.title("Defense against Carrier SLAPP Suit, with linear fit")
pl.xlabel("time, days since last donation")
pl.ylabel("fund, dollars")
pl.xlim( [-365.26*.75, 0] )
pl.ylim( [55000,82500] )
pl.show()Looks like a decent fit to me, so we can start using it to answer a few questions. How much money is flowing into the fund each day, on average? How many years will it be until all those legal bills are paid off? Since humans aren’t good at counting in years, let’s also translate that number into a specific date.
import numpy as np
print( f"mean/std/median slope = ${np.mean(flat_chain,axis=0)[0]:.2f}/" + \
f"{np.std(flat_chain,axis=0)[0]:.2f}/{np.median(flat_chain,axis=0)[0]:.2f} per day")
print()
est_years = list()
est_day = list()
numer = 115000 - donations['culm'].max()
for m,b,_ in flat_chain:
target = numer/m
est_day.append( target )
est_years.append( target / 365.26 )
print( f"mean/std/median years to pay off the legal fees, relative to {donations['epoch'].max()} =" )
print( f"\t{np.mean(est_years):.3f}/{np.std(est_years):.3f}/{np.median(est_years):.3f}" )
print()
print( "mean/median estimate for paying off debt =" )
print( f"\t{donations['epoch'].max() + pdto.DateOffset(days=np.mean(est_day))} / " +
f"{donations['epoch'].max() + pdto.DateOffset(days=np.median(est_day))}" )mean/std/median slope = $51.62/1.65/51.76 per day mean/std/median years to pay off the legal fees, relative to 2020-05-25 12:36:39-05:00 = 1.962/0.063/1.955 mean/median estimate for paying off debt = 2022-05-12 07:49:55.274942-05:00 / 2022-05-09 13:57:13.461426-05:00
Mid-May 2022, eh? That’s… not ideal. How much time can we shave off, if we increase the donation rate? Let’s play out a few scenarios.
for imp in [.01,.03,.1,.3,1.]:
est_imp = list()
numer = 115000 - donations['culm'].max()
offset = donations['epoch'].max().timestamp()/86400
for m,_,_ in flat_chain:
denom = m * (1+imp)
est_imp.append( numer/denom + offset )
print( f"median estimate for paying off debt, increasing rate by {imp*100.:3.0f}% = " +
f"{pd.Timestamp(np.median(est_imp),unit='d')}" )median estimate for paying off debt, increasing rate by 1% = 2022-05-02 17:16:37.476652800 median estimate for paying off debt, increasing rate by 3% = 2022-04-18 23:48:28.185868800 median estimate for paying off debt, increasing rate by 10% = 2022-03-05 21:00:48.510403200 median estimate for paying off debt, increasing rate by 30% = 2021-11-26 00:10:56.277984 median estimate for paying off debt, increasing rate by 100% = 2021-05-17 18:16:56.230752
Bumping up the donation rate by one percent is pitiful. A three percent increase will almost shave off a month, which is just barely worthwhile, and a ten percent increase will roll the date forward by two. Those sound like good starting points, so let’s make them official: increase the current donation rate by three percent, and I’ll start pumping out the aforementioned blog posts on Bayesian statistics. Manage to increase it by 10%, and I’ll also record them as videos.
As implied, I don’t intend to keep the same rate throughout this entire process. If you surprise me with your generosity, I’ll bump up the rate. By the same token, though, if we go through a dry spell I’ll decrease the rate so the targets are easier to hit. My goal is to have at least a 50% success rate on that lower bar. Wouldn’t that make it impossible to hit the video target? Remember, though, it’ll take some time to determine the success rate. That lag should make it possible to blow past the target, and by the time this becomes an issue I’ll have thought of a better fix.
Ah, but over what timeframe should this rate increase? We could easily blow past the three percent target if someone donates a hundred bucks tomorrow, after all, and it’s no fair to announce this and hope your wallets are ready to go in an instant. How about… sixteen days. You’ve got sixteen days to hit one of those rate targets. That’s a nice round number, for a computer scientist, and it should (hopefully!) give me just enough time to whip up the first post. What does that goal translate to, in absolute numbers?
inc = 0.03
days = 16
start = donations['culm'].max()
delta = np.median(flat_chain,axis=0)[0] * (1.+inc)*days
print( f"a {inc*100.:3.0f}% increase over {days} days translates to" +
f" ${delta:.2f} + ${start:.2f} = ${start + delta:.2f}" )a 3% increase over 16 days translates to $851.69 + $78039.00 = $78890.69
Right, if you want those blog posts to start flowing you’ve got to get that fundraiser total to $78,890.69 before June 12th. As for the video…
inc = 0.1
delta = np.median(flat_chain,axis=0)[0] * (1.+inc)*days
print( f"a {inc*100.:3.0f}% increase over {days} days translates to" +
f" ${delta:.2f} + ${start:.2f} = ${start + delta:.2f}" )a 10% increase over 16 days translates to $909.57 + $78039.00 = $78948.57
… you’ve got to hit $78,948.57 by the same date.
Ready? Set? Get donating!
I’ll admit, this fundraiser isn’t exactly twisting my arm. I’ve been mulling over how I’d teach Bayesian statistics for a few years. Overall, I’ve been most impressed with E.T. Jaynes’ approach, which draws inspiration from Cox’s Theorem. You’ll see a lot of similarities between my approach and Jaynes’, though I diverge on a few points. [Read more…]
Hello! I’ve been a fan of your work for some time. While I’ve used emcee more and currently use a lot of PyMC3, I love the layout of Stan‘s language and often find myself missing it.
But there’s no contradiction between being a fan and critiquing your work. And one of your recent blog posts left me scratching my head.
Suppose I want to estimate my chances of winning the lottery by buying a ticket every day. That is, I want to do a pure Monte Carlo estimate of my probability of winning. How long will it take before I have an estimate that’s within 10% of the true value?
This one’s pretty easy to set up, thanks to conjugate priors. The Beta distribution models our credibility of the odds of success from a Bernoulli process. If our prior belief is represented by the parameter pair \((\alpha_\text{prior},\beta_\text{prior})\), and we win \(w\) times over \(n\) trials, our posterior belief in the odds of us winning the lottery, \(p\), is
$$ \begin{align}
\alpha_\text{posterior} &= \alpha_\text{prior} + w, \\
\beta_\text{posterior} &= \beta_\text{prior} + n – w
\end{align} $$
You make it pretty clear that by “lottery” you mean the traditional kind, with a big payout that your highly unlikely to win, so \(w \approx 0\). But in the process you make things much more confusing.
There’s a big NY state lottery for which there is a 1 in 300M chance of winning the jackpot. Back of the envelope, to get an estimate within 10% of the true value of 1/300M will take many millions of years.
“Many millions of years,” when we’re “buying a ticket every day?” That can’t be right. The mean of the Beta distribution is
$$ \begin{equation}
\mathbb{E}[Beta(\alpha_\text{posterior},\beta_\text{posterior})] = \frac{\alpha_\text{posterior}}{\alpha_\text{posterior} + \beta_\text{posterior}}
\end{equation} $$
So if we’re trying to get that within 10% of zero, and \(w = 0\), we can write
$$ \begin{align}
\frac{\alpha_\text{prior}}{\alpha_\text{prior} + \beta_\text{prior} + n} &< \frac{1}{10} \\
10 \alpha_\text{prior} &< \alpha_\text{prior} + \beta_\text{prior} + n \\
9 \alpha_\text{prior} – \beta_\text{prior} &< n
\end{align} $$
If we plug in a sensible-if-improper subjective prior like \(\alpha_\text{prior} = 0, \beta_\text{prior} = 1\), then we don’t even need to purchase a single ticket. If we insist on an “objective” prior like Jeffrey’s, then we need to purchase five tickets. If for whatever reason we foolishly insist on the Bayes/Laplace prior, we need nine tickets. Even at our most pessimistic, we need less than a fortnight (or, if you prefer, much less than a Fortnite season). If we switch to the maximal likelihood instead of the mean, the situation gets worse.
$$ \begin{align}
\text{Mode}[Beta(\alpha_\text{posterior},\beta_\text{posterior})] &= \frac{\alpha_\text{posterior} – 1}{\alpha_\text{posterior} + \beta_\text{posterior} – 2} \\
\frac{\alpha_\text{prior} – 1}{\alpha_\text{prior} + \beta_\text{prior} + n – 2} &< \frac{1}{10} \\
9\alpha_\text{prior} – \beta_\text{prior} – 8 &< n
\end{align} $$
Now Jeffrey’s prior doesn’t require us to purchase a ticket, and even that awful Bayes/Laplace prior needs just one purchase. I can’t see how you get millions of years out of that scenario.
Maybe you meant a different scenario, though. We often use credible intervals to make decisions, so maybe you meant that the entire interval has to pass below the 0.1 mark? This introduces another variable, the width of the credible interval. Most people use two standard deviations or thereabouts, but I and a few others prefer a single standard deviation. Let’s just go with the higher bar, and start hacking away at the variance of the Beta distribution.
$$ \begin{align}
\text{var}[Beta(\alpha_\text{posterior},\beta_\text{posterior})] &= \frac{\alpha_\text{posterior}\beta_\text{posterior}}{(\alpha_\text{posterior} + \beta_\text{posterior})^2(\alpha_\text{posterior} + \beta_\text{posterior} + 2)} \\
\sigma[Beta(\alpha_\text{posterior},\beta_\text{posterior})] &= \sqrt{\frac{\alpha_\text{prior}(\beta_\text{prior} + n)}{(\alpha_\text{prior} + \beta_\text{prior} + n)^2(\alpha_\text{prior} + \beta_\text{prior} + n + 2)}} \\
\frac{\alpha_\text{prior}}{\alpha_\text{prior} + \beta_\text{prior} + n} + \frac{2}{\alpha_\text{prior} + \beta_\text{prior} + n} \sqrt{\frac{\alpha_\text{prior}(\beta_\text{prior} + n)}{\alpha_\text{prior} + \beta_\text{prior} + n + 2}} &< \frac{1}{10}
\end{align} $$
Our improper subjective prior still requires zero ticket purchases, as \(\alpha_\text{prior} = 0\) wipes out the entire mess. For Jeffrey’s prior, we find
$$ \begin{equation}
\frac{\frac{1}{2}}{n + 1} + \frac{2}{n + 1} \sqrt{\frac{1}{2}\frac{n + \frac 1 2}{n + 3}} < \frac{1}{10},
\end{equation} $$
which needs 18 ticket purchases according to Wolfram Alpha. The awful Bayes/Laplace prior can almost get away with 27 tickets, but not quite. Both of those stretch the meaning of “back of the envelope,” but you can get the answer via a calculator and some trial-and-error.
I used the term “hacking” for a reason, though. That variance formula is only accurate when \(p \approx \frac 1 2\) or \(n\) is large, and neither is true in this scenario. We’re likely underestimating the number of tickets we’d need to buy. To get an accurate answer, we need to integrate the Beta distribution.
$$ \begin{align}
\int_{p=0}^{\frac{1}{10}} \frac{\Gamma(\alpha_\text{posterior} + \beta_\text{posterior})}{\Gamma(\alpha_\text{posterior})\Gamma(\beta_\text{posterior})} p^{\alpha_\text{posterior} – 1} (1-p)^{\beta_\text{posterior} – 1} > \frac{39}{40} \\
40 \frac{\Gamma(\alpha_\text{prior} + \beta_\text{prior} + n)}{\Gamma(\alpha_\text{prior})\Gamma(\beta_\text{prior} + n)} \int_{p=0}^{\frac{1}{10}} p^{\alpha_\text{prior} – 1} (1-p)^{\beta_\text{prior} + n – 1} > 39
\end{align} $$
Awful, but at least for our subjective prior it’s trivial to evaluate. \(\text{Beta}(0,n+1)\) is a Dirac delta at \(p = 0\), so 100% of the integral is below 0.1 and we still don’t need to purchase a single ticket. Fortunately for both the Jeffrey’s and Bayes/Laplace prior, my “envelope” is a Jupyter notebook.
from mpmath import mp
mp.dps = 20 # set the desired precision
def eval_integral_one(alpha, beta, n, limit=0.1):
return mp.gammaprod([alpha + beta + n],[alpha, beta + n]) * \
mp.quad(lambda p: p**(alpha-1)*(1-p)**(beta+n-1), [0, limit])
def find_n(alpha, beta, limit=0.1, threshold=0.975):
output = list()
n = 0
while True:
output.append( eval_integral_one(alpha,beta,n,limit=limit) )
if output[-1] > threshold:
break
else:
n += 1
return output
y_jefferys = find_n( .5,.5 )
y_bayes = find_n( 1, 1 )
import matplotlib.pyplot as plt
plt.figure( figsize=(8,4), dpi=96 )
plt.plot( range(len(y_jefferys)), y_jefferys, '-k', label="Jeffrey's prior")
plt.plot( range(len(y_bayes)), y_bayes, '-g', label="Bayes/Laplace prior")
plt.xlabel('n')
plt.xticks( [0, len(y_jefferys), len(y_bayes)] )
plt.ylabel('Beta(α,β) < 1/10')
plt.yticks( [0.25,0.5,0.975] )
plt.legend()
plt.show()Those numbers did go up by a non-trivial amount, but we’re still nowhere near “many millions of years,” even if Fortnite’s last season felt that long.
Maybe you meant some scenario where the credible interval overlaps \(p = 0\)? With proper priors, that never happens; the lower part of the credible interval always leaves room for some extremely small values of \(p\), and thus never actually equals 0. My sensible improper prior has both ends of the interval equal to zero and thus as long as \(w = 0\) it will always overlap \(p = 0\).
I think I can find a scenario where you’re right, but I also bet you’re sick of me calling \((0,1)\) a “sensible” subjective prior. Hope you don’t mind if I take a quick detour to the last question in that blog post, which should explain how a Dirac delta can be sensible.
How long would it take to convince yourself that playing the lottery has an expected negative return if tickets cost $1, there’s a 1/300M chance of winning, and the payout is $100M?
Let’s say the payout if you win is \(W\) dollars, and the cost of a ticket is \(T\). Then your expected earnings at any moment is an integral of a multiple of the entire Beta posterior.
$$ \begin{equation}
\mathbb{E}(\text{Lottery}_{W}) = \int_{p=0}^1 \frac{\Gamma(\alpha_\text{posterior} + \beta_\text{posterior})}{\Gamma(\alpha_\text{posterior})\Gamma(\beta_\text{posterior})} p^{\alpha_\text{posterior} – 1} (1-p)^{\beta_\text{posterior} – 1} p W < T
\end{equation} $$
I’m pretty confident you can see why that’s a back-of-the-envelope calculation, but this is a public letter and I’m also sure some of those readers just fainted. Let me detour from the detour to assure them that, yes, this is actually a pretty simple calculation. They’ve already seen that multiplicative constants can be yanked out of the integral, but I’m not sure they realized that if
$$ \begin{equation}
\int_{p=0}^1 \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)} p^{\alpha – 1} (1-p)^{\beta – 1} = 1,
\end{equation} $$
then thanks to the multiplicative constant rule it must be true that
$$ \begin{equation}
\int_{p=0}^1 p^{\alpha – 1} (1-p)^{\beta – 1} = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha + \beta)}
\end{equation} $$
They may also be unaware that the Gamma function is an analytic continuity of the factorial. I say “an” because there’s an infinite number of functions that also qualify. To be considered a “good” analytic continuity the Gamma function must also duplicate another property of the factorial, that \((a + 1)! = (a + 1)(a!)\) for all valid \(a\). Or, put another way, it must be true that
$$ \begin{equation}
\frac{\Gamma(a + 1)}{\Gamma(a)} = a + 1, a > 0
\end{equation} $$
Fortunately for me, the Gamma function is a good analytic continuity, perhaps even the best. This allows me to chop that integral down to size.
$$ \begin{align}
W \frac{\Gamma(\alpha_\text{prior} + \beta_\text{prior} + n)}{\Gamma(\alpha_\text{prior})\Gamma(\beta_\text{prior} + n)} \int_{p=0}^1 p^{\alpha_\text{prior} – 1} (1-p)^{\beta_\text{prior} + n – 1} p &< T \\
\int_{p=0}^1 p^{\alpha_\text{prior} – 1} (1-p)^{\beta_\text{prior} + n – 1} p &= \int_{p=0}^1 p^{\alpha_\text{prior}} (1-p)^{\beta_\text{prior} + n – 1} \\
\int_{p=0}^1 p^{\alpha_\text{prior}} (1-p)^{\beta_\text{prior} + n – 1} &= \frac{\Gamma(\alpha_\text{prior} + 1)\Gamma(\beta_\text{prior} + n)}{\Gamma(\alpha_\text{prior} + \beta_\text{prior} + n + 1)} \\
W \frac{\Gamma(\alpha_\text{prior} + \beta_\text{prior} + n)}{\Gamma(\alpha_\text{prior})\Gamma(\beta_\text{prior} + n)} \frac{\Gamma(\alpha_\text{prior} + 1)\Gamma(\beta_\text{prior} + n)}{\Gamma(\alpha_\text{prior} + \beta_\text{prior} + n + 1)} &< T \\
W \frac{\Gamma(\alpha_\text{prior} + \beta_\text{prior} + n) \Gamma(\alpha_\text{prior} + 1)}{\Gamma(\alpha_\text{prior} + \beta_\text{prior} + n + 1) \Gamma(\alpha_\text{prior})} &< T \\
W \frac{\alpha_\text{prior} + 1}{\alpha_\text{prior} + \beta_\text{prior} + n + 1} &< T \\
\frac{W}{T}(\alpha_\text{prior} + 1) – \alpha_\text{prior} – \beta_\text{prior} – 1 &< n
\end{align} $$
Mmmm, that was satisfying. Anyway, for Jeffrey’s prior you need to purchase \(n > 149,999,998\) tickets to be convinced this lottery isn’t worth investing in, while the Bayes/Laplace prior argues for \(n > 199,999,997\) purchases. Plug my subjective prior in, and you’d need to purchase \(n > 99,999,998\) tickets.
That’s optimal, assuming we know little about the odds of winning this lottery. The number of tickets we need to purchase is controlled by our prior. Since \(W \gg T\), our best bet to minimize the number of tickets we need to purchase is to minimize \(\alpha_\text{prior}\). Unfortunately, the lowest we can go is \(\alpha_\text{prior} = 0\). Almost all the “objective” priors I know of have it larger, and thus ask that you sink more money into the lottery than the prize is worth. That doesn’t sit well with our intuition. The sole exception is the Haldane prior of (0,0), which argues for \(n > 99,999,999\) and thus asks you to spend exactly as much as the prize-winnings. By stating \(\beta_\text{prior} = 1\), my prior manages to shave off one ticket purchase.
Another prior that increases \(\beta_\text{prior}\) further will shave off further purchases, but so far we’ve only considered the case where \(w = 0\). What if we sink money into this lottery, and happen to win before hitting our limit? The subjective prior of \((0,1)\) after \(n\) losses becomes equivalent to the Bayes/Laplace prior of \((1,1)\) after \(n-1\) losses. Our assumption that \(p \approx 0\) has been proven wrong, so the next best choice is to make no assumptions about \(p\). At the same time, we’ve seen \(n\) losses and we’d be foolish to discard that information entirely. A subjective prior with \(\beta_\text{prior} > 1\) wouldn’t transform in this manner, while one with \(\beta_\text{prior} < 1\) would be biased towards winning the lottery relative to the Bayes/Laplace prior.
My subjective prior argues you shouldn’t play the lottery, which matches the reality that almost all lotteries pay out less than they take in, but if you insist on participating it will minimize your losses while still responding well to an unexpected win. It lives up to the hype.
However, there is one way to beat it. You mentioned in your post that the odds of winning this lottery are one in 300 million. We’re not supposed to incorporate that into our math, it’s just a measuring stick to use against the values we churn out, but what if we constructed a prior around it anyway? This prior should have a mean of one in 300 million, and the \(p = 0\) case should have zero likelihood. The best match is \((1+\epsilon, 299999999\cdot(1+\epsilon))\), where \(\epsilon\) is a small number, and when we take a limit …
$$ \begin{equation}
\lim_{\epsilon \to 0^{+}} \frac{100,000,000}{1}(2 + \epsilon) – 299,999,999 \epsilon – 300,000,000 = -100,000,000 < n
\end{equation} $$
… we find the only winning move is not to play. There’s no Dirac deltas here, either, so unlike my subjective prior it’s credible interval is one-dimensional. Eliminating the \(p = 0\) case runs contrary to our intuition, however. A newborn that purchased a ticket every day of its life until it died on its 80th birthday has a 99.99% chance of never holding a winning ticket. \(p = 0\) is always an option when you live a finite amount of time.
The problem with this new prior is that it’s incredibly strong. If we didn’t have the true odds of winning in our back pocket, we could quite fairly be accused of putting our thumb on the scales. We can water down \((1,299999999)\) by dividing both \(\alpha_\text{prior}\) and \(\beta_\text{prior}\) by a constant value. This maintains the mean of the Beta distribution, and while the \(p = 0\) case now has non-zero credence I’ve shown that’s no big deal. Pick the appropriate constant value and we get something like \((\epsilon,1)\), where \(\epsilon\) is a small positive value. Quite literally, that’s within epsilon of the subjective prior I’ve been hyping!
So far, the only back-of-the-envelope calculations I’ve done that argued for millions of ticket purchases involved the expected value, but that was only because we used weak priors that are a poor match for reality. I believe in the principle of charity, though, and I can see a scenario where a back-of-the-envelope calculation does demand millions of purchases.
But to do so, I’ve got to hop the fence and become a frequentist.
If you haven’t read The Theory That Would Not Die, you’re missing out. Sharon Bertsch McGrayne mentions one anecdote about the RAND Corporation’s attempts to calculate the odds of a nuclear weapon accidentally detonating back in the 1950’s. No frequentist statistician would touch it with a twenty-foot pole, but not because they were worried about getting the math wrong. The problem was the math. As the eventually-published report states:
The usual way of estimating the probability of an accident in a given situation is to rely on observations of past accidents. This approach is used in the Air Force, for example, by the Directory of Flight Safety Research to estimate the probability per flying hour of an aircraft accident. In cases of of newly introduced aircraft types for which there are no accident statistics, past experience of similar types is used by analogy.
Such an approach is not possible in a field where this is no record of past accidents. After more than a decade of handling nuclear weapons, no unauthorized detonation has occurred. Furthermore, one cannot find a satisfactory analogy to the complicated chain of events that would have to precede an unauthorized nuclear detonation. (…) Hence we are left with the banal observation that zero accidents have occurred. On this basis the maximal likelihood estimate of the probability of an accident in any future exposure turns out to be zero.
For the lottery scenario, a frequentist wouldn’t reach for the Beta distribution but instead the Binomial. Given \(n\) trials of a Bernoulli process with probability \(p\) of success, the expected number of successes observed is
$$ \begin{equation}
\bar w = n p
\end{equation} $$
We can convert that to a maximal likelihood estimate by dividing the actual number of observed successes by \(n\).
$$ \begin{equation}
\hat p = \frac{w}{n}
\end{equation} $$
In many ways this estimate can be considered optimal, as it is both unbiased and has the least variance of all other estimators. Thanks to the Central Limit Theorem, the Binomial distribution will approximate a Gaussian distribution to arbitrary degree as we increase \(n\), which allows us to apply the analysis from the latter to the former. So we can use our maximal likelihood estimate \(\hat p\) to calculate the standard error of that estimate.
$$ \begin{equation}
\text{SEM}[\hat p] = \sqrt{ \frac{\hat p(1- \hat p)}{n} }
\end{equation} $$
Ah, but what if \(w = 0\)? It follows that \(\hat p = 0\), but this also means that \(\text{SEM}[\hat p] = 0\). There’s no variance in our estimate? That can’t be right. If we approach this from another angle, plugging \(w = 0\) into the Binomial distribution, it reduces to
$$ \begin{equation}
\text{Binomial}(w | n,p) = \frac{n!}{w!(n-w)!} p^w (1-p)^{n-w} = (1-p)^n
\end{equation} $$
The maximal likelihood of this Binomial is indeed \(p = 0\), but it doesn’t resemble a Dirac delta at all.
import numpy as np
plt.figure( figsize=(8,4), dpi=96 )
n = 25 # stopping point, Jeffrey's prior
x = np.linspace(0,1,256)
plt.plot( x, (1-x)**n, '-k', label='Binomial, n={}, w=0'.format(n) )
plt.xlabel('p')
plt.xticks( [0,.5,1] )
plt.ylabel('likelihood')
plt.yticks( [] )
plt.legend()
plt.show()Shouldn’t there be some sort of variance there? What’s going wrong?
We got a taste of this on the Bayesian side of the fence. Using the stock formula for the variance of the Beta distribution underestimated the true value, because the stock formula assumed \(p \approx \frac 1 2\) or a large \(n\). When we assume we have a near-infinite amount of data, we can take all sorts of computational shortcuts that make our life easier. One look at the Binomial’s mean, however, tells us that we can drown out the effects of a large \(n\) with a small value of \(p\). And, just as with the odds of a nuclear bomb accident, we already know \(p\) is very, very small. That isn’t fatal on its own, as you correctly point out.
With the lottery, if you run a few hundred draws, your estimate is almost certainly going to be exactly zero. Did we break the [*Central Limit Theorem*]? Nope. Zero has the right absolute error properties. It’s within 1/300M of the true answer after all!
The problem comes when we apply the Central Limit Theorem and use a Gaussian approximation to generate a confidence or credible interval for that maximal likelihood estimate. As both the math and graph show, though, the probability distribution isn’t well-described by a Gaussian distribution. This isn’t much of a problem on the Bayesian side of the fence, as I can juggle multiple priors and switch to integration for small values of \(n\). Frequentism, however, is dependent on the Central Limit Theorem and thus assumes \(n\) is sufficiently large. This is baked right into the definitions: a p-value is the fraction of times you calculate a test metric equal to or more extreme than the current one assuming the null hypothesis is true and an infinite number of equivalent trials of the same random process, while confidence intervals are a range of parameter values such that when we repeat the maximal likelihood estimate on an infinite number of equivalent trials the estimates will fall in that range more often than a fraction of our choosing. Frequentist statisticians are stuck with the math telling them that \(p = 0\) with absolute certainty, which conflicts with our intuitive understanding.
For a frequentist, there appears to be only one way out of this trap: witness a nuclear bomb accident. Once \(w > 0\), the math starts returning values that better match intuition. Likewise with the lottery scenario, the only way for a frequentist to get an estimate of \(p\) that comes close to their intuition is to purchase tickets until they win at least once.
This scenario does indeed take “many millions of years.” It’s strange to find you taking a frequentist world-view, though, when you’re clearly a Bayesian. By straddling the fence you wind up in a world of hurt. For instance, you state this:
Did we break the [*Central Limit Theorem*]? Nope. Zero has the right absolute error properties. It’s within 1/300M of the true answer after all! But it has terrible relative error probabilities; it’s relative error after a lifetime of playing the lottery is basically infinity.
A true frequentist would have been fine asserting the probability of a nuclear bomb accident is zero. Why? Because \(\text{SEM}[\hat p = 0]\) is actually a very good confidence interval. If we’re going for two sigmas, then our confidence interval should contain the maximal likelihood we’ve calculated at least 95% of the time. Let’s say our sample sizes are \(n = 36\), the worst-case result from Bayesian statistics. If the true odds of winning the lottery are 1 in 300 million, then the odds of calculating a maximal likelihood of \(p = 0\) is
print("p( MLE(hat p) = 0 ) = ", ((299999999)**36) / ((300000000)**36) )p( MLE(hat p) = 0 ) = 0.999999880000007
About 99.99999% of the time, then, the confidence interval of \(0 \leq \hat p \leq 0\) will be correct. That’s substantially better than 95%! Nothing’s broken here, frequentism is working exactly as intended.
I bet you think I’ve screwed up the definition of confidence intervals. I’m afraid not, I’ve double-checked my interpretation by heading back to the source, Jerzy Neyman. He, more than any other person, is responsible for pioneering the frequentist confidence interval.
We can then tell the practical statistician that whenever he is certain that the form of the probability law of the X’s is given by the function? \(p(E|\theta_1, \theta_2, \dots \theta_l,)\) which served to determine \(\underline{\theta}(E)\) and \(\bar \theta(E)\) [the lower and upper bounds of the confidence interval], he may estimate \(\theta_1\) by making the following three steps: (a) he must perform the random experiment and observe the particular values \(x_1, x_2, \dots x_n\) of the X’s; (b) he must use these values to calculate the corresponding values of \(\underline{\theta}(E)\) and \(\bar \theta(E)\); and (c) he must state that \(\underline{\theta}(E) < \theta_1^o < \bar \theta(E)\), where \(\theta_1^o\) denotes the true value of \(\theta_1\). How can this recommendation be justified?
[Neyman keeps alternating between \(\underline{\theta}(E) \leq \theta_1^o \leq \bar \theta(E)\) and \(\underline{\theta}(E) < \theta_1^o < \bar \theta(E)\) throughout this paper, so presumably both forms are A-OK.]
The justification lies in the character of probabilities as used here, and in the law of great numbers. According to this empirical law, which has been confirmed by numerous experiments, whenever we frequently and independently repeat a random experiment with a constant probability, \(\alpha\), of a certain result, A, then the relative frequency of the occurrence of this result approaches \(\alpha\). Now the three steps (a), (b), and (c) recommended to the practical statistician represent a random experiment which may result in a correct statement concerning the value of \(\theta_1\). This result may be denoted by A, and if the calculations leading to the functions \(\underline{\theta}(E)\) and \(\bar \theta(E)\) are correct, the probability of A will be constantly equal to \(\alpha\). In fact, the statement (c) concerning the value of \(\theta_1\) is only correct when \(\underline{\theta}(E)\) falls below \(\theta_1^o\) and \(\bar \theta(E)\), above \(\theta_1^o\), and the probability of this is equal to \(\alpha\) whenever \(\theta_1^o\) the true value of \(\theta_1\). It follows that if the practical statistician applies permanently the rules (a), (b) and (c) for purposes of estimating the value of the parameter \(\theta_1\) in the long run he will be correct in about 99 per cent of all cases. […]
It will be noticed that in the above description the probability statements refer to the problems of estimation with which the statistician will be concerned in the future. In fact, I have repeatedly stated that the frequency of correct results tend to \(\alpha\). [Footnote: This, of course, is subject to restriction that the X’s considered will follow the probability law assumed.] Consider now the case when a sample, E’, is already drawn and the calculations have given, say, \(\underline{\theta}(E’)\) = 1 and \(\bar \theta(E’)\) = 2. Can we say that in this particular case the probability of the true value of \(\theta_1\) falling between 1 and 2 is equal to \(\alpha\)?
The answer is obviously in the negative. The parameter \(\theta_1\) is an unknown constant and no probability statement concerning its value may be made, that is except for the hypothetical and trivial ones … which we have decided not to consider.
Neyman, Jerzy. “X — outline of a theory of statistical estimation based on the classical theory of probability.” Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 236.767 (1937): 348-349.
If there was any further doubt, it’s erased when Neyman goes on to analogize scientific measurements to a game of roulette. Just as the knowing where the ball landed doesn’t tell us anything about where the gamblers placed their bets, “once the sample \(E’\) is drawn and the values of \(\underline{\theta}(E’)\) and \(\bar \theta(E’)\) determined, the calculus of probability adopted here is helpless to provide answer to the question of what is the true value of \(\theta_1\).” (pg. 350)
If a confidence interval doesn’t tell us anything about where the true parameter value lies, then its only value must come from being an estimator of long-term behaviour. And as I showed before, \(\text{SEM}[\hat p = 0]\) estimates the maximal likelihood from repeating the experiment extremely well. It is derived from the long-term behaviour of the Binomial distribution, which is the correct distribution to describe this situation within frequentism. \(\text{SEM}[\hat p = 0]\) fits Neyman’s definition of a confidence interval perfectly, and thus generates a valid frequentist confidence interval. On the Bayesian side, I’ve spilled a substantial number of photons to convince you that a Dirac delta prior is a good choice, and that prior also generates zero-width credence intervals. If it worked over there, why can’t it also work over here?
This is Jayne’s Truncated Interval all over again. The rules of frequentism don’t work the way we intuit, which normally isn’t a problem because the Central Limit Theorem massages the data enough to align frequentism and intuition. Here, though, we’ve stumbled on a corner case where \(p = 0\) with absolute certainty and \(p \neq 0\) with tight error bars are both correct conclusions under the rules of frequentism. RAND Corporation should not have had any difficulty finding a frequentist willing to calculate the odds of a nuclear bomb accident, because they could have scribbled out one formula on an envelope and concluded such accidents were impossible.
And yet, faced with two contradictory answers or unaware the contradiction exists, frequentists side with intuition and reject the rules of their own statistical system. They strike off the \(p = 0\) answer, leaving only the case where \(p \ne 0\) and \(w > 0\). Since reality currently insists that \(w = 0\), they’re prevented from coming to any conclusion. The same reasoning leads to the “many millions of years” of ticket purchases that you argued was the true back-of-the-envelope conclusion. To break out of this rut, RAND Corporation was forced to abandon frequentism and instead get their estimate via Bayesian statistics.
On this basis the maximal likelihood estimate of the probability of an accident in any future exposure turns out to be zero. Obviously we cannot rest content with this finding. […]
… we can use the following idea: in an operation where an accident seems to be possible on technical grounds, our assurance that this operation will not lead to an accident in the future increases with the number of times this operation has been carried out safely, and decreases with the number of times it will be carried out in the future. Statistically speaking, this simple common sense idea is based on the notion that there is an a priori distribution of the probability of an accident in a given opportunity, which is not all concentrated at zero. In Appendix II, Section 2, alternative forms for such an a priori distribution are discussed, and a particular Beta distribution is found to be especially useful for our purposes.
It’s been said that frequentists are closet Bayesians. Through some misunderstandings and bad luck on your end, you’ve managed to be a Bayesian that’s a closet frequentist that’s a closet Bayesian. Had you stuck with a pure Bayesian view, any back-of-the-envelope calculation would have concluded that your original scenario demanded, in the worst case, that you’d need to purchase lottery tickets for a Fortnite.
I’m trying something new! This blog post is available in two places, both here and on a Jupyter notebook. Over there, you can tweak and execute my source code, using it as a sandbox for your own explorations. Over here, it’s just a boring ol’ webpage without any fancy features, albeit one that’s easier to read on the go. Choose your own adventure!
Oh also, CONTENT WARNING: I’ll briefly be discussing sexual assault statistics from the USA at the start, in an abstract sense.
[5:08] Now this might seem pedantic to those not interested in athletics, but in the athletic world one percent is absolutely massive. Just take for example the 2016 Olympics. The difference between first and second place in the men’s 100-meter sprint was 0.8%.
I’ve covered this argument from Rationality Rules before, but time has made me realise my original presentation had a problem.
His name is Steven Pinker.
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
assault = pd.read_csv('https://gitlab.com/hjhornbeck/texas_sharpshooter/raw/master/data/pinker_rape_usa.tsv',sep='\t')
plt.rcParams['figure.dpi'] = 96
plt.rcParams['figure.figsize'] = [9.5, 6]
plt.plot( assault['# Year'], assault['Rate'], 'b' )
plt.title('Forcible Rape, USA, Police reports')
plt.xlabel('Year')
plt.ylabel('Rate per 100,000')
plt.show()
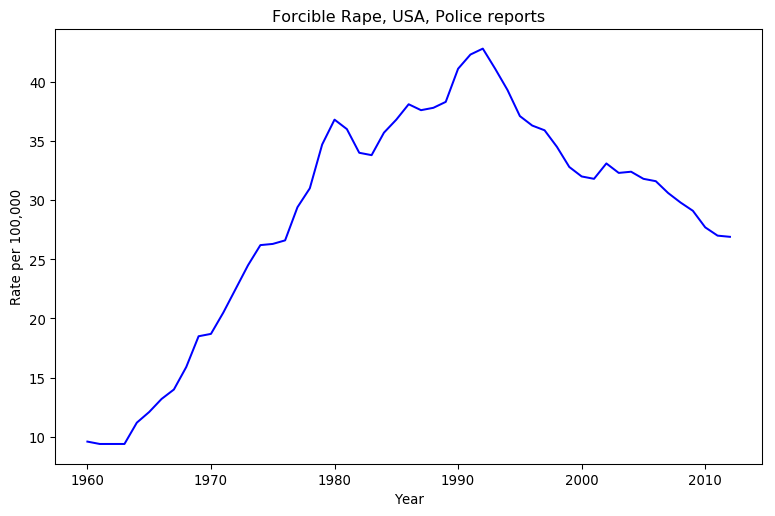 He looks at that graph, and sees a decline in violence. I look at that chart, and see an increase in violence. How can two people look at the same data, and come to contradictory conclusions?
He looks at that graph, and sees a decline in violence. I look at that chart, and see an increase in violence. How can two people look at the same data, and come to contradictory conclusions?
Simple, we’ve got at least two separate mental models.
import emcee
import numpy as np
import os
import scipy.optimize as spop
# Some of this code is based on the following examples:
# https://emcee.readthedocs.io/en/v2.2.1/user/line/
# https://jakevdp.github.io/blog/2014/06/14/frequentism-and-bayesianism-4-bayesian-in-python/
def lnLinear( theta, x, y ):
intercept, slope, lnStdDev = theta
prior = -1.5*np.log1p(slope*slope) - lnStdDev
model = slope*x + intercept
inv_sig2 = 1. / (model**2 * np.exp(2*lnStdDev))
return prior - .5*( np.sum( ((y-model)**2) * inv_sig2 - np.log(inv_sig2) ) )
# Model 1: What's happened over the last two decades?
negLnLin = lambda *args: -lnLinear(*args)
max_year = np.max( assault['# Year'] )
start = 1991
end = max_year
mask = assault['# Year'] > start
print("Finding the maximal likelihood, please wait ...", end='')
intercept_1, slope_1, error_1 = spop.minimize( negLnLin, [1000,-1,5],
args=(assault['# Year'][mask], assault['Rate'][mask]) )['x']
print(" done.")
# Model 2: Where are the extremes?
min_year = np.min( assault['# Year'] )
slope_2 = (float(assault['Rate'][assault['# Year']==max_year]) - float(assault['Rate'][assault['# Year']==min_year])) / \
(max_year - min_year)
intercept_2 = float(assault['Rate'][assault['# Year']==min_year] - slope_2*min_year)
# Model 3: What trendlines fit the data?
ndim, nwalkers, nsamples, keep = 3, 64, 300, 1
seed = [np.array([intercept_2,slope_2,3.]) + 1e-4*np.random.randn(ndim) for i in range(nwalkers)]
sampler = emcee.EnsembleSampler(nwalkers, ndim, lnLinear, threads=os.cpu_count(),
args=[ np.array(assault['# Year']), np.array(assault['Rate']) ] )
print("Running an MCMC sampler, please wait ...", end='')
sampler.run_mcmc(seed, nsamples)
print(" done.")
model_3 = sampler.chain[:, -keep:, :].reshape((-1, ndim))
print("Charting the results, please wait ...")
plt.plot( assault['# Year'], assault['Rate'], 'k' )
plt.xlabel('Year')
plt.ylabel('Rate per 100,000')
plt.plot( assault['# Year'], slope_1*assault['# Year'] + intercept_1, 'r' )
plt.plot( assault['# Year'], slope_2*assault['# Year'] + intercept_2, 'g' )
for entry in model_3:
plt.plot( assault['# Year'], entry[1]*assault['# Year'] + entry[0], 'b', alpha=0.05 )
plt.legend( ['Original Data', 'Model 1 (Pinker)', 'Model 2 (Mine)', 'Model 3 (Mine)'])
plt.show()
Finding the maximal likelihood, please wait ... done. Running an MCMC sampler, please wait ... done. Charting the results, please wait ...
All Pinker cares about is short-term trends here, as he’s focused on “The Great Decline” in crime since the 1990’s. His mental model looks at the general trend over the last two decades of data, and discards the rest of the datapoints. It’s the model I’ve put in red.
I used two seperate models in my blog post. The first is quite crude: is the last datapoint better than the first? This model is quite intuitive, as it amounts to “leave the place in better shape than when you arrived,” and it’s dead easy to calculate. It discards all but two datapoints, though, which is worse than Pinker’s model. I’ve put this one in green.
The best model, in my opinion, wouldn’t discard any datapoints. It would also incorporate as much uncertainty as possible about the system. Unsurprisingly, given my blogging history, I consider Bayesian statistics to be the best way to represent uncertainty. A linear model is the best choice for general trends, so I went with a three-parameter likelihood and prior:
This third model encompasses all possible trendlines you could draw on the graph, but it doesn’t hold them all to be equally likely. Since time is short, I used an MCMC sampler to randomly sample the resulting probability distribution, and charted that sample in blue. As you can imagine this requires a lot more calculation than the second model, but I can’t think of anything superior.
Which model is best depends on the context. If you were arguing just over the rate of police-reported sexual assault from 1992 to 2012, Pinker’s model would be pretty good if incomplete. However, his whole schtick is that long-term trends show a decrease in violence, and when it comes to sexual violence in particular he’s the only one who dares to talk about this. He’s not being self-consistent, which is easier to see when you make your implicit mental models explicit.
Let’s return to Rationality Rules’ latest transphobic video. In the citations, he explicitly references the men’s 100m sprint at the 2016 Olympics. That’s a terribly narrow window to view athletic performance through, so I tracked down the racetimes of all eight finalists on the IAAF’s website and tossed them into a spreadsheet.
dataset = pd.read_csv('https://gitlab.com/hjhornbeck/texas_sharpshooter/raw/master/data/100_metre.tsv',delimiter='\t',parse_dates=[1],dayfirst=True,dtype={'Result':np.float64,'Wind':np.float64})
olympics_2016 = dataset['Competition'] == "Rio de Janeiro Olympic Games"
finals = dataset['Race'] == "F"
fastest_time = min(dataset['Result'][olympics_2016 & finals])
table = {"Athlete":dataset['# Name'][olympics_2016 & finals],
"Result":dataset['Result'][olympics_2016 & finals],
"Delta":dataset['Result'][olympics_2016 & finals] - fastest_time
}
print("Rio de Janeiro Olympic Games, finals")
print( pd.DataFrame(table).sort_values("Result").to_string(index=False) )
Rio de Janeiro Olympic Games, finals
Athlete Result Delta
bolt 9.81 0.00
gatlin 9.89 0.08
de grasse 9.91 0.10
blake 9.93 0.12
simbine 9.94 0.13
meite 9.96 0.15
vicaut 10.04 0.23
bromell 10.06 0.25
Here, we see exactly what Rationality Rules sees: Usain Bolt, the current world record holder, earned himself another Olympic gold medal in the 100m sprint. First and third place are separated by a tenth of a second, and the slowest person in the finals was a mere quarter of a second behind the fastest. That’s a small fraction of the time it takes to complete the event.
mask_2016 = (dataset['Date'] > '2016-01-01') & (dataset['Date'] < '2017-01-01')
names_2016 = pd.Categorical( dataset['# Name'] ).categories
all_2016 = list()
for name in names_2016:
temp = np.array( dataset['Result'][mask_2016 & (dataset['# Name'] == name)] )
temp.sort()
all_2016.append( temp )
all_career = list()
for name in names_2016:
all_career.append( np.max( dataset['Date'][dataset['# Name'] == name] ) - np.min( dataset['Date'][dataset['# Name'] == name] ) )
all_races = list()
for name in names_2016:
all_races.append( len( dataset['Result'][dataset['# Name'] == name] ) )
mean_time = sorted( np.linspace(0,len(all_2016)-1,len(all_2016),dtype=int), key=lambda x:np.mean(all_2016[x]))
median_time = sorted( np.linspace(0,len(all_2016)-1,len(all_2016),dtype=int), key=lambda x:np.median(all_2016[x]))
min_time = sorted( np.linspace(0,len(all_2016)-1,len(all_2016),dtype=int), key=lambda x:np.min(all_2016[x]))
fastest_time = np.min([ np.min(data) for data in all_2016 ])
print('Race times in 2016, sorted by fastest time')
print("{0:16} {1:16} {2:16} {3:16} {4:16}".format('Name','Min time', 'Mean', 'Median', 'Personal max-min'))
print("{}".format( '-' * (6*16 + 5) ))
for i in min_time:
print("{0:16} {1:16} {2:12.2f} {3:12.2f} {4:12.2f}".format( names_2016[i], np.min(all_2016[i]), np.mean(all_2016[i]),
np.median(all_2016[i]), np.max(all_2016[i]) - np.min(all_2016[i]) ))
Race times in 2016, sorted by fastest time Name Min time Mean Median Personal max-min ----------------------------------------------------------------------------------------------------- gatlin 9.8 9.95 9.94 0.39 bolt 9.81 9.98 10.01 0.34 bromell 9.84 10.00 10.01 0.30 vicaut 9.86 10.01 10.02 0.33 simbine 9.89 10.10 10.08 0.43 de grasse 9.91 10.07 10.04 0.41 blake 9.93 10.04 9.98 0.33 meite 9.95 10.10 10.05 0.44
Here, we see what I see: the person who won Olympic gold that year didn’t have the fastest time. That honour goes to Justin Gatlin, who squeaked ahead of Bolt by a hundredth of a second.
Come to think of it, isn’t the fastest time a poor judge of how good an athlete is? Picture one sprinter with a faster average time than another, and a second with a faster minimum time. The first athlete will win more races than the second. By that metric, Gatlin’s lead grows to three hundredths of a second.
The mean, alas, is easily tugged around by outliers. If someone had an exceptionally good or bad race, they could easily shift their overall mean a decent ways from where the mean of every other result lies. The median is a lot more resistant to the extremes, and thus a fairer measure of overall performance. By that metric, Bolt is now tied for third with Trayvon Bromell.
We could also judge how good an athlete is by how consistent they were in the given calendar year. By this metric, Bolt falls into fourth place behind Bromell, Jimmy Vicaut, and Yohan Blake. Even if you don’t agree to this metric, notice how everyone’s race times in 2016 varies between three and four tenths of a second. It’s hard to argue that a performance edge of a tenth of a second matters when even at the elite level sprinters’ times will vary by significantly more.
But let’s put on our Steven Pinker glasses. We don’t judge races by medians, we go by the fastest time. We don’t award records for the lowest average or most consistent performance, we go by the fastest time. Yes, Bolt didn’t have the fastest 100m time in 2016, but now we’re down to hundredths of a second; if anything, we’ve dug up more evidence that itty-bitty performance differences matter. If I’d just left things at that last paragraph, which is about as far as I progressed the argument last time, a Steven Pinker would likely have walked away even more convinced that Rationality Rules got it right.
I don’t have to leave things there, though. This time around, I’ll make my mental model as explicit as possible. Hopefully by fully arguing the case, instead of dumping out data and hoping you and I share the same mental model, I could manage to sway even a diehard skeptic. To further seal the deal, the Jupyter notebook will allow you to audit my thinking or even create your own model. No need to take my word.
I’m laying everything out in clear sight. I hope you’ll give it all a look before dismissing me.
Our choice of model will be guided by the assumptions we make about how athletes perform in the 100 metre sprint. If we’re going to do this properly, we have to lay out those assumptions as clearly as possible.
Based on all the above, I propose the Gamma distribution would make a suitable model.
(Be careful not to confuse the distribution with the function. I may need the Gamma function to calculate the Gamma distribution, but the Gamma function isn’t a valid probability distribution.)
import scipy.stats as spst
x = np.linspace(0,10,1023)
print("Three versions of the Gamma Distribution")
plt.subplot( 131 )
plt.plot( x, spst.gamma.pdf(x, 5, scale=.7) )
plt.xticks([0])
plt.yticks([])
plt.xlabel('"Canonical"')
plt.subplot( 132 )
plt.plot( x, spst.gamma.pdf(x, 1, scale=2) )
plt.xticks([0])
plt.yticks([])
plt.xlabel('Exponential')
plt.subplot( 133 )
plt.plot( x, spst.gamma.pdf(x, 200, scale=.025) )
plt.xticks([0])
plt.yticks([])
plt.xlabel('pseudo-Gaussian')
plt.show()
Three versions of the Gamma Distribution
It’s a remarkably flexible distribution, capable of duplicating both the Exponential and Gaussian distributions. That’s handy, as if one of our above assumptions is wrong the fitting process could still come up with a good fit. Note that the Gamma distribution has a finite bound at zero, which is equivalent to stating that negative values are impossible. The variance can be expanded or contracted arbitrarily, so it isn’t implicitly supporting my arguments. Best of all, we’re not restricted to anchor the distribution at zero. With a little tweak …
… we can shift that zero mark wherever we wish. The parameter sets the minimum value our model predicts, while α controls the underlying shape and β controls the scale or rate associated with this distribution. α < 1 nets you the Exponential, and large values of α lead to something very Gaussian. Conveniently for me, SciPy already supports this three-parameter tweak.
My intuition is that the Gamma distribution on the left, with α > 1 but not too big, is the best model for athlete performance. That implies an athlete’s performance will hover around a specific value, and while they’re capable of faster times those are more difficult to pull off. The Exponential distribution, with α < 1, is most favourable to Rationality Rules, as it asserts the race time we’re most likely to observe is also the fastest time an athlete can do. We’ll never actually see that time, but what we observe will cluster around that minimum.
Enough chatter, let’s fit some models! For this one, my prior will be
which is pretty light and only exists to filter out garbage values.
import sys
def lnprob( theta, data ):
alpha, beta, b = theta
if (alpha <= 0) or (beta <= 0) or (b <= 0):
return -np.inf
return np.sum( spst.gamma.logpdf( data, alpha, scale=beta, loc=b ) )
ndim, nwalkers, nsamples, keep = 3, 64, 300, 5
models = [[] for x in all_2016]
summaries = [[] for x in all_2016]
print("Generating some models for 2016 race times (a few seconds each) ...")
print( "{:16}\t{:16}\t{:16}\t{:16}".format("# name","α","β","b") )
for loc,idx in enumerate(min_time):
data = all_2016[idx]
mean = np.mean( data ) - fastest_time # adjust for the location offset
seed = list()
i = 0
while i < nwalkers: beta = np.random.rand()*1.5 + .5 b = fastest_time - np.random.rand()*.3 if lnprob( [mean*beta, beta, b], data ) > -np.inf:
seed.append( [mean*beta, beta, b] )
i += 1
sampler = emcee.EnsembleSampler(nwalkers, ndim, lnprob, args=[data], threads=os.cpu_count())
sampler.run_mcmc(seed, nsamples)
samples = sampler.chain[:, -keep:, :].reshape((-1, ndim))
alpha_mcmc, beta_mcmc, b_mcmc = map(lambda v: (v[1], v[2]-v[1], v[1]-v[0]),
zip(*np.percentile(samples, [16, 50, 84], axis=0)))
print("{:16}".format(names_2016[idx]), end='')
print("\t{:.3f} (+{:.3f} -{:.3f})".format(*alpha_mcmc), end='')
print("\t{:.3f} (+{:.3f} -{:.3f})".format(*beta_mcmc), end='')
print("\t{:.3f} (+{:.3f} -{:.3f})".format(*b_mcmc))
sys.stdout.flush()
models[idx] = samples
summaries[idx] = [*alpha_mcmc, *beta_mcmc, *b_mcmc]
print("... done.")
Generating some models for 2016 race times (a few seconds each) ... # name α β b gatlin 0.288 (+0.112 -0.075) 1.973 (+0.765 -0.511) 9.798 (+0.002 -0.016) bolt 0.310 (+0.107 -0.083) 1.723 (+0.596 -0.459) 9.802 (+0.008 -0.025) bromell 0.339 (+0.115 -0.082) 1.677 (+0.570 -0.404) 9.836 (+0.004 -0.032) vicaut 0.332 (+0.066 -0.084) 1.576 (+0.315 -0.400) 9.856 (+0.004 -0.013) simbine 0.401 (+0.077 -0.068) 1.327 (+0.256 -0.226) 9.887 (+0.003 -0.018) de grasse 0.357 (+0.073 -0.082) 1.340 (+0.274 -0.307) 9.907 (+0.003 -0.022) blake 0.289 (+0.103 -0.085) 1.223 (+0.437 -0.361) 9.929 (+0.001 -0.008) meite 0.328 (+0.089 -0.067) 1.090 (+0.295 -0.222) 9.949 (+0.000 -0.003) ... done.
This text can’t change based on the results of the code, so this is only a guess, but I’m pretty sure you’re seeing a lot of α values less than one. That really had me worried when I first ran this model, as I was already conceding ground to Rationality Rules by focusing only on the 100 metre sprint, where even I think that physiology plays a significant role. I did a few trial runs with a prior that forced α > 1, but the resulting models would hug that threshold as tightly as possible. Comparing likelihoods, the α < 1 versions were always more likely than the α > 1 ones.
The fitting process was telling me my intuition was wrong, and the best model here is the one that most favours Rationality Rules. Look at the b values, too. There’s no way I could have sorted the models based on that parameter before I fit them; instead, I sorted them by each athlete’s minimum time. Sure enough, the model is hugging the fastest time each athlete posted that year, rather than a hypothetical minimum time they could achieve.
athlete = 0
x = np.linspace(9.5,11,300)
for i,row in enumerate(models[athlete]):
if i < 100:
plt.plot( x, spst.gamma.pdf(x, row[0], scale=row[1], loc=row[2]), alpha=0.05, color='k' )
else:
break
plt.yticks([])
plt.yscale('log')
plt.ylabel('log(likelihood)')
plt.title("100 models of {}'s 2016 race times".format(names_2016[athlete]))
plt.show()
Charting some of the models in the posterior drives this home. I’ve looked at a few by tweaking the “player” variable, as well as the output of multiple sample runs, and they all are dominated by Exponential distributions.
Dang, we’ve tilted the playing field quite a ways in Rationality Rules’ favour.
Still, let’s simulate some races. For each race, I’ll pick a random trio of parameters from each model’s posterior and feet that into SciPy’s random number routines to generate a race time for each sprinter. Fastest time wins, and we tally up those wins to estimate the odds of any one sprinter coming in first.
Before running those simulations, though, we should make some predictions. Rationality Rules’ view is that (emphasis mine) …
[9:18] You see, I absolutely understand why we have and still do categorize sports based upon sex, as it’s simply the case that the vast majority of males have significant athletic advantages over females, but strictly speaking it’s not due to their sex. It’s due to factors that heavily correlate with their sex, such as height, width, heart size, lung size, bone density, muscle mass, muscle fiber type, hemoglobin, and so on. Or, in other words, sports are not segregated due to chromosomes, they’re segregated due to morphology.
[16:48] Which is to say that the attributes granted from male puberty that play a vital role in explosive events – such as height, width, limb length, and fast twitch muscle fibers – have not been shown to be sufficiently mitigated by HRT in trans women.
[19:07] In some events – such as long-distance running, in which hemoglobin and slow-twitch muscle fibers are vital – I think there’s a strong argument to say no, [transgender women who transitioned after puberty] don’t have an unfair advantage, as the primary attributes are sufficiently mitigated. But in most events, and especially those in which height, width, hip size, limb length, muscle mass, and muscle fiber type are the primary attributes – such as weightlifting, sprinting, hammer throw, javelin, netball, boxing, karate, basketball, rugby, judo, rowing, hockey, and many more – my answer is yes, most do have an unfair advantage.
… human morphology due to puberty is the primary determinant of race performance. Since our bodies change little after puberty, that implies your race performance should be both constant and consistent. The most extreme version of this argument states that the fastest person should win 100% of the time. I doubt Rationality Rules holds that view, but I am pretty confident he’d place the odds of the fastest person winning quite high.
The opposite view is that the winner is due to chance. Since there are eight athletes competing here, each would have a 12.5% chance of winning. I certainly don’t hold that view, but I do argue that chance plays a significant role in who wins. I thus want the odds of the fastest person winning to be somewhere above 12.8%, but not too much higher.
simulations = 15000
wins = [0] * len(all_2016)
print("Simulating {} races, please wait ...".format(simulations), end='')
for sim in range(simulations):
times = list()
for athlete,_ in enumerate(all_2016):
choice = int( np.random.rand()*len(models[athlete]) )
times.append( models[athlete][choice][2] + np.random.gamma( models[athlete][choice][0], models[athlete][choice][1] ) )
wins[ np.argmin(times) ] += 1
print(" done.")
by_wins = sorted( np.linspace(0,len(all_2016)-1,len(all_2016),dtype=int), key=lambda x: wins[x], reverse=True)
print()
print("Number of wins during simulation")
print("--------------------------------")
for i,athlete in enumerate(by_wins):
print( "{:24} {:8} ({:.2f}%)".format(names_2016[athlete], wins[athlete], wins[athlete]*100./simulations) )
sys.stdout.flush()
Simulating 15000 races, please wait ... done. Number of wins during simulation -------------------------------- gatlin 5174 (34.49%) bolt 4611 (30.74%) bromell 2286 (15.24%) vicaut 1491 (9.94%) simbine 530 (3.53%) de grasse 513 (3.42%) blake 278 (1.85%) meite 117 (0.78%)
Whew! The fastest 100 metre sprinter of 2016 only had a one in three chance of winning Olympic gold. Of the eight athletes, three had odds better than chance of winning. Even with the field tilted in favor of Rationality Rules, this strongly hints that other factors are more determinative of performance than fixed physiology.
But let’s put our Steven Pinker glasses back on for a moment. Yes, the odds of the fastest 100 metre sprinter winning the 2016 Olympics are surprisingly low, but look at the spread between first and last place. What’s on my screen tells me that Gatlin is 40-50 times more likely to win Olympic gold than Ben Youssef Meite, which is a pretty substantial gap. Maybe we can rescue Rationality Rules?
In order for Meite to win, though, he didn’t just have to beat Gatlin. He had to also beat six other sprinters. If pM represents the geometric mean of Meite beating one sprinter, then his odds of beating seven are pM7. The same rationale applies to Gatlin, of course, but because the geometric mean of him beating seven other racers is higher than pM, repeatedly multiplying it by itself results in a much greater number. With a little math, we can use the number of wins above to estimate how well the first-place finisher would fare against the last-place finisher in a one-on-one race.
win_ratio = float(np.max(wins)) / float(np.min(wins))
prob_head2head = np.power( win_ratio, 1./7. ) / (1 + np.power( win_ratio, 1./7. ))
print("In the above simulation, {} was {:.1f} times more likely to win Olympic gold than {}.".format(
names_2016[by_wins[0]], win_ratio, names_2016[by_wins[-1]] ))
print("But we estimate that if they were racing head-to-head,", end='')
print(" {} would win only {:.1f}% of the time.".format( names_2016[by_wins[0]], prob_head2head*100. ))
difference = (np.min(all_2016[by_wins[-1]]) - np.min(all_2016[by_wins[0]])) / np.min(all_2016[by_wins[0]])
print(" (For reference, their best race times in 2016 differed by {:.2f}%.)".format( difference * 100. ))
In the above simulation, gatlin was 39.5 times more likely to win Olympic gold than meite. But we estimate that if they were racing head-to-head, gatlin would win only 62.8% of the time. (For reference, their best race times in 2016 differed by 1.53%.)
For comparison, FiveThirtyEight gave roughly those odds for Hilary Clinton becoming the president of the USA in 2016. That’s not all that high, given how “massive” the difference is in their best race times that year.
This is just an estimate, though. Maybe if we pitted our models head-to-head, we’d get different results?
headCount = max( simulations >> 3, 100 )
maxFound = 0
print()
print("Wins when racing head to head ({} simulations each)".format( headCount ))
print("----------------------------------------------")
print("{:10}".format("LOSER->"), end='')
for _,idx in enumerate(min_time):
print("{:>10}".format(names_2016[idx]), end='')
print()
for x,x_ind in enumerate(min_time):
print("{:10}".format(names_2016[x_ind]), end='')
for y in range(len(min_time)):
if y <= x:
print("{:10}".format(""), end='')
else:
wins = 0
for rand in range(headCount):
choice = int( np.random.rand()*len(models[x_ind]) )
x_time = models[x_ind][choice][1] + np.random.gamma( models[x_ind][choice][0], models[x_ind][choice][2] )
choice = int( np.random.rand()*len(models[min_time[y]]) )
y_time = models[min_time[y]][choice][1] + np.random.gamma( models[min_time[y]][choice][0], models[min_time[y]][choice][2] )
if y_time < x_time:
wins += 1
temp = wins*100./headCount
if temp < 50: temp = 100 - temp if temp > maxFound:
maxFound = temp
print("{:9.1f}%".format(wins*100./headCount), end='')
print()
sys.stdout.flush()
print()
print("The best winning percentage was {:.1f}% (therefore the worst losing percent was {:.1f}%).".format(
maxFound, 100-maxFound ))
Wins when racing head to head (1875 simulations each) ---------------------------------------------- LOSER-> gatlin bolt bromell vicaut simbine de grasse blake meite gatlin 48.9% 52.1% 55.8% 56.4% 59.5% 63.5% 61.9% bolt 52.2% 57.9% 55.8% 57.9% 65.8% 60.2% bromell 52.4% 55.3% 55.0% 65.2% 59.0% vicaut 51.7% 52.2% 59.8% 59.3% simbine 52.3% 57.7% 57.1% de grasse 57.0% 54.7% blake 47.2% meite The best winning percentage was 65.8% (therefore the worst losing percent was 34.2%).
Nope, it’s pretty much bang on! The columns of this chart represents the loser of the head-to-head, while the rows represent the winner. That number in the upper-right, then, represents the odds of Gatlin coming in first against Meite. When I run the numbers, I usually get a percentage that’s less than 5 percentage points off. Since the odds of one person losing is the odds of the other person winning, you can flip around who won and lost by subtracting the odds from 100%. That explains why I only calculated less than half of the match-ups.
I don’t know what’s on your screen, but I typically get one or two match-ups that are below 50%. I’m again organizing the calculations by each athlete’s fastest time in 2016, so if an athlete’s win ratio was purely determined by that then every single value in this table would be equal to or above 50%. That’s usually the case, thanks to each model favouring the Exponential distribution, but sometimes one sprinter still winds up with a better average time than a second’s fastest time. As pointed out earlier, that translates into more wins for the first athlete.
Even at this elite level, you can see the odds of someone winning a head-to-head race are not terribly high. A layperson can create that much bias in a coin toss, yet we still both outcomes of that toss to be equally likely.
This doesn’t really contradict Rationality Rules’ claim that fractions of a percent in performance matter, though. Each of these athletes differ in physiology, and while that may not have as much effect as we thought it still has some effect. What we really need is a way to substract out the effects due to morphology.
If you read that old blog post, you know what’s coming next.
[16:48] Which is to say that the attributes granted from male puberty that play a vital role in explosive events – such as height, width, limb length, and fast twitch muscle fibers – have not been shown to be sufficiently mitigated by HRT in trans women.
According to Rationality Rules, the physical traits that determine track performance are all set in place by puberty. Since puberty finishes roughly around age 15, and human beings can easily live to 75, that implies those traits are fixed for most of our lifespan. In practice that’s not quite true, as (for instance) human beings lose a bit of height in old age, but here we’re only dealing with athletes in the prime of their career. Every attribute Rationality Rules lists is effectively constant.
So to truly put RR’s claim to the test, we need to fit our model to different parts of the same athlete’s career, and compare those head-to-head results with the ones where we raced athletes against each other.
table = {"Athlete":[], "First Result":[], "Latest Result":[]}
for name in names_2016:
mask_name = dataset['# Name'] == name
dates = dataset["Date"][mask_name]
table['Athlete'].append( name )
table['First Result'].append( dates.min() )
table['Latest Result'].append( dates.max() )
print( pd.DataFrame(table) )
Athlete First Result Latest Result 0 blake 2005-07-13 2019-06-21 1 bolt 2007-07-18 2017-08-05 2 bromell 2012-04-06 2019-06-08 3 de grasse 2012-06-08 2019-06-20 4 gatlin 2000-05-13 2019-07-05 5 meite 2003-07-11 2018-06-16 6 simbine 2010-03-13 2019-06-20 7 vicaut 2008-07-05 2019-07-02
That dataset contains official IAAF times going back nearly two decades, in some cases, for those eight athletes. In the case of Bolt and Meite, those span their entire sprinting career.
Which athlete should we focus on? It’s tempting to go with Bolt, but he’s an outlier who broke the mathmatical models used to predict sprint times. Gatlin would have been my second choice, but between his unusually long career and history of doping there’s a decent argument that he too is an outlier. Bromell seems free of any issue, so I’ll go with him. Don’t agree? I made changing the athlete as simple as altering one variable, so you can pick whoever you like.
I’ll divide up these athlete’s careers by year, as their performance should be pretty constant over that timespan, and for this sport there’s usually enough datapoints within the year to get a decent fit.
athlete = 2 # look at the indicies on the previous table
min_races = 3 # minimum number of races per year; filters out thin data
print()
print("{0} vs. {0}, model building ...".format( names_2016[athlete] ))
mask_ath = dataset['# Name'] == names_2016[athlete]
min_year = np.min( dataset['Date'][ mask_ath ] ).year
max_year = np.max( dataset['Date'][ mask_ath ] ).year
years = list()
models_ath = list()
summaries_ath = list()
print("year\tα\tβ\tb")
for year in range(min_year, max_year+1):
mask_year = (dataset['Date'] > '{}-01-01'.format(year)) & (dataset['Date'] < '{}-01-01'.format(year+1)) data = dataset['Result'][ mask_ath & mask_year ] if len(data) >= min_races:
years.append( year )
else:
continue
mean = np.mean( data ) - fastest_time # adjust for the bation offset
seed = list()
i = 0
while i < nwalkers: beta = np.random.rand()*1.5 + .5 b = fastest_time - np.random.rand()*.3 if lnprob( [mean*beta, beta, b], data ) > -np.inf:
seed.append( [mean*beta, beta, b] )
i += 1
sampler = emcee.EnsembleSampler(nwalkers, ndim, lnprob, args=[data], threads=os.cpu_count())
sampler.run_mcmc(seed, nsamples)
samples = sampler.chain[:, -keep:, :].reshape((-1, ndim))
alpha_mcmc, beta_mcmc, b_mcmc = map(lambda v: (v[1], v[2]-v[1], v[1]-v[0]),
zip(*np.percentile(samples, [16, 50, 84], axis=0)))
print("{}".format(year), end='')
print("\t{:.3f} (+{:.3f} -{:.3f})".format(*alpha_mcmc), end='')
print("\t{:.3f} (+{:.3f} -{:.3f})".format(*beta_mcmc), end='')
print("\t{:.3f} (+{:.3f} -{:.3f})".format(*b_mcmc))
sys.stdout.flush()
models_ath.append( samples )
summaries_ath.append( [*alpha_mcmc, *beta_mcmc, *b_mcmc] )
print("... done.")
print()
print("{0} vs. {0}, head to head ({1} simulations)".format( names_2016[athlete], headCount ))
print("----------------------------------------------")
print("{:7}".format("LOSER->"), end='')
for year in years:
print("{:>7}".format(year), end='')
print()
maxFound = 0
for x_ind,x in enumerate( years ):
print("{:7}".format(x), end='')
for y_ind,y in enumerate( years ):
if y <= x:
print("{:7}".format(""), end='')
else:
wins = 0
for rand in range(headCount):
choice = int( np.random.rand()*len(models_ath[x_ind]) )
x_time = models_ath[x_ind][choice][2] + np.random.gamma( models_ath[x_ind][choice][0], models_ath[x_ind][choice][1] )
choice = int( np.random.rand()*len(models_ath[y_ind]) )
y_time = models_ath[y_ind][choice][2] + np.random.gamma( models_ath[y_ind][choice][0], models_ath[y_ind][choice][1] )
if y_time < x_time:
wins += 1
temp = wins*100./headCount
if temp < 50: temp = 100 - temp if temp > maxFound:
maxFound = temp
print("{:6.1f}%".format(wins*100./headCount), end='')
print()
sys.stdout.flush()
print()
print("The best winning percentage was {:.1f}% (therefore the worst losing percent was {:.1f}%).".format(
maxFound, 100-maxFound ))
bromell vs. bromell, model building ... year α β b 2012 0.639 (+0.317 -0.219) 0.817 (+0.406 -0.280) 10.370 (+0.028 -0.415) 2013 0.662 (+0.157 -0.118) 1.090 (+0.258 -0.195) 9.970 (+0.018 -0.070) 2014 0.457 (+0.118 -0.070) 1.556 (+0.403 -0.238) 9.762 (+0.007 -0.035) 2015 0.312 (+0.069 -0.064) 2.082 (+0.459 -0.423) 9.758 (+0.002 -0.016) 2016 0.356 (+0.092 -0.104) 1.761 (+0.457 -0.513) 9.835 (+0.005 -0.037) ... done. bromell vs. bromell, head to head (1875 simulations) ---------------------------------------------- LOSER-> 2012 2013 2014 2015 2016 2012 61.3% 67.4% 74.3% 71.0% 2013 65.1% 70.7% 66.9% 2014 57.7% 48.7% 2015 40.2% 2016 The best winning percentage was 74.3% (therefore the worst losing percent was 25.7%).
Again, I have no idea what you’re seeing, but I’ve looked at a number of Bromell vs. Bromell runs, and every one I’ve done shows at least as much variation, if not more, than runs that pit Bromell against other athletes. Bromell vs. Bromell shows even more variation in success than the coin flip benchmark, giving us justification for saying Bromell has a significant advantage over Bromell.
I’ve also changed that variable myself, and seen the same pattern in other athletes. Worried about a lack of datapoints causing the model to “fuzz out” and cover a wide range of values? I thought of that and restricted the code to filter out years with less than three races. Honestly, I think it puts my conclusion on firmer ground.
Texas Sharpshooter Fallacy: Ignoring the difference while focusing on the similarities, thus coming to an inaccurate conclusion. Similar to the gambler’s fallacy, this is an example of inserting meaning into randomness.
Rationality Rules loves to point to sporting records and the outcome of single races, as on the surface these seem to justify his assertion that differences in performance of fractions of a percent matter. In reality, he’s painting a bullseye around a very small subset of the data and ignoring the rest. When you include all the data, you find Rationality Rules has badly missed the mark. Physiology cannot be as determinative as Rationality Rules claims, other factors must be important enough to sometimes overrule it.
And, at long last, I can call bullshit on this (emphasis mine):
[17:50] It’s important to stress, by the way, that these are just my views. I’m not a biologist, physiologist, or statistician, though I have had people check this video who are.
Either Rationality Rules found a statistician who has no idea of variance, which is like finding a computer scientist who doesn’t know boolean logic, or he never actually consulted a statistician. Chalk up yet another lie in his column.
P-values are back in the news. Nature published an article, signed by 800 scientists, calling for an end to the concept of “statistical significance.” It ruffled my feathers, even though I agreed with its central thesis.
The trouble is human and cognitive more than it is statistical: bucketing results into ‘statistically significant’ and ‘statistically non-significant’ makes people think that the items assigned in that way are categorically different. The same problems are likely to arise under any proposed statistical alternative that involves dichotomization, whether frequentist, Bayesian or otherwise.
Unfortunately, the false belief that crossing the threshold of statistical significance is enough to show that a result is ‘real’ has led scientists and journal editors to privilege such results, thereby distorting the literature. Statistically significant estimates are biased upwards in magnitude and potentially to a large degree, whereas statistically non-significant estimates are biased downwards in magnitude. Consequently, any discussion that focuses on estimates chosen for their significance will be biased. On top of this, the rigid focus on statistical significance encourages researchers to choose data and methods that yield statistical significance for some desired (or simply publishable) result, or that yield statistical non-significance for an undesired result, such as potential side effects of drugs — thereby invalidating conclusions.
Nothing wrong there. While I’ve mentioned some Bayesian buckets, I tucked away a one-sentence counter-argument in an aside over here. Any artificial significant/non-significant boundary is going to promote the distortions they mention here. What got me writing this post was their recommendations.
What will retiring statistical significance look like? We hope that methods sections and data tabulation will be more detailed and nuanced. Authors will emphasize their estimates and the uncertainty in them — for example, by explicitly discussing the lower and upper limits of their intervals. They will not rely on significance tests. When P values are reported, they will be given with sensible precision (for example, P = 0.021 or P = 0.13) — without adornments such as stars or letters to denote statistical significance and not as binary inequalities (P < 0.05 or P > 0.05). Decisions to interpret or to publish results will not be based on statistical thresholds. People will spend less time with statistical software, and more time thinking.
This basically amounts to nothing. Journal editors still have to decide what to print, and if there is no strong alternative they’ll switch from an arbitrary cutoff of p < 0.05 to an ad-hoc arbitrary cutoff. In the meantime, they’re leaving flawed statistical procedures in place. P-values exaggerate the strength of the evidence, as I and others have argued. Confidence intervals are not an improvement, either. As I put it:
For one thing, if you’re a frequentist it’s a category error to state the odds of a hypothesis being true, or that some data makes a hypothesis more likely, or even that you’re testing the truth-hood of a hypothesis. […]
How does this intersect with confidence intervals? If it’s an invalid move to hypothesise[sic] “the population mean is Y,” it must also be invalid to say “there’s a 95% chance the population mean is between X and Z.” That’s attaching a probability to a hypothesis, and therefore a no-no! Instead, what a frequentist confidence interval is really telling you is “assuming this data is a representative sample, if I repeat my experimental procedure an infinite number of times then I’ll calculate a sample mean between X and Z 95% of the time.” A confidence interval says nothing about the test statistic, at least not directly.
In frequentism, the parameter is fixed and the data varies. It doesn’t make sense to consider other parameters, that’s a Bayesian move. And yet the authors propose exactly that!
We must learn to embrace uncertainty. One practical way to do so is to rename confidence intervals as ‘compatibility intervals’ and interpret them in a way that avoids overconfidence. Specifically, we recommend that authors describe the practical implications of all values inside the interval, especially the observed effect (or point estimate) and the limits. In doing so, they should remember that all the values between the interval’s limits are reasonably compatible with the data, given the statistical assumptions used to compute the interval. Therefore, singling out one particular value (such as the null value) in the interval as ‘shown’ makes no sense.
Much of what the authors proposed would be fixed by switching to Bayesian statistics. Their own suggestions invoke Bayesian ideas without realizing it. Yet they go out of their way to say nothing’s wrong with p-values or confidence intervals, despite evidence to the contrary. Their proposal is destined to fail, yet it got more support than the arguably-superior p < 0.005 proposal.
Maddening. Maybe it’s time I got out my poison pen and added my two cents to the scientific record.
Whenever anyone asks me for my favorite scientist, her name comes first.
At a time when women were considered intellectually inferior to men, Noether (pronounced NUR-ter) won the admiration of her male colleagues. She resolved a nagging puzzle in Albert Einstein’s newfound theory of gravity, the general theory of relativity. And in the process, she proved a revolutionary mathematical theorem that changed the way physicists study the universe.
It’s been a century since the July 23, 1918, unveiling of Noether’s famous theorem. Yet its importance persists today. “That theorem has been a guiding star to 20th and 21st century physics,” says theoretical physicist Frank Wilczek of MIT. […]
Although most people have never heard of Noether, physicists sing her theorem’s praises. The theorem is “pervasive in everything we do,” says theoretical physicist Ruth Gregory of Durham University in England. Gregory, who has lectured on the importance of Noether’s work, studies gravity, a field in which Noether’s legacy looms large.
And as luck would have it, today was the day she was born. So read up on why she’s such a critical figure, and use it as an excuse to remember other important women in science.
I’ve been digging Crash Course’s series on statistics. They managed to pull off two good episodes about Bayesian statistics, plus one about the downsides of p-values, but overall Adriene Hill has stuck close to the frequentist interpretation of statistics. It was inevitable that one of their episodes would get my goat, enough to want to break it down.
And indeed, this episode on t-tests is worth a break.
