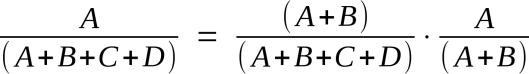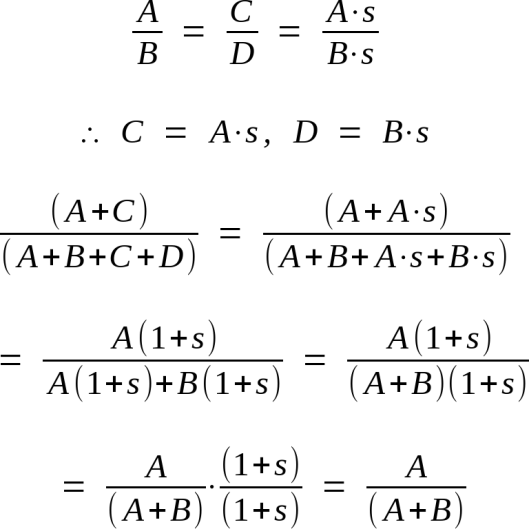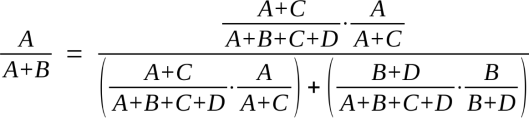[complications arise, as does simplicity]
In the last installment, we calculated the odds of nesting or attempted nesting at site 84744 M.S. to be 92%, based on Hugh’s claim. We also found that daufnie_odie’s claim made us 11% confident in nesting.
Hugh, though, was talking about a different point in time. Our original question only asked if the nesting site had seen a nest or attempted nest, without any other clear bounds. It’s similar to asking “will I ever see heads while flipping this coin;” the more distinct observations we have, the greater the chance of at least one head (or nesting attempt) appearing.
The obvious way to combine these two claims is to consider all the possibilities. If we have two independent events, A and B, then the odds of at least one happening is the sum of the first happening but the second not, the second happening but not the first, and both happening. That isn’t too annoying to add up when we have just two events, but if we use this technique for N events we’ll have to consider 2^N – 1 possibilities. Ouch.
Notice, though, that we’re calculating the probability of every possible observation combination, excluding one: that no events occurred. However, by definition the sum of all probabilities must be one. So if we calculate the odds of that single combination and subtract it from one, we know the sum of the odds for every other combination. We can accomplish 2^N – 1 calculations for the cost of one!
Putting this into practice with our numbers above, we calculate the odds of Hugh being wrong about the nest and the odds of daufnie_odie being wrong, then multiply and subtract that from one, and get 93%. A marginal improvement.
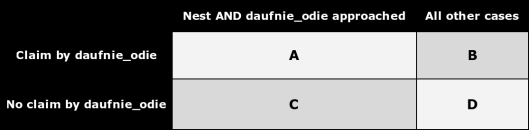
But hold on here; why did I multiply those two together? Let’s pull up a diagram:
 Our goal is to figure out A / (A + B + C + D). We can use a bit of algebra to rewrite that as
Our goal is to figure out A / (A + B + C + D). We can use a bit of algebra to rewrite that as
Oh, there’s our multiplication right there! In English, all we have to do is multiply the odds of daufnie_odie being wrong, by the odds of Hugh being wrong when we assume daufne_odie is wrong.
One problem: we don’t know the odds of the latter, just the odds of Hugh being wrong overall. If those two were dependent events, this could be a big problem, but thankfully they’re independent for our purposes; if we’re calculating the odds of no nest or attempt, we don’t care if two or more people are talking about the same event, we just need them to be wrong about whatever they’re talking about. That means that the vertical partition is exactly as it looks in the diagram, a straight cut across the entire probability space. In math terms, the ratio of A to B is the same as that of C to D, which leads to
So as long as we can be confident daufnie_odie’s claim is independent of Hugh’s, we can treat (A + B) / (A + B + C + D) as A / (A + B) and just multiply.
But when we take a closer look at daufnie_odie’s post, we realize we’re missing some key facts. They spoke up after reading another post by Pollock Myerson, wondering if the person who contacted them was the same as the one who contacted Myerson. Hopping over to Myerson’s post, we learn that he was introduced to someone claiming to have spotted a nest by Caroline Puppy, and that later on a third person contacted Myerson to validate the original tale. Again no names are mentioned, but Myerson, Puppy, and the third person make it clear that they know this nest claimant.
Scrolling back, we see someone named Bryant Tompsin claiming to know a witness to an attempted nest. This doesn’t look like the same person that contacted Puppy. There’s also a comment by someone who goes by “maryann”, who claims to have spotted at least an attempted nest; whether this is the same person that Tompsin, Puppy or daufnie_odie referred to isn’t clear, but it’s probably not Hugh under a different name.
Scrolling forward, we also find a few posts where Pauline Gray claims to have seen a Sexualis Asoltenti attempt to nest, but leaves out what nesting site she saw it at. Puppy reappears, claiming that she was told by someone named Dijai Gruthi that there was an attempted nesting at 84744 M.S., a fact she later confirmed with someone else who witnessed the same nesting. By comparing photos and accounts, it becomes probable that Pauline Gray was talking about 84744 M.S., that she saw it at the same time as Gruthi, and that Puppy’s other person is Gray. In the meanwhile, Tompsin reappears and also claims to have heard of the same attempted nesting from Gruthi.
As all that’s sinking in, we flip open the local birding magazine and find still more. Pauline Gray admits she really was talking about 84744 M.S. and that Gruthi was present for the attempted nest; the unnamed person of Myerson outs themselves as Ali Smyth, a local birder; and a well-respected person named Jim Grandie suggests he saw a nest or attempt at one but waved it off as horseplay, something birds do when drunk. Biff Jag confirms he was around shortly after Smyth’s nesting observation, and someone with the handle “skippingthem” mentions they know someone who was also a witness. daufnie_odie posts again, and confirms that the nesting Ali Smyth saw was not the one they were aware of. Finally, we can infer some information from the state of the nesting site; if it remains constant, that would suggest a nesting or attempt was unlikely, and if it shifted over time then it likely was nested in at some point. Myerson had a look at the long-term state of 84744 M.S., and indeed found evidence of shifting.
Working through all these combinations would be a nightmare. Fortunately, we don’t have to. As we only care if at least one nest or attempted nest happened, we can instead calculate the odds of no nesting occurring and then subtract that from one. This is a much simpler task, which we’ll accomplish in the next installment…
[HJH 2015-07-19: adding some missing links]