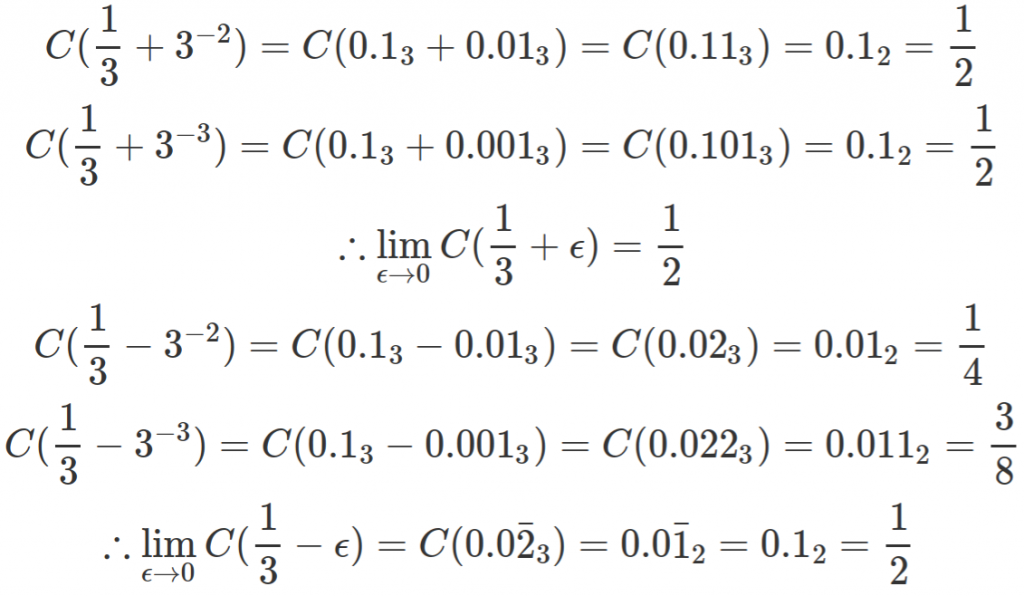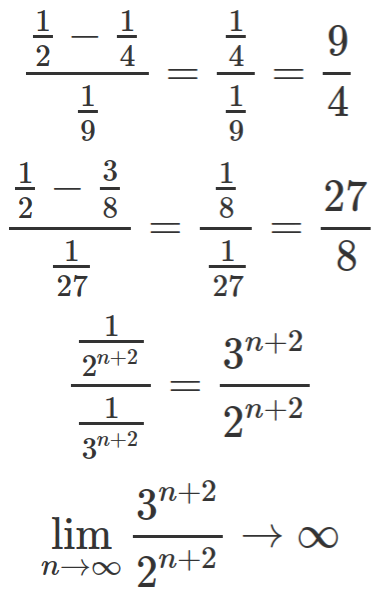You might have wondered why I didn’t pair my frequentist analysis in this post with a Bayesian one. Two reasons: length, and quite honestly I needed some time to chew over hypotheses. The default frequentist ones are entirely inadequate, for starters:
- null: The data follows a Gaussian distribution with a mean of zero.
- alternative: The data follows a Gaussian distribution with a non-zero mean.
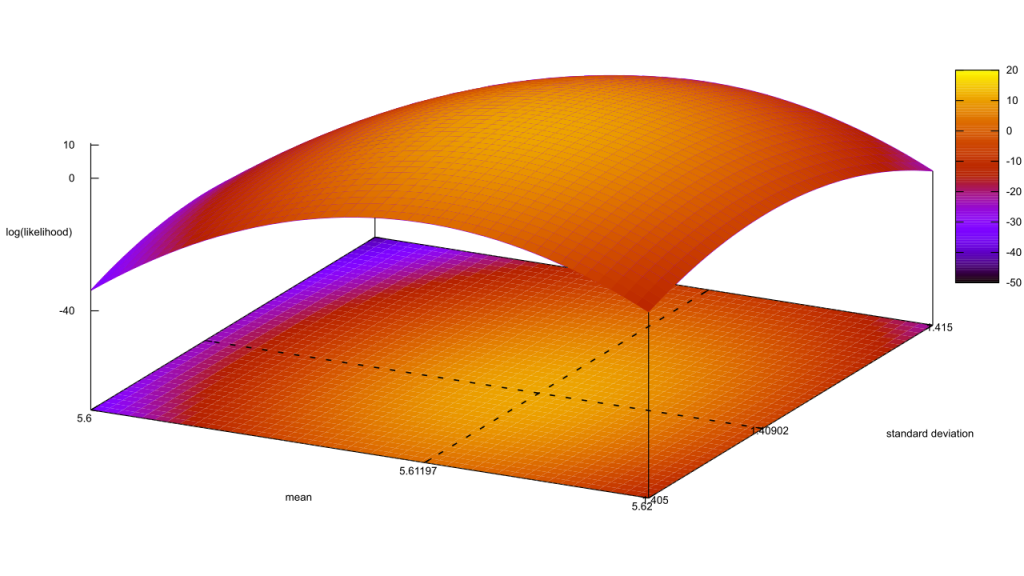
In chart form, their relative likelihoods look like this. [Read more…]


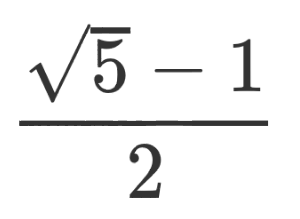
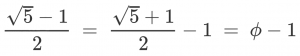
![The Cantor function, in the range [0:1]. It looks like a jagged staircase.](https://freethoughtblogs.com/reprobate/files/2017/05/cantor_function-1024x576.png)