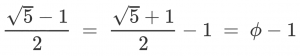If you’ve followed my work for a while, you’ve probably noted my love of low-discrepancy sequences. Any time I want to do a uniform sample, and I’m not sure when I’ll stop, I’ll reach for an additive recurrence: repeatedly sum an irrational number with itself, check if the sum is bigger than one, and if so chop it down. Dirt easy, super-fast, and most of the time it gives great results.
But finding the best irrational numbers to add has been a bit of a juggle. The Wikipedia page recommends primes, but it also claimed this was the best choice of all: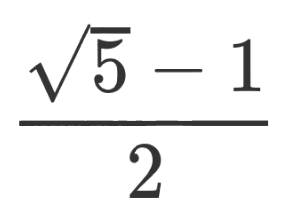
I couldn’t see why. I made a half-hearted attempt at digging through the references, but it got too complicated for me and I was more focused on the results, anyway. So I quickly shelved that and returned to just trusting that they worked.
That is, until this Numberphile video explained them with crystal clarity. Not getting the connection? The worst possible number to use in an additive recurrence is a rational number: it’ll start repeating earlier points and you’ll miss at least half the numbers you could have used. This is precisely like having outward spokes on your flower (no seriously, watch the video), and so you’re also looking for any irrational number that’s poorly approximated by any rational number. And, wouldn’t you know it…
… I’ve relied on the Golden Ratio without realising it.
Want to play around a bit with continued fractions? I whipped up a bit of Go which allows you to translate any number into the integer sequence behind its fraction. Go ahead, muck with the thing and see what patterns pop out.