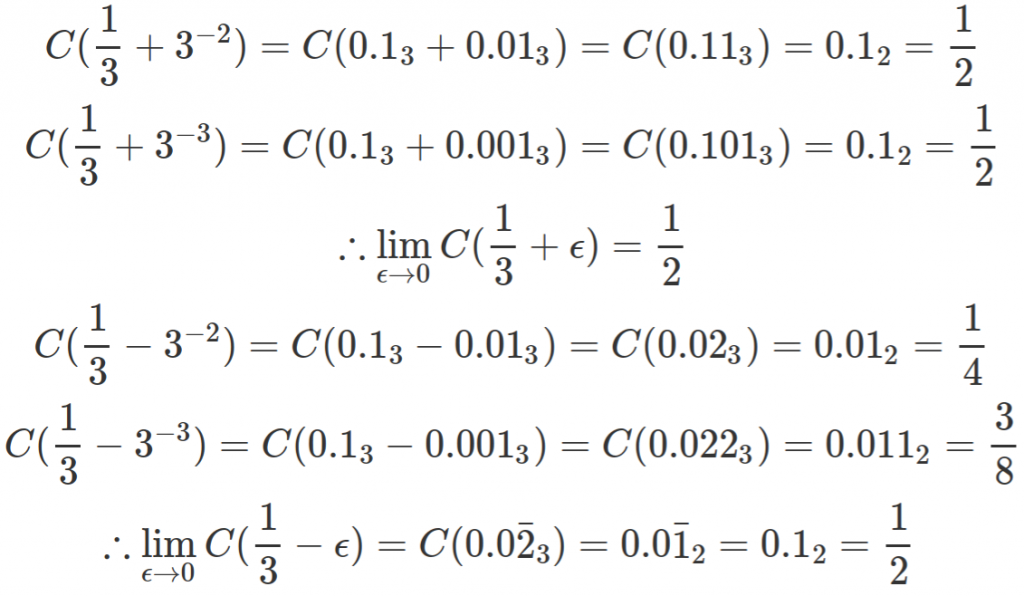Take the Cantor function, a “Devil’s Staircase.”
It looks like a squiggly mess, yet it is continuous and at almost every point there’s a well-defined slope: perfectly horizontal. The only exceptions are at points along the X-axis which are part of the Cantor set, an uncountable number of points with zero length. Even at one of these points, however, the net vertical increase is zero! We can see this by calculating the limits toward a point with a non-zero slope.
Wikipedia has a good write-up on how to evaluate the Cantor function (I used it in the above approximation).
- Express x in base 3.
- If x contains a 1, replace every digit after the first 1 by 0.
- Replace all 2s with 1s.
- Interpret the result as a binary number. The result is c(x).
The point x = 1/3 is part of the Cantor set, and thus satisfies our needs. Following the above rules, the output of the function there is 0.1 in binary, or 0.5 in decimal. Let’s calculate both limits, to get a feel for how much vertical is climbed at that point.
If we approach x = 1/3 from the right, we flatline at y = 1/2 . If we approach it from the left, we wind up evaluating the geometric series y = 1/4 + 1/8 + 1/16 + … to calculate the height, which gets arbitrarily close to y = 1/2 . The height of the “jump” at x = 1/3 vanishes into insignificance! That’s a good thing, as otherwise the Cantor function’s slope would have approached a vertical line and it wouldn’t be a function.
Yet even though every single vertical hop is arbitrarily small, it’s obvious the Cantor function has some sort of vertical increase. How else could it contain both (0,0) and (1,1)? In fact, if you measured the arc length of the Cantor function, it would be two units. Every point where the slope isn’t horizontal it is arbitrarily vertical, so no matter where you put the vertical or horizontal bits you wind up travelling the Manhattan distance between (0,0) and (1,1), which is 2. We know the distance of the horizontal components adds to one unit, since the Cantor set has length 0 and the horizontal distance is 1, so the uncountable number of arbitrarily small vertical “hops” must also have a net length of one unit.
The Cantor function manages to climb vertically without actually climbing vertically. Pretty wild, eh?
Oh, and credit where credit is due, I was introduced to the Cantor function by PBS’s Infinite Series. Check it out for a weekly dose of math.

![The Cantor function, in the range [0:1]. It looks like a jagged staircase.](https://freethoughtblogs.com/reprobate/files/2017/05/cantor_function-1024x576.png)