In an earlier post, I was talking about the economics of entertainment media. As a way of starting that discussion, I introduced a very basic model which I called the Food Truck game. Several food trucks park along a single street, and each customer patronizes the nearest food truck. It’s a neat little problem, similar to the cake-cutting problem, but it’s not a very realistic model of entertainment media.

So I thought about it some more, and came up with some possible adjustments. With these adjustments, I hope to tease out some real implications. The question I want to answer is, what is it like to have fringe tastes in entertainment media, vs having mainstream tastes? How many businesses will cater to your preferences?  What prices will they charge you?

This also plays into a larger discussion I’ve been having, about the differences between capitalist systems, utilitarian systems, and fair systems.  Here I will show that each system leads to a different solution to the food truck game.

Modifying the food truck game

IMHO the main weakness with the food truck game, is that all food trucks were required to charge the same amount. The only way food trucks could differentiate themselves from one another, was by being in different locations.

So let’s introduce variable pricing. Each food truck can differentiate themselves in two ways: location, and price. Now, suppose that each customer is willing to walk 100 meters to save a dollar. Each customer patronizes the food truck with the lowest combined price plus walking distance.

Variable pricing makes the food truck game a lot more complicated, so we’re going to simplify other aspects of the game to keep it tractable. Earlier, I said that the 3-truck problem is difficult, the 4-truck problem is extremely difficult, and the 5-truck problem I wasn’t even able to solve. The more trucks you have, the more exponentially difficult the problem is. But here’s a little physicist’s trick: consider a really large number of food trucks, and just take an approximation. So let’s say that the number of food trucks is very large. If there are N food trucks, they space themselves approximately evenly, and each truck gets 1/Nth of the business. Simple enough.

But perhaps too simple. So I have one more modification, which is intended to address the difference between mainstream and fringe tastes. Let’s suppose that we instead have two towns. One town, representing mainstream tastes, is densely populated, and the other town, representing fringe tastes, is sparsely populated. Let’s say that the two towns are equal in size, but the mainstream town has ten times as many people as the fringe town, in the same amount of space. Trucks are allowed to travel between towns, but the townspeople are not.

So each truck needs to make two decisions: Which town should it go to, and what price should they charge for lunch? Trucks make this decision on the basis of profit-maximization.

Before I tell you the solution, I invite the readers to take guesses: What’s the ratio between the number of food trucks in the two towns? What’s the ratio between the prices in the two towns?

Solution and discussion

The first thing we need to figure out, is the pricing. If there are a bunch of food trucks evenly spaced, then the equilibrium price will be equal to the distance between trucks. That is, if the trucks are spaced 100 meters apart, then the equilibrium price is $1 (the amount that people are willing to pay to save walking 100 meters). I’m not going to go through any of the math (a basic application of calculus), but it’s a simple trade-off. If the trucks charge less, then they get more business, but have smaller profit margins; if they charge more, then they have higher profit margins, but lose business to neighboring trucks.

Note, for the sake of simplicity, I’m ignoring the cost of producing the food. To a first approximation, the marginal cost of production would just be added to the price tag.

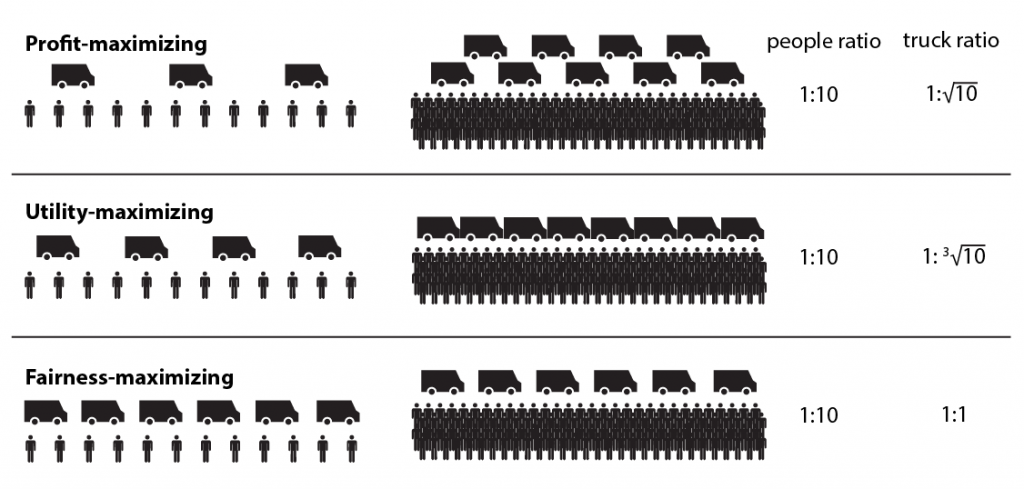
We can see from the start that the trucks will not all crowd in one town, because if they did then a lone truck could capture all the business in the other town. We expect that the trucks will distribute themselves between the two towns, in such a way that trucks in each town will make an equal amount of profit.  With this condition, we can conclude that the ratio of the number of trucks in the mainstream town to the number of trucks in the fringe town, is sqrt(10). The food trucks in the fringe town will be more expensive, again by a factor of sqrt(10). Did you guess right?

In my previous post about the food truck game, I discussed a “centrally planned food truck economy”, which distributes food trucks in order to minimize average walking distance (i.e. maximize total utility). In this case, the ratio of number of food trucks, will be the cube root of 10, instead of the square root of 10. That’s slightly more food trucks for the fringe town. However, the townspeople of the fringe town will still have to walk further than people in the mainstream town.

Finally, we can consider a fairness-maximizing economy, where we want people in each town to all walk about the same distance.  In this case, each town has an equal number of food trucks.

The big takeaway: A profit-maximizing economy is different from an utility-maximizing economy, which is different from a fairness-maximizing economy.  In none of these models, is the number of businesses (food trucks) proportional to the number of people in each town.

Somewhere in there, is an argument that just because only 5% of consumers are in a minority group, does not mean that only 5% of media ought to cater to them.

I think this model is more realistic than before, but there are still plenty of things missing. Just to list a few: a nonzero cost of production, the ability to patronize multiple food trucks, multi-dimensional towns,* non-euclidean preferences, economic disparities, waiting lines, different levels of food quality.

But at this point, I have no intention to expand the model. I think I’ve just about reached the limits of what I can do with it. What do you think?

---

*I also solved the extended problem, where instead of having a town with just a single street, we have a d-dimensional town. (Generalizing to an arbitrary number of dimensions is a very condensed matter physics thing to do.) The correct ratio of food trucks is 10^(d/(d+1)), and the correct price ratio is 10^(1/(d+1)). If the food truck economy is centrally planned, then the food truck ratio is 10^(d/(2d+1)). For higher dimensions, the difference between profit-maximizing and utility-maximizing economies is more pronounced.