One thing I’m interested in is the theoretical economics of entertainment media. For instance, we know that people have a wide variety of tastes in movies, but movie producers aren’t necessarily interested in catering to everyone’s tastes, they’re just interested in maximizing profit. You can imagine situations where this would lead most movie producers to cater to the most popular tastes, and to ignore fringe tastes.
Economists would describe this system as a kind of monopolistic competition. The problem is, monopolistic competition is super complicated and dependent on details, and I for one don’t understand it. So in order to better understand monopolistic competition, I want to build a toy model–the very simplest model that vaguely resembles monopolistic competition. The goal is not to build a realistic model, it’s more of a conversation piece.
Disclaimer: I have no education in economics, I’m more of a game theory guy.
Movies, democracies, and food trucks
Monopolistic competition is a system where different firms produce goods that are differentiated from each other. To make the very simplest model, we’re going to imagine that goods are differentiated from each other along only a single axis. For example, suppose that each movie falls along a one-dimensional spectrum from “drama” to “comedy”. And where a movie falls along this spectrum is the only thing that could differentiate it from other movies. Some viewers prefer comedies, and some prefer dramas, and some prefer dramedies.
Well, maybe the movie metaphor is implausible, so let’s invent another metaphor. Suppose each “firm” is a candidate in a democratic election. The only way candidates are differentiated from each other, is where they fall on a left-right spectrum. Each voter also falls somewhere along this left-right spectrum, and each voter votes for the candidate that is politically closest to them. Each candidate chooses their political position in order to maximize votes.
The democracy metaphor also sounds implausible, so let’s try a third metaphor. Suppose we have a small town with a single street. The only way to buy lunch in this town is from a fixed number of food trucks. All food trucks are identical, and basically the only thing that differentiates the food trucks from one another is their location. Each day, the townspeople, who are uniformly distributed along the street, walk to the nearest food truck, and pay a fixed price for lunch.
The food truck metaphor is implausible too, but we have to settle on something, so food trucks it is. There are two perspectives to consider: that of the townspeople, and that of the food truck owners. The townspeople prefer to minimize their walking distance. The food trucks, on the other hand, don’t care how far people have to walk, all they care about is getting as many customers as possible. And we’re positing that the only way food trucks can distinguish themselves from each other, is by parking in different parts of town (i.e. we’re not allowing them to have different prices, different wait times, or different food). The question is, where should the trucks park?
Solving the food truck problem
What does it mean to “solve” the food truck problem? What we’re looking for, is what mathematicians call the “Nash equilibrium.” The Nash equilibrium is a set of food truck locations, where none of the food trucks can turn a profit by driving to a different location. As it turns out, if there are 3 food trucks, then no Nash equilibrium exists. How can that be?
When there are two food trucks, each truck prefers to be in the center of the town, right next to each other. When a third truck enters the game, that truck also wants to be in the center. But now that we have three trucks all right next to each other, the one in the middle is cut off from most of its business. So that truck prefers to move out from the middle. But now there’s another truck in the middle, and that truck is unhappy. Also, the outer trucks are unhappy because they want to squeeze the middle truck even more. The trucks will continue to shuffle around endlessly, and it’s impossible for all three trucks to be simultaneously happy.
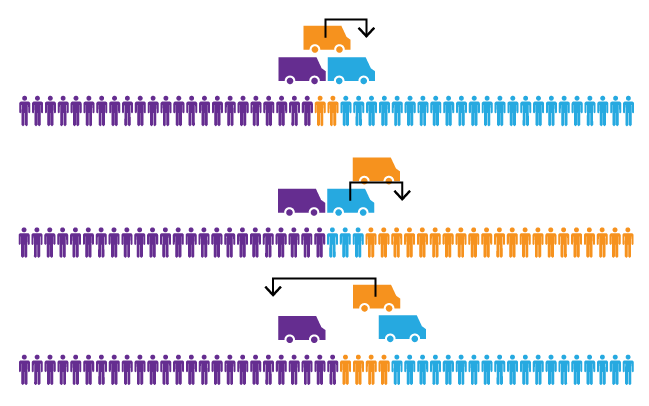
Food truck frustration
So the food truck problem has no solution. Let’s add a few extra rules to ensure that it does have a solution:
- The food trucks take turns choosing their locations. After a food truck chooses its location, it cannot move again.
- No two trucks may park in the same spot, but they may park arbitrarily close to one another.
- If there are multiple equally profitable options, a food truck will prefer the location that most benefits the townspeople (i.e. by minimizing the average walking distance). If there’s still a tie, ties are broken to the left.
With these extra rules, I believe that there is always a Nash equilibrium. In the case of 2 trucks, both trucks will park near the 1/2 mark (the center of town). In the case of 3 trucks, they will park at the 1/4, 3/4, and 1/2 marks. The 4-truck problem is extremely difficult, but I believe the solution is 5/6, 1/6, 1/2, and 1/3. (No I’m not going to prove any of these solutions, that’s too hard.)

Nash equilibria for the food truck game
Discussion
Let me make a few observations about these solutions. The food trucks that cater to the outskirts of town are generally more profitable. At the same time, we can say that on average the people on the outskirts have to walk longer distances.
It would be illustrative to compare to a slightly different situation, what we might call a “centrally planned food truck economy”. Here, the food truck locations are not based on maximizing profits, but on minimizing the average walking distance of the townspeople. In a centrally planned food truck economy, the food trucks will be evenly distributed across the city. If there are 2 trucks, they park at 1/4 and 3/4. If there are 3 trucks, they park at 1/6, 1/2, and 5/6. If there are 4 trucks, they park at 1/8, 3/8, 5/8, and 7/8. In a centrally planned food truck economy, people on the outskirts don’t have to walk quite as far, and all the food trucks perform equally well.
So what implications does this food truck problem have on reality? None, probably. In the real world, people’s preferences are more complicated, people patronize more than one business, there are variable prices, and the optimal strategy is even harder to find.
Questions:
- Which aspects of the food truck problem do you think apply more broadly?
- If you could add just one complication to the food truck problem, what would you add?

Nicely done. Your food truck example is a real model in economics, and I studied it in some detail in grad school. I’m pretty sure your solution for multiple trucks is correct. It’s probably generalizable to n trucks.
Generally speaking, economists will stop at this simple model. Our goal is rarely to calculate the actual optimal spacing of real food trucks. The more important conclusion from this model (and many others like it) is that the competitive equilibrium is not necessarily socially optimal. It’s a dirty little secret that most professional economists know that pure competitive equilibrium is not socially optimal except in special cases.
@Larry,
If you studied this model, did it have a name?
I don’t think the exact solution is generalizable. At first I thought the solution for N>2 trucks was that the trucks would be evenly spaced at 1/(N+1), 2/(N+1), 3/(N+1), etc. I was surprised to find that this was not the case for N=4, and I still don’t know what the N=5 solution is. But still, having evenly spaced trucks is a pretty good approximate solution, and probably more robust to changes in the details of the game.