Scientists at both NASA and the National Oceanic and Atmospheric Administration (NOAA) have announced that 2014 has been determined to be the warmest year since 1880, when instrumental records started being kept. In addition, they say that the “10 warmest years in the instrumental record, with the exception of 1998, have now occurred since 2000”.
Kevin Drum points out that climate change denialists have been artfully using a feature of statistics to deceive their followers to think that there has not been an increase in temperatures. They have used an unusually warm year to try and show that warming is not occurring. How did they do that?
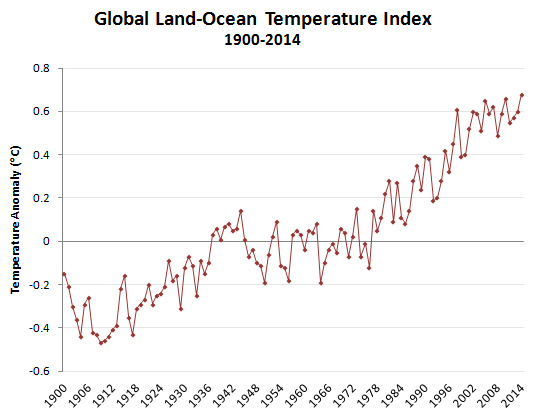
When you plot a graph of any quantity that fluctuates over short time intervals and want to show long-term effects, the choice of starting point is very important. As Drum says, when it comes to the warming of the planet, denialists love to show the year-to-year temperature for the period 1998 to 2012 because it looks like there has been no change at all over that period.
The year 1998 was an outlier, an unusually warm year. If you choose this as your starting point, the next decade will look pretty uneventful. You can do the same thing with lots of other decade-long periods. For example, 1969-85 looks pretty flat, and so does 1981-94. This is typical of noisy data. Planetary warming isn’t a smooth upward curve every year. It spikes up and down, and that allows people to play games with the data over short periods. Add to that the fact that warming really does appear to pause a bit now and again, and it’s easy for charlatans to fool the rubes with misleading charts.
If you shift the two ends by just two years to cover the period 1996-2014, suddenly you see an increase. Of course, what one should do is show the temperatures over a large range for which we have good data of actual global temperature measurements such as for the period 1900 to 2014, and then you see an undoubted increase.

There are some other cute (i.e., disgusting) tricks I’ve seen used. One article had a headline something like, “2014 was Warmest Year Since 1880” (because records only go back to 1880, or whatever year it was). So one guy decided this meant 1880 was hotter than 2014, because he wasn’t about to actually read the article. Another guy said, “What about the other 4.5 billion years?” Because all that global warming that isn’t really happening is due to normal fluctuations, doncha know.
Some day I am going to put my fist through my monitor.
How I sometimes explain this: if you look at my 5K running times from 2011 to now, you’ll see that I’ve gotten slightly faster. So, aging (in my case, going from 52 to 55 years old) doesn’t slow you down, right?
Well, I am running my 5K races approximately 5 minutes SLOWER than I did in 1997-1998; what happened is that I had knee surgery in 2010 and was recovering from that.
The range of years matters!
Here’s an interesting cricket analogy: Global temperatures are batting above their average.
You should drop the outliers before fitting trend lines. A typical procedure is to fit a model, reject any points that are more than two sigmas away from the model, and fit again. The latter fit gives the trend.
You’d fail my classes if you threw away outliers simply because they are outliers. What you say is ok if all you are doing is assessing the influence of those values (although there are numerical measures available to identify their influence) but not for serious work.
“if you threw away outliers simply because they are outliers”
Analysing the reason why a data point is an outlier is important. But if you can’t explain why it is there, it is safer to throw it away. It is probably contaminated by something weird, like a fluke in the equipment with a long-tail distribution. Trying to “unbias” outliers by trying to estimate how much some special case affected them can be even more dangerous.
Try to collect so many data points that you can afford rejecting some of them. Its a form of quality control.
@#6:
Too bad what you describe is not valid statistical practice.
I remember Feynman once suggesting that when you have a set of data, you should exclude the ones at the ends, irrespective of what they are. His reasoning was that experimentalists take as wide a range of data as their instruments and other techniques allow. This means that the ones at the ends are stretching the limits of their abilities and are more likely to be erroneous than the ones that are in the comfort zone of the middle range.
Being a theorist, I don’t know if that practice is followed at all.
It’s not something we’d teach in statistics -- saying it’s ok to remove data values simply because one believes them to be outliers opens the door to all sorts of shenanigans (my findings aren’t significant because of this (these) outlier(s), so I’ll remove them), whether conscious or unconscious.
The problem is in the term “erroneous” -- typically there is no way to determine whether an outlier’s presence is due to some flaw with equipment or simply because it is truly one of the highly unusual measurements that come along. Much of these ideas come from the notion that data can really have a Gaussian distribution in the textbook sense, so if there are outliers there has to be a problem with them. But
-- data is never perfectly normal -- it is simply a textbook idealization of patterns that makes certain calculations simple
-- many sets of data resemble normal distributions in the center region but have longer tails than the normal -- the longer tails essentially mean that data values often considered as outliers are simply large measurements from the population rather than any sign of a problem
Final comment: Feynman’s idea could be described as saying “the influence of outliers should be eliminated completely”. The point of many modern robust methods is to say “the influence of data values on the extremes of the data should be downplayed to some extent”.
I think Feynman’s suggestion might only apply to science data where the limits are due to the limits of the instruments and where you can go no further. I don’t think it would apply where the range of data is not limited in that way.
As for the other suggestion of removing data that are two-sigma off from the trend line, wouldn’t that result in a spurious precision for the line? After all, the scatter of points about a trend line is itself a useful piece of information, no? Edward Tufte provides a vivid example (page 14 in his book The Visual display of Quantitative Information) of several graphs of data points that all have the same mean and standard deviation but when plotted, one of them consists of all but one point lying on a perfect straight line, and the remaining point wildly off the line. If we eliminate that point, then it would look as if all the points lie on a straight line.
It could -- but it is often the case that some outliers are masked by the presence of others, so removing those that are initially visible can reveal the presence of more.
It’s also the case that the “2-sigma” rule can be unreliable precisely because of the presence of unusual values -- both the mean and the standard deviation are as non-robust as things get, so something you might consider an outlier could be within the +/- 2sigma limit: then what? (And again, those are based on the assumption of normality, which is likely not met anyway…)
A quick suggestion for this is: do two analyses, the first with the usual method (usually some least squares based procedure), the second with a good robust method, and compare results -- parameter estimates, confidence bounds, standard errors, etc. If they are in reasonable agreement then any outliers that might be present aren’t exerting seriously degrading influence on your work. If they seriously disagree -- for a regression I sometimes suggest an change in estimated coefficients of over 2 least squares standard errors -- then your outliers are harming you.
But I fear I’m getting too far off track of the message of your original post. Apologies for the near hijack.
I think we mostly agree. The differences come from different goals. Basic vs. applied research. If you are looking for “new physics” you are looking for surprising signals, but if not, you want to ignore them as likely errors.
My background is in engineering, especially signal processing and modeling, and I side with Feynman. The two-sigma limit is a rule of thumb. Practise has shown that in real life situations most things that far from the model can (and probably should) be ignored. You can fine tune the rule: anything within the limit should be included, unless you have a good reason to exclude it; anything outside it should be excluded, unless you have a good reason to include it. But with large data sets you need an automatic rule.
If you don’t like tunable parameters like “two sigmas”, you can run a median filter over the data set before fitting a model. Even that will prevent the denialists from just picking a starting point that fits their agenda.
No, not at all -- that is the whole point. Tossing data because you merely suspect it is bad makes the rest of your analysis suspect.