(Previous posts in this series: Part 1, Part 2, Part 3, Part 4, Part 5, Part 6, Part 7, Part 8, Part 9, Part 10, Part 11, Part 12, Part 13)
The history of analyses of the question “Does a charge falling freely in a gravitational field radiate energy?” is quite fascinating with experts being all over the place, even to this date. The biggest disagreement is over whether the answer to the above question is yes or no. But even among those who agree on the answer, there are disagreements as to the reasons. For example, among those who say that it radiates, some argue that it leads to a loss in kinetic energy and that the Principle of Equivalence may not even hold in the case of a charge falling freely in a uniform gravitational field. Others disagree on what the source of the radiation is.
According to a quick historical review by Rohrlich (references to the works cited can be found in Thomas Fulton and Fritz Rohrlich, Annals of Physics 9, 499-517 (1960)) it was Max Born in 1909 who first derived the electromagnetic fields associated with an accelerating charge. Wolfgang Pauli in 1918 gave a simple argument based on Born’s work that concluded that the accelerating charge does not radiate, a view supported by Max von Laue in 1919 and later by Milner in 1921 and Druckey in 1949. If they were correct, this immediately raised the question of exactly where the well-known radiation formula that one finds in all textbooks breaks down. Conversely, Schott in 1912 also derived the fields due to an accelerating charge and concluded that it does radiate. Various other physicists came down on both sides of the debate and often did not seem to be aware of contrary views. Furthermore, standard texts by C. Moller (1952) and V. Fock (1959) disagree about the equivalence of accelerated observers and gravitational fields while another standard text by J. Synge (1960) even seems to suggest that there is no such thing as the Principle of Equivalence.
Bondi and Gold in 1955 concluded that an accelerating charge does radiate and seemed to be the first to point out the paradox under discussion of a charge falling under a uniform gravitational field, and that any radiated energy would result in a violation of the idea that all particles will fall at the same rate in such a field. They argued that since you cannot physically have an infinite uniform gravitational field, the issue is moot since no experiment can be done to test the outcome. It is true that to create a truly uniform gravitational field, one would need to have an infinitely large, uniform slab of matter, with the two sides being flat and parallel. This is of course, not possible. But thought experiments that might be practically impossible have long been a way to theoretically investigate phenomena, and Einstein in particular exploited them heavily. There is nothing in principle that prevents us from imagining the existence of a uniform gravitational field and seeing where that leads.
It was from the 1960s and onwards that there was a surge in interest in this question. The resolution given by Fulton and Rohrlich, that the falling charge does radiate, was endorsed by David Boulware (Annals of Physics 124, 169-188 (1980), Sidney Coleman (Rand Report RM-2820-RR (1961), unpublished), Rudolf Peierls (Surprises in Theoretical Physics (1979), p. 160-166), and Camila de Almeida and Alberto Saa (American Journal of Physics 74 (2006) 154-158 or at https://arxiv.org/pdf/physics/0506049.pdf) among others.
Richard Feynman (https://www.mathpages.com/home/kmath528/kmath528.htm) was among those who disagreed. Feynman argued that the usual formula giving the power radiated by an accelerating charge as proportional to the square of the acceleration is not generally true but only only applies to cyclic or bounded motions. Luca Fabri (Annales de la Fondation Louis de Broglie, Volume 30 no 1, 2005) also said that there should be no radiation, and so did Nathan Rosen (Annals of Physics 17: 261-275 (1962).
Going in a completely different direction, Noam Soker and Amos Harpaz (General Relativity and Gravitation, Vol. 36, No. 2, February 2004) argue that it is the curved electric field of an accelerating charge that provides the radiation reaction force but arrive at a startling conclusion, that even a charge that is supported at rest in a gravitational field will radiate because such a charge is accelerating in an inertial field.
Due to the acceleration, the electric field of the accelerated charge is curved, and a stress force exists in this curved electric field. The interaction of this stress froce with the accelerated charge is actually the reaction force, which the external force has to overcome, and the work performed in this process is the source of the energy carried by the radiation. The key point in all the considerations is the curvature of the electric field of an accelerated charge. This curvature is created because the electric field which is an independent physical entity, is detached from the charge that induced it, and it is not accelerated with the charge.
How do they arrive at this conclusion? They say that even though the charge is at rest, its electric field gets detached from it and continues to fall.
Prima Facie, the situation of a static charge supported in a gravitational field is considered to be a static configuration. This is certainly not the case. As already stated by Einstein and Infeld and many others, the electric field of the charge is an independent physical entity, which possesses energy(mass) and momentum. It is detached from the charge that induced it, and it is not supported with the charge. It falls in the gravitational field and becomes curved due to this fall.
…Our result that a supported charge radiates, which is based on the curved electric field lines criterion for radiation, is in full accord with the principle of equivalence.
David Rowland (European Journal of Physics 31 (2010) 1037–1051) describes some other disagreements.
Fundamental to a clear exposition of the topic is a conceptual understanding of energy and momentum balance for the problem. However, in this regards recent expositions in the literature still give conflicting accounts. For example, when it comes to uniform rectilinear acceleration, Eriksen and Grøn state that the radiated energy-momentum as predicted by the relativistic generalization of Larmor’s formula comes from the so-called Schott energy-momentum, while Singal has argued that there is no radiation in this case and Heras and O’Connell have argued that radiation is only created during the periods of transition to and from motion with a uniform acceleration and motion with a constant velocity.
As I have said in previous posts, I like Fritz Rohrlich’s approach the best since it seems very careful and comprehensive. He finds that the falling charge does indeed radiate but this does not lead to a loss in kinetic energy and a violation of the principle of equivalence because the radiated energy comes at the expense of the internal energy in the electric field that accompanies the electron. But he acknowledges that there are still major unanswered questions.
The interesting questions at this point are the open questions. If one accepts the equation of motion … as correct, what is the physical meaning of the acceleration energy and the apparently arbitrarily large depletion of the charge’s internal energy by radiation in the course of its motion? If one does not accept this equation of motion, what is the correct equation and the correct radiation reaction of a classical charged particle?
…The extension to general relativity involves the difficult questions of the relationship of metric and electrodynamics. What does radiation mean within this framework? Does a finite curvature of space modify the above problems in an essential way? In particular, could it lead to an exclusion of all motions with dQ/dt ≠ 0 in a natural way? What does energy conservation mean in this frame-work?
Thus, we see that the questions that were answered all seem to have been very simple, but the questions that remain all seem very difficult.
So there we are. I am sure that if I dig deeper into the literature, I would find even more points of view because this is a fascinating question and has attracted quite a bit of attention, especially since the 1960s.
But I am drawing the line here, at least for the present, leaving open the option of revisiting the issue in the future if I come across some really interesting ideas.
In the next and final post in this series, I will give some reflections on this topic.
(To be continued.)

I’m not a physicist, and I’m perhaps being naive, but let’s say the the charge does radiate uniformly in all directions while free-falling in the z direction. Would not the momentum gained by photons expelled with components in the +z direction exactly cancel that of the photons expelled with components in the -z direction, leading to the same net acceleration as a non-charged particle? The energy loss would have to be accounted as a change in mass, I guess, but changing mass does not affect free-fall acceleration.
I am probably being really naive here, but it seems to me that the equations of General Relativity and Electromagnetism within it are well-known, and determinative. So why hasn’t somebody just very carefully solved them for this situation? I’m not asking for a closed-form solution. But if Kip Thorne and folks can tell us what black holes look like from afar, and also find numerical solutions that confirm black hole mergers, surely there is some computer methodology that could be adapted/adopted to just solve the damn equations to sufficiently accuracy to end the debate.
Thanks for the series. Minor typos: “there are disagreement” and “1960s and onwaards” (or perhaps the latter is Dutch? 🙂
[Thanks for pointing those out. I have corrected them. -Mano]
dave57@#1,
Because the charge is accelerating in the downward (z) direction, the radiation is not emitted uniformly in all directions.
Momentum is conserved in a particular direction only if there is no net external force in that direction. What you say would apply in the x and y directions but not in the z-direction since there is a force (gravity) acting along it.
ahcuah @#2,
I am not sure that the issue is one of computation. If it were it should be, as you say, amenable to a brute force computational solution.
The problem may be more fundamental. Although General Relativity and Electromagnetism are both well known classical theories, it has not been possible to create a unified theory of the two, partly because of GR’s non-linearity, that was discussed earlier.
As a result, people have had to make a patchwork theory and there is no unique way to do that, leading to different outcomes.
dave57 @1:
True, but if you admit the possibility of fundamental particles losing mass if they accelerate, you’d have to rewrite particle physics completely. If an electron loses mass by accelerating, we would see electrons of a range of masses, presumably down to zero. But the mass of the electron has been measured to about nine significant figures, and seems to be constant.
ahcuah @2: The problem arises even before you get to general relativity, and is inherent to classical electromagnetism even in a flat spacetime.
As Jackson notes at the end of Classical Electrodynamics, we do em theory largely in two ways; specify the sources (charge, current) and calculate the fields, or specify the fields and calculate motions of particles and currents.
So, we might calculate the motion of a particle in an external field. Then, we might calculate the radiation emitted by the particle, given its motion. What’s left out? The possible reaction of the particle to its own radiation. The reason this has largely worked well enough for us is that the corrections are usually really, really tiny.
And it’s not just a matter of computational difficulty. Many physicists have addressed this, and come up with different answers. And it’s not as though some of them just made mistakes. Interpretation plays a huge role.
What Jackson wrote still holds;
How does it know?
And what happens if you wait to observe whether it radiates or not, then change your mind and either stop it or allow it to continue falling under gravity accordingly?
Mano @5. I’m pretty sure that the non-quantum merger of GR and EM is well-known and well-defined. I agree with what you say if we bring QM into it (but I was only trying to address non-QM). Sorry if I wasn’t clear.
Rob @7. Thanks. EM was not my strongest “field” in grad school.
ahcuah @9:
Well, sort of, but not really. In going from Minkowski space equations to curved space equations, the general rule is to replace derivatives with covariant derivatives. That’s fine if your equations only have one derivative. But while ‘ordinary’ derivatives commute (e.g.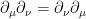 ), covariant derivatives don’t, and changing the order introduces a curvature term. So equations with two derivatives can be ambiguous. In Gravitation (1973, section 16.3), Misner, Thorne and Wheeler admit there is no solution to this other than physical intuition, which they say works in most cases.
), covariant derivatives don’t, and changing the order introduces a curvature term. So equations with two derivatives can be ambiguous. In Gravitation (1973, section 16.3), Misner, Thorne and Wheeler admit there is no solution to this other than physical intuition, which they say works in most cases.
OK, you forced me to grab my copy. I do note that Box 16.1 says that there is mathematical and physical reasoning that resolve the problem unambiguously. Yes, you can argue about how valid that “reasoning” is, but it does look like more than just “intuition” (despite their using that word). For instance, in B(2), choosing the wrong order violates charge conservation. But I’ll concede the point, but ask instead, if one does the calculations I ask for just trying out each possibility, do the results for this particular problem agree with each other? (Again, I guess that’s modulo Jackson, which I am not going to grab my copy of.)
ahcuah @11:
As I pointed out in #7, we can’t even agree on the results in a flat spacetime. So it would seem that em theory isn’t even well-defined there (in the sense that everyone agrees on whether there is radiation in certain situations).
Rob @12: “we can’t even agree on the results in a flat spacetime.”
Well, yeah, that’s why I added “modulo Jackson” in reference to you at #7..