(Previous posts in this series: Part 1, Part 2, Part 3, Part 4, Part 5, Part 6, Part 7, Part 8, Part 9, Part 10)
For convenience, let me summarize the results that were arrived at in the previous post of the calculations of the Poynting vector by Rohrlich for a charge Q and detector D for the following five scenarios. S represents an inertial frame (such as freely falling in a uniform gravitational field) while E is the frame of the Earth.
Scenario 1: Both Q and D are floating freely in empty space in the absence of all forces
Conclusion: D will not detect any radiation and and thus Q is said to not radiate.
Scenario 2: Both Q and D are both falling freely in a uniform gravitational field
Conclusion: D will not detect any radiation and and thus Q is said to not radiate.
Scenario 3: Q is freely falling while D is on the floor in E
Conclusion: D will detect radiation and thus Q is said to radiate.
Scenario 4: Q is on the floor in E while D is freely falling
Conclusion: D will detect radiation and thus Q is said to radiate.
Scenario 5: Both Q and D are at rest on the floor in E
Conclusion: D will not detect radiation and thus Q is said to not radiate.
Let us see how Rohrlich’s results affect the two postulates that began this series of posts:
Postulate #1: If we can eliminate all other forces such as friction, all objects that are dropped from the same height in a gravitational field will fall at the same rate and hit the ground at the same time.
Postulate #2: An accelerating charge falling freely in a gravitational field will radiate energy.
The results of Scenario 3 support Postulate #2, that the falling electric charge will radiate and that radiation will be detected by a detector at rest in the frame.
But there are still three (at least) unresolved issues.
Issue 1: How can it be that a freely falling detector will not detect any radiation from a freely falling charge (Scenario 2) but another detector on the floor of the frame E will detect radiation from that same freely falling charge (Scenario 3)?
Issue 2: This is similar to the first and that is how can it be that a detector that is freely falling will detect radiation from a charge that is at rest on the floor of the frame E (Scenario 4) but another detector that is on the floor of E will not detect radiation from that same charge (Scenario 5)?
Issue 3: This is the basic paradox that started this series of posts. If a detector D on Earth detects radiation from a falling charge (Scenario 3), that implies that the charge loses some energy in the form of radiation and thus one would expect that it will fall more slowly than a neutral particle, thus violating Postulate #1 and the Principle of Equivalence that says that all objects falling freely in a gravitational field will fall at the same rate. If it still falls at the same time as the neutral particle and thus does not violate Postulate #1, that must mean that its kinetic energy is unaffected by the emission of radiation. Does that not violate the law of conservation of energy?
While Rohrlich has done the calculations that led to the results of those five scenarios, some questions arise when we try to get a physical understanding of what is going on.
The first two issues listed above seem to suggest that we (via our surrogate the detector D) can tell which frame we are in (S or E) by noting whether the detector registers radiation or not. This would be in violation the Principle of Equivalence which says that there is no experiment that can distinguish the two cases. This becomes more acute in the photon model where any radiation is thought to consist of the emission of photons. How can a photon be detected in one case and not the other?
One hint to a solution is to observe that the situations where the detector does not detect radiation (Scenarios 2 and 5) correspond to those in which the detector is also accelerating along with the charge. In a 1980 paper that appeared in Annals of Physics 124, 169-188, David G. Boulware says that in such a situation, “all the radiation goes into the region of space time inaccessible to the co-accelerating observer”. In other words, the detector is in a region of space-time that is outside what is accessible to the radiation emitted by the charge. Others have agreed with his calculations.
I have been trying to find a way to explain what this means without bringing in a lot of the mathematics and it has not been easy. Here is the best that I can come up with, though I cannot guarantee that it is wholly faithful to those more careful analyses.
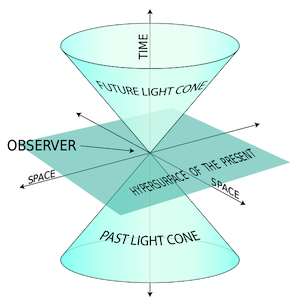 Every single event that occurs in the entire history of the universe (future and past) can be represented by a single point in space-time, since all events must occur in space-time and only one event can occur at any given location at any given time. To help visualize things, we can think of a model two-dimensional space where the horizontal axes represent the two dimensions of space and the vertical axis represents time. A ‘world line’ for any object consists of the line connecting all the points in space-time for that object, each point representing an event that occurred where the object was located. So the lives of each one of us, and indeed any object at all, can be represented by world lines that snake their way through space-time.
Every single event that occurs in the entire history of the universe (future and past) can be represented by a single point in space-time, since all events must occur in space-time and only one event can occur at any given location at any given time. To help visualize things, we can think of a model two-dimensional space where the horizontal axes represent the two dimensions of space and the vertical axis represents time. A ‘world line’ for any object consists of the line connecting all the points in space-time for that object, each point representing an event that occurred where the object was located. So the lives of each one of us, and indeed any object at all, can be represented by world lines that snake their way through space-time.
We have the freedom to choose the origin of the system for any object. If I choose to put myself at the origin of the coordinate system right now (i.e., I choose to put myself at x=y=0 at t=0). then there is a cone-shaped region (called the ‘light cone’) below and above the origin that encompass my past and my future. In 3D space, you have to depend on the mathematics since we cannot visualize four-dimensional space-time.
My world line would begin with my birth at a point in the past light cone and weave its way upwards within the cone (since ‘up’ represents time increasing), the shape of the line depending on how my life unfolded and where I traveled, until it reached the origin, which would be at my desk in my home in Monterey at this moment. My line would then continue upwards into the future. Each object will have a similar world line. An object that never moved would have a world line that went vertically straight up. When two people (or objects) meet, they have the same space and time coordinates at that instant. That means that their world lines intersect at that point, before then going on their separate ways.
The slope of an object’s world line gives the speed with which the object is moving, and that cannot exceed the speed of light. The curved surface defining the cones is due to the world lines of light and the slope of the curve is the speed of light. We see that there are some points in space-time (those that lie outside the future cone) that I can never reach in the future and there are some events in the past (those that lie outside my past cone) that could never have had any influence on me at this instant because in both cases it would require that I (or a signal) travel faster than the speed of light between that point and the origin. The space enclosed by the upward cone and the downward cone encompass all the regions of accessibility for me right now. Note that as time goes by and my world line moves up, there may come a time when I become aware of an event that happened in the past that is inaccessible to me now, because a signal would no longer have to travel at speeds greater than the speed of light to reach me. As an example, we know that light takes about eight minutes to reach us from the Sun. Whatever happens right now on the Sun (even if it blows up) could not have affected me now in any way. But after eight minutes, I will become aware of it.
Thus these cones do not set the boundaries of future knowledge but set the boundaries of cause and effect since any causal connection between the origin to points outside those cones would require me or a signal to travel faster than the speed of light to where I am right now. Such a limit of accessibility to events is called the event horizon.
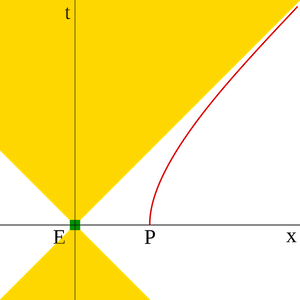 In an even more simplified model of a 1D space, we have just one horizontal axis for space and a vertical axis for time and the cone becomes a V shape but the idea remains the same. When we have an object like the detector D that has a constant acceleration g in its own frame (say by virtue of being propelled by an external constant force such as an engine or falling in a uniform gravitational field), then its acceleration as seen by an observer in an inertial frame S (which is a flat ‘Minkowski’ space), is not a constant but is given by g/γ3 where γ is the familiar Lorentz factor given by 1/√(1-v2/c2), v being the speed of D as measured in S, and c the speed of light. Hence as seen in S, the acceleration of D will start with the value of g when its speed is zero and decrease to zero as its speed approaches the speed of light. This motion of D is described as hyperbolic since the relationship between D’s space coordinate x and time t in S is given by x2-(ct)2=(c2/g)2, which is that of a hyperbola. In the figure, the curved line through P shows the hyperbolic curve of the motion of the accelerated object.
In an even more simplified model of a 1D space, we have just one horizontal axis for space and a vertical axis for time and the cone becomes a V shape but the idea remains the same. When we have an object like the detector D that has a constant acceleration g in its own frame (say by virtue of being propelled by an external constant force such as an engine or falling in a uniform gravitational field), then its acceleration as seen by an observer in an inertial frame S (which is a flat ‘Minkowski’ space), is not a constant but is given by g/γ3 where γ is the familiar Lorentz factor given by 1/√(1-v2/c2), v being the speed of D as measured in S, and c the speed of light. Hence as seen in S, the acceleration of D will start with the value of g when its speed is zero and decrease to zero as its speed approaches the speed of light. This motion of D is described as hyperbolic since the relationship between D’s space coordinate x and time t in S is given by x2-(ct)2=(c2/g)2, which is that of a hyperbola. In the figure, the curved line through P shows the hyperbolic curve of the motion of the accelerated object.
The point is that in this situation, the detector D lies beyond the event horizon of the charge Q and hence will never detect any radiation from Q, preventing D from inferring whether Q radiates or not. Hence the question of whether Q really radiates in Scenario 2 and Scenario 4 but the radiation never reaches D, or whether Q does not radiate, is an experimentally unanswerable one.
That will not be satisfactory to people who believe that we should always have, at least in theory, clear-cut answers to questions. But physics has taught us that there are some formulations of questions that simply cannot be answered, such as whether an electron is really a particle or a wave or what the precise location is of a particle is. We just have to learn to live with that state of affairs and instead formulate questions in terms of things that can be answered experimentally. So, for example, instead of asking how it is that something can be both a particle and a wave, we instead ask what the outcome would be if we do an experiment. It turns out that if the experiment is designed to detect wave-like properties (such as interference patterns), we get that the electron will display a wave-like property. If the experiment is designed to detect particle-like properties (like a particle detector), the electron will display a particle-like property. There seems to be no way to set up an experiment that will display both particle and wave properties simultaneously. To argue that it is absurd that an electron can be both a particle and a wave is to use one’s sense of incredulity to try and impose a view of phenomena that cannot be sustained and leads to seeming paradoxes.
Similarly in this case, to argue that it is absurd that a detector in one state of motion will detect radiation from a charge while a detector in another state of motion will not detect radiation from that same charge is to try to impose one’s personal prejudices on what should happen to an experimental situation. The results are what they are, and we need to come to terms with it. The proper question to ask is what kind of experimental set up will allow us to detect radiation or not.
In the next post in this series, we will look at Issue #3, which raises yet more subtle and tricky questions.
(To be continued.)

I don’t know, it’s kind of like watching a movie.
We see what the camera was focused on. But we know that surrounding the camera, outside of it’s field of view, are a lot of things happening which are both the result of the things we do see and the things we see are also affected by things off-camera. An actor moving to a new position may trigger a stage-light to be moved or turned on, which we may see in the frame. Or a sound cue from off-set may trigger the actors to do something. What appears in the frame of the movie is only a fraction of what is happening on set, and there are certainly things which happen on set which never appear on screen.
Sure, this sort of thing happening without human intervention and as a fundamental weirdness of the universe is something we might just need to accept. But to understand the concept that the detector’s frame of reference will impact whether it detects radiation or not isn’t that different than understanding that a movie camera’s field of view will impact whether it shows the boom mike or not. Put another camera which shows the edges of the set and the set crew working, and you would get a very different experience even if both cameras were recording the same set at the same time. All you are saying is that, like camera placement when filming a movie, detector placement (frame of reference) makes a difference in what is detected.
Which, as an analogy, is probably wrong in every sense.
It’s not clear where you’re placing the charge Q here. If it’s stationary at the origin in S, then the accelerated detector can only ‘see’ the charge for times t < 0. But the question is; what does the accelerated detector see from a charge accelerating with it, i.e. following the same hyperbolic world line as seen from the inertial frame.
Although I have to admit, my initial reaction was that this is similar to what was already discussed for E and B fields, only that the radiation would head into a dimension orthogonal to both of those. The energy following a vector into a previously unknown and possibly undetectable field, call it the R field.
But that is not exactly what Boulware appears to be saying. And what Boulware is weird because it suggests that even though we are not detecting radiation from that charged particle it is actually still losing energy. If we can see detect the charged particle, but cannot radiation which would reduce the energy of particle, doesn’t that mean we should see the particle lose energy or it has to gain energy from another source.
Which seems to relate to your Issue #3.
I’m definitely enjoying these articles, even if I’m only understanding a fraction of what is going on.
flex @3:
In Boulware’s scenario, the charge is accelerating relative to an inertial frame; either sitting in an earthbound lab, or in a ship accelerating in space, say. In both cases, any energy it loses through radiation is not translated into loss of kinetic energy, because it is being supported.
Issue #3 is about a freely falling charge as observed by an accelerating observer.
Rob @4:
That’s a very insightful point. So does that give us a clue as to what’s happening in issue #3, that the acceleration of the observer there is gaining kinetic energy, and hence making it relatively appear that the observed charge is losing it, the mechanics of this by the observed radiation?
Mano:
I may make further comments on the event horizon stuff when I’ve examined it by mentally plugging enough numbers in those equations to know what the hell I’m talking about. Right now I still haven’t worked out whether D is meant to be at P in that diagram, or whether it’s all relative to the observer in S and you can’t think of it independently of that. I haven’t properly understood the event horizon yet; the right edge of the hourglass-shaped possibilty seems to be the path of radiation moving away from the charge, but wasn’t the whole point that the charge is at rest in the accelerating frame and hence isn’t radiating as far as the detector is concerned? But it appears you’re saying that we can’t know that because if it is radiating, the radiation can’t reach the detector anyway. But the diagram hasn’t yet helped me understand why that might be, or where the hyperbolic trajectory comes from.
file thirteen @5:
I don’t know.
The hyperbolic trajectory is the path followed by an object undergoing constant acceleration in its own frame of reference, as seen by an observer in an inertial frame (defined by the x and t axes). The detector is on this path. As I noted in #2, I’m not clear on where the charge is supposed to be, either.
So, it starts off at zero velocity at t=0, and its velocity increases (the slope decreases) as time progresses. But it can’t ever quite reach the speed of light, just asymptotically approach it, in the inertial frame.
The event horizon is the line x=ct; the boundary between the yellow and white areas in the upper right quadrant. The path of the accelerated object always satisfies ct < x. That it is an event horizon is simply seen by imagining a signal coming from a point in the yellow area (ct > x), along the positive x-axis. The signal will propagate at the speed of light along a line parallel to the boundary between yellow and white. So it will never cross the boundary, and the accelerating detector will never see it.
I wish I could provide a clearer answer to the question of the detector and the event horizon. The mathematics that underlie the conclusion are quite complicated in the various sources that I’ve looked at, Boulware included.
As I understand it, the charge Q starts off at E with the same acceleration as the detector D at P. Hence Q’s path will also be hyperbolic but lie in the yellow region. The radiation emitted by it as it moves will lie in a future light cone drawn at each point along its path. But those future cones also lie in the yellow region. The detector will never detect the radiation because D is moving in the white region.
As for the energy conservation Issue #3, that will be addressed in the next post in the series.
Mano @7: Yeah, in that scenario the accelerating detector will not only not detect radiation from Q, it will never even see Q for t > 0. But in Boulware’s (and Rohrlich’s) scenario, the accelerating detector does see the charge, and in fact decides that it has a Coulomb field. So the path followed by the charge is very close to the path shown.
I think an important point to keep in mind, and one I’ve repeatedly seen in the literature, is that the electric (E) and magnetic (B) fields of an accelerating charge each have a part which falls off as 1/r², and a part which falls off as 1/r, where r is the distance from the charge. It’s the 1/r piece which corresponds to radiation, and the detector has to be ‘smart enough’ to pick out that piece, or far enough away from the charge that the 1/r part dominates.
At that point, things do get a bit hairy, and difficult to explain without some advanced math.
Note that we’re talking about classical fields here, not photons; that would require a quantum physics treatment.
I understand the yellow region. I even see how it’s an event horizon for emissions from a charge Q originating at E -- no cones from any future point (upwards on the t axis) can ever cross that horizon, regardless of changes to acceleration. I can “see” that.
What I don’t understand is the hyperbolic line at P. It seems a key issue that the acceleration affects the value of x for D as t increases. (What is x anyway? Is it the magnitude of D’s distance from the starting point for Q (ie. before acceleration)?) But I don’t understand why a future D can’t enter the yellow area, instead asymptotically shying away from it.
Or wait… I just tried tipping the graph 90 degrees left. Now the upwards movement of x becomes clearer because I know the acceleration is always increasing. That means if I construct a “white cone” at any accelerated point of x, that cone can’t cross a horizon line, the same way no yellow one could.
I might have it. The yellow zone is the region where emissions can be picked up; the white zone is where they can’t. All detectors in that frame must clearly start (t=0) in the white zone, and time zero means there’s only a single point of radiation at Q. No detector D can detect radiation from charge Q at time zero because it hasn’t reached it yet! And given there must be a discreet horizon line between the two zones, and any extrapolation into a greater value of t or x results in a yellow “upwards” or white “to the right” cone respectively, neither of which can never reach that horizon line then… no accelerated detector can ever detect radiation from an accelerated charge in the same frame.
Geez, I’m hoping I haven’t merely fooled myself that I understand this…
file thirteen @9: The hyperbolic line is just a distance-time plot for the detector. x and t are the distance (along the x-axis) and time as measured by an inertial observer. If this were non-relativistic, the plot for a body, starting at x=P, t=0, with zero velocity and constant acceleration a along the x-axis would be
x = P + at²/2
which would look like the top part of a sideways parabola on the plot. Both position and velocity would increase without bound as t goes to ∞.
But with relativity, there is always an upper bound on the velocity; c. Doing the rather more complicated maths in this case yields (for a body with constant acceleration in its own frame) a plot which is the top part of a sideways hyperbola, with a constant asymptotic slope such that x = ct.
If someone at some random point x₀ and time t₀ shines a flashlight along the positive x-axis, the front of the light wave would follow a path, for t > t₀
x = x₀ + c(t − t₀)
This has the same slope (indicating speed c) as the asymptote for the detector’s motion. So if the light was flashed at a time t₀ such that ct₀ > x₀ (i.e. in the yellow region), that light would never reach the detector. It’s path never crosses the detector’s asymptote.
Of course, if the detector stopped accelerating, its subsequent plot after that time would be a straight line with a steeper slope than the asymptote (indicating speed less than c), and any signals sent in the yellow region would reach it eventually.
Hope that didn’t further confuse things!
Rob, thanks. I realise my thinking was flawed. The difficult part is trying to envisage why the detector remains outside the horizon line when you bring relativity into it, without admitting defeat and settling for “because the maths say so”.
file thirteen @11:
Maybe some people have an intuition for this sort of thing, but I’m not one of them. What convinced me about different inertial observers measuring different lengths and times between the same two events was the maths. Once you say that all inertial observers see light going at the same speed, the maths leads you to things like length contraction and time dilation.
And of course, this situation is more complicated than that; one of the observers is accelerating.
BTW, I don’t see this as “admitting defeat”, because I absolutely love the maths! 😉
Rob @12:
I don’t have a problem with the maths per se. It’s more that the equations are often presented as a fait accompli when the meat is the discussion, not the conclusion.
Mathematics is a precise shorthand for reasoning, but because it’s not readable at the same pace language is, people tend to skip to the final equation, like presenting the conclusion of the argument without all the thought leading up to it.
The real test of whether you understand something properly is whether you can explain it to someone unfamiliar with it. If someone was to ask “why are atomic bombs so powerful?” and you answered “because E=mc2”, you wouldn’t be wrong, but it would be a cop-out because the listener would be none the wiser. So you explain what the letters mean, and they go “so a little mass is converted to a lot of energy. That makes more sense, and I can intuitively see how you would get a big explosion from that, but how does that actually work? What mass turned to energy and why?” That’s the point at which you start throwing equations at them, or merely say that it comes from relativity, which is long and complicated. Either way will leave them unsatisfied.
My own conviction about length contraction and time dilation didn’t come through mathematics, it was from the thought examples that people had used to explain it to the layperson: the mirror clock on the passing spaceship and so forth.
Now I was following Mano’s reasoning up until it became largely mathematical. I mean, as soon as he added the qualifier (which is a flat ‘Minkowski’ space) I knew I was in trouble, but having the information superhighway at my fingertips meant that I could determine what he meant alone, without having to thrash it out in the comments section. But when he says where γ is the familiar Lorentz factor given by 1/√(1-v2/c2), I’m rolling my eyes and thinking “it’s not bloody familiar to me, matey!”
So it becomes clear I don’t have the background for this. I would like to participate in the discussion. My reasoning ability is as good as anyone’s (it’s certainly a hell of a lot better than my memory). But I don’t speak mathematical or any other type of shorthand, and I think Mano’s blog would be less popular if it was written in shorthand too. If I need a physics degree to contribute positively to the discussion, that’s the point at which I personally might have to “admit defeat”.
Sorry for being so late in replying; real life sometimes gets in the way.
file thirteen @13:
You already have contributed to the discussion (the suggestion to drop the distinction between observer and detector).
When I’m reading stuff which is interesting but largely over my head, I just plough on and hope something sticks, and stimulates further thought. It sometimes works, even if it’s long after I’ve finished reading.
BTW, ‘flat Minkowski space’ just means special relativity, i.e. no spacetime curvature. And the Lorentz factor is just the thingy which you multiply or divide time intervals and length intervals by, to get the time dilation or length contraction.
file thirteen @#13,
I second Rob’s comment. I try to put enough stuff in so that people who have some background get more out of the posts but not too much that others feel completely snowed.
What Rob does is what I also do when I encounter difficult material. I don’t feel that I must understand it all at once but just keep going and later more understanding often sinks in.
I used to tell my students to not come to a halt just because they do not understand something in a textbook but keep going. Learning is not a linear process where you have to know all the earlier stuff before you can learn the later stuff. Often later material helps you understand earlier material.
My intuition tells me that 0.999999… has to be less than 1, but math tells me it actually is 1.
So I have to go with the math, weird though the result seems to me.
(My intuition also tells me planes can’t fly, but that’s another story)
John @16:
Funny story; a common argument about why planes can fly doesn’t really explain how they can fly upside down.
John @16:
(Off topic: this is a surprisingly positive contribution from you John. I had actually expected you to comment, but merely to explain how the statement “My reasoning ability is as good as anyone’s” is logically flawed. I do prefer it when you resist pedantically spelling out the obvious!)
When I was in primary school (US: elementary school) I imagined throwing a rock at a tree. The rock would travel halfway (my reasoning went), then halfway of what remained, and halfway again, and so on forever and never reach the tree (except it did of course). I mention this not as a new thought, but because this is kind of the reverse of what you mention. My intuition said the rock would hit the tree; my limited mathematical knowledge said it wouldn’t, not that I knew it was limited at the time. My point is that “to go with the math(s)” you have to be sure that the maths you’re using are correct, and watertight, and sometimes ascertaining that can be a mammoth task.
(Later I refined my thinking. I had a bouncy ball: a small rubber ball you can buy from vending machines. I imagined what would happen if I dropped the ball and it took a second to bounce to half as high, then half as long to bounce half as high again, and so forth. But as the bounces got smaller and smaller, they would happen faster and faster. My revelation was that once I reached two seconds, my ball would have completed an infinite number of bounces in a finite time! I had discovered limits, but didn’t know what they were. But I also didn’t know that when the bounces got down to around the Planck length, everything would disintegrate into quantum weirdness anyway…)