(Previous posts in this series: Part 1, Part 2, Part 3, Part 4, Part 5, Part 6, Part 7, Part 8, Part 9, Part 10, Part 11, Part 12)
We seem to have arrived at a resolution to the paradox that this series started with that maintains our traditional expectations. Recall that it seemed like two postulates that were thought to be incontrovertible were incompatible when applied to a situation in which an electric charge and a neutral particle were dropped from the same height. It seemed like one or both had to be wrong. Those two postulates were:
Postulate #1: If we eliminate all other forces such as friction, all objects that are dropped from the same height in a gravitational field will fall at the same rate and hit the ground at the same time.
Postulate #2: An accelerating charge will radiate energy.
In the previous post, we arrived at a resolution in which the falling charge will radiate, in agreement with Postulate #2, but that this radiated energy does not result in a loss in the kinetic energy of the charge and thus it will fall at the same rate as the neutral particle, in agreement with Postulate #1.
The way this resolution was arrived at may not satisfy everyone. It involved invoking an aspect of the mass of a charged particle that we may not be familiar with. We looked at some aspects of the subtlety of mass back in Part 5. But there’s more, and this was the introduction of a mysterious source Q that provided the energy radiated by an electron that was accelerating under the influence of a uniform gravitational force. Recall that the rate of energy radiated by the charge was given by the familiar Larmor expression ℛ = 2e2g2/3c3 for a charge e having an acceleration g. Q = 2e2ao/3c2 where ao is the zeroth component of the covariant four-acceleration of the charge given by aμ = dvμ/d𝜏, such that ao = γv.a.
We tend to think of the electron nowadays as a very simple entity, a point-like charged particle that has a definite mass, electric charge, and spin. But that image is deceptive and understanding the electron has puzzled some of the best minds in physics. In the early days, physicists like Lorentz created a model of the electron as a cloud of charge with a non-zero radius. But that raised an unexplained issue of what held the cloud together, since the electrostatic repulsion of a positively charged cloud would cause it to fly apart.
There was a shift to treating the electron as a point charge but this raised other problems. Since the electron has charge, it creates a Coulomb field that surrounds it. This field has an energy density of its own and the ‘mass’ of the electron should include this energy. The problem is that for a point-like particle, the total field energy is infinite, since the Coulomb field and its corresponding energy density become infinite at zero distance.
Another way out is to give the electron a core of small but unknown size so that the field energy integral does not blow up. We can then say that the measured mass of the electron is made up of a ‘bare’ mass and a finite internal energy contribution to the mass due to the field energy (sometimes called the electromagnetic mass), without specifying the size of each. We have some familiarity with this separation of mass components from quantum electrodynamics where the quantum field associated with the electron leads to vacuum polarization and the Lamb shift. (The method of separation of mass components presented here is related to but different in detail from the renormalization process used in quantum field theory that is designed to take care of the infinities that occur there.)
Q is interpreted as part of the internal energy of the electron. It is sometimes referred to as the acceleration energy since its value increases or decreases with the electron’s velocity. (It is also sometimes called the Schott energy.) It is from this source that the energy that is radiated by a charge that is falling in a gravitational field is obtained. Why don’t we hear about this Q more often? What about electrons in a cyclotron that go round and round, constantly radiating since circular motion requires them to have a centripetal acceleration? In that situation, what is the role of Q and how does the energy balancing work out in detail?
Fulton and Rohlich (Annals of Physics: 9, 499-517, 1960) explain that in most situations, Q averages out to be a constant and hence dQ/dt = 0, thus not changing the electron’s mass.
When the motion is periodic or bounded and one averages over sufficiently large times, the term dQ/dt vanishes. Thus, under these conditions, Q represents a fluctuating term and over long time intervals all the work of the radiation reaction goes into radiation. The same is true if one considers the energy balance between an initial and a final state of motion which are equal. It is from these cases that the idea: “no radiation reaction means no radiation” arose. Most problems of interest are of this type, like classical charged harmonic oscillators or betatron orbits. Hyperbolic motion is not of this type. In general, however, there is always an instantaneous acceleration energy as a consequence of the equations of motion.
In those cases, the charge’s kinetic energy does get reduced by the radiated energy and to maintain its speed, energy must be pumped in by an external source.
The case of hyperbolic motion that we are dealing with is an exception. So what is happening to the electron as it accelerates in a gravitational field and undergoes hyperbolic motion? Fulton and Rohrlich continue:
This result seems to lead to a very unphysical picture: The accelerated electron decreases its “internal energy,” transforming it into radiation. Does this mean that the rest mass of the electron decreases? An observer for whom the electron is momentarily at rest (v = 0) will also find ao = γv.a = 0 and therefore Q = 0. Thus we obtain the comforting result that the change in internal energy of the particle does not affect its rest mass. Rather, the radiation energy is compensated by a decrease of that part of the field surrounding the charge, which does not escape to infinity (in the form of radiation) and which does not contribute to the (electromagnetic) mass of the particle.
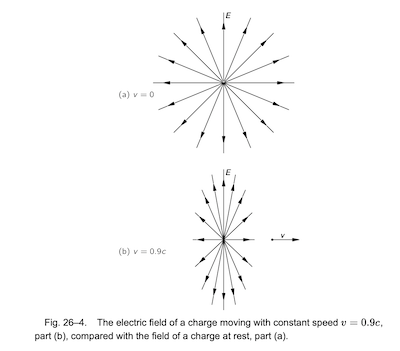 David Rowland (European Journal of Physics 31 (2010) 1037-1051) argues that we should not think of the electron and its accompanying field as a single rigid entity because the radiation reaction force due to the electric field surrounding the change is not able to change instantaneously as the charge accelerates. We know that a static charge has a spherically symmetric Coulomb field surrounding it. If the charge moves with some velocity, that field gets flattened so that the field gets reduced along the line of motion and increased in the plane perpendicular to it, like a pancake, as shown in this figure from the Feynman Lectures in Physics (section 26-1). The greater the velocity, the flatter the pancake gets. But with an accelerating charge, the change in the field distribution does not occur instantaneously along with the change in velocity but there is a lag. This is a consequence of the theory of relativity that says that any cause in one location cannot have an effect in another location within a time less than the time taken for light to travel between the two locations.
David Rowland (European Journal of Physics 31 (2010) 1037-1051) argues that we should not think of the electron and its accompanying field as a single rigid entity because the radiation reaction force due to the electric field surrounding the change is not able to change instantaneously as the charge accelerates. We know that a static charge has a spherically symmetric Coulomb field surrounding it. If the charge moves with some velocity, that field gets flattened so that the field gets reduced along the line of motion and increased in the plane perpendicular to it, like a pancake, as shown in this figure from the Feynman Lectures in Physics (section 26-1). The greater the velocity, the flatter the pancake gets. But with an accelerating charge, the change in the field distribution does not occur instantaneously along with the change in velocity but there is a lag. This is a consequence of the theory of relativity that says that any cause in one location cannot have an effect in another location within a time less than the time taken for light to travel between the two locations.
As Rowland says in his abstract, this difference due to the time lag is the source of the Schott energy.
[T]he precise physical meaning of the somewhat mysterious ‘Schott energy’ … is shown to be simply the difference between the energy in the bound electromagnetic fields of the accelerating charge and the amount of energy in the bound fields of a uniformly moving charge which has the same instantaneous velocity. This difference arises because the bound fields of a charge cannot respond ‘rigidly’ when the state of motion of a charge is changed by an external force.
We see that the mass of an electron is not a simple thing. We should realize that the ‘mass’ of an object is a parameter that we assign to an object in order to arrive at certain results. As long as a consistent use of a single parameter gives us consistent results elsewhere, we are justified is assuming that the parameter refers to an intrinsic property of the object. There is, however, a danger in assigning it meanings that it may not have. We may require that we sometimes give up our idea of the mass of an elementary particle like the electron being a single fixed quantity with no substructure and instead view it as having component parts whose values can shift under various conditions while keeping the total value fixed. Our theories may also require that in certain situations, the total mass may also change for short time periods, such changes being outside the scope of direct detection, so that when we measure the mass, it always comes out the same value. Our knowledge of this would be inferential, based on results than can be measured as a consequence of such behavior. As I said before, intuition can lead us astray in situations outside our experience. In those situations, we have to go where theory leads us.
This result was arrived at using an equation of motion for the falling charge and seeing where it led. Rohrlich and Fulton state that as a result of us not having a unified theory of gravity and electromagnetism, we have to choose an equation of motion as best as we can and accept the consequences of that choice. If one uses a different equation of motion from the one they chose, one might well end up with different outcomes. One has to work out the corresponding consequences and then decide which ones are the most plausible.
(To be continued.)

Dirac considered the point electron surrounded by an imaginary sphere of radius ε. Between two times, this defines a ‘tube’ with a 3D surface surrounding the world line of the electron. He then applies conservation of energy to argue that the flow of energy-momentum through the sides of the tube (call this A) must be equal to the difference in energy-momentum at the two ends of the tube (call this B(t2) − B(t1)).
A depends only on the fields at distance ε from the charge, and is calculable. B depends on what’s going on inside the sphere, and is not calculable. But Dirac assumed the simplest possible form for B; B = kv, where v is the electron’s four-velocity, and k is a constant.
The upshot is that Dirac derives an equation of motion for the electron;
(e²/2ε − k)a = F + I
where e is the electron charge, a is the four-acceleration, F is the four-force*, and I is the radiation reaction force, as discussed in the last post. The first term in the brackets on the left side is the contribution from the fields on the surface of the sphere of radius ε surrounding the electron.
Note that if we choose k = e²/2ε − m, we recover the usual equation of motion (apart from the I term).
You can think of the stuff in the brackets as a large positive contribution to the mass from the em fields (going to ∞ as ε goes to zero), and a large negative contribution (k) from the immediate vicinity of the electron, resulting in a finite sum.
*For Dirac’s calculation, this is the Lorentz force due to an external em field, but it’s generalizable to any external force.
If I read that right, it means that the “squishing” of the electric field as it undergoes acceleration generates the radiation (the diagram helps). Fine. But what happens when the acceleration stops and the field returns to its original shape? Do we have radiation flowing back into the electron to compensate for this “unsquishing” of the field? (That statement seems ludicrous, but by phrasing it that way I’m hoping it will be easier to correct)
Rob @1:
k is not a constant then is it? It has to be at least proportional to e² and inversely proportional to ε. For k to be a constant, shouldn’t those terms be taken out of k to make the equation (1/2 − k)(e²/ε)a = F + I instead? (I realise this may be a trivially obvious change if correct, but I need to be sure I haven’t missed something)
file thirteen @2: ε is arbitrary*, but it’s kept constant for the calculation. In other words, you don’t consider variations in ε while you’re calculating. The charge e is considered constant (about -1e-19 coulombs). So yeah, if you choose a different ε you get a different k. But for a given value, the only things which can vary are the position of the electron (and derived quantities like velocity, acceleration, etc) and the fields.
*Well, it’s assumed to be much smaller than any length we might encounter in a real-life problem, but otherwise arbitrary.
Whoops, charge of electron is about -1.6e-19 C.
file thirteen @2:
It’s not the squishing (or desquishing) of the lines which generates radiation.
Suppose an electron accelerates from rest for a certain time, then stops accelerating. This diagram show what happens to the field lines during acceleration (between the two concentric spheres); they have a component which is transverse (i.e. not pointing straight outwards), and the concentric spheres expand at the speed of light, so this corresponds to outgoing radiation. When acceleration stops, you just have field lines as in the lower diagram above. So there is only outgoing radiation emitted during the period of acceleration.
Rob @3:
Thanks -- I was talking bollocks anyway because I completely left out m
Rob @5:
Ah, thanks, I’d seen the diagram you linked to before, but it was that comment that really switched on the light bulb!
Further to my last comment, the concept of a “deformation” of field lines radiating outwards at the speed of light is very compelling. I had never really thought about how a point source of light (like a star at a massive distance away) can radiate its light in absolutely all directions. It’s not like a scattering of particles, where the particles diverge leaving gaps between them, or there would be some places where you couldn’t see the star. Obvious when you know it, but new to me.