As ever, Online Sudoku Workshop is brought to you by your friendly, neighborhood Crip Dyke.
As billions of eidetic readers will no doubt remember, we last left our sudoku in this position:
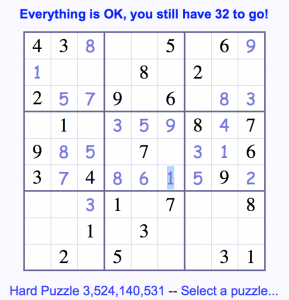
Our genders were, as yet, unaffected by this configuration.
Let’s see what we can accomplish in the Sudoku so that we can move on to the application of the sudoku metaphor to gender. As before, if you’re only in it for the gender, you’re coming into this series a bit early.
We filled in Row F by adding a 1, 6 & 8 after we determined that there must be a 1 outside of the middle square, but clearly in column E by looking at the top-middle square and finding a 1 must exist in either the top-middle box of that square or the bottom-middle box of that square. Since both are middle boxes of that top-middle square, both occupy column E, ruling out a 1 in the intersection of Row F and Column E (which we would call box F:E). With F:D already ruled out and F:A-C and F:G-I already full (of digits other than 1), we could only place Row F’s 1 in F:F.
But what next? In the middle-right square, take a look at the top row. If we fill in those 2 boxes, we’ll have all of Row D complete. The digits missing from the middle-right square, and from row D should be the same, and indeed they are: 2 and 6 are missing from each.
With much left to do, let’s take another look into the future:
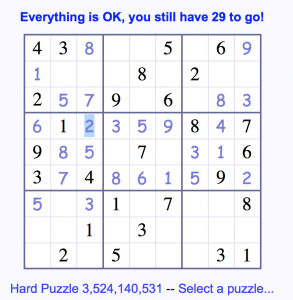
Column A has a 2 in C:A and Column B has a 2 at the very bottom, in I:B (and D:B was full anyway). So neither D:A nor D:B can contain a 2. Place the 2 in D:C as highlighted, and the 6 must reside in D:A.

Doing a quick check on 2s to see if we’re through with them throughout the puzzle makes us aware that while no, we’re not done with 2s, we can place a 2 in the bottom-right square, in box G:H.

That, of course, allows us to place a 2 in the top-middle box at A:E. We’re thrilled with this, because previously we had a 1 in the top-middle box semi-localized to either A:E or to C:E, but we weren’t sure which. With A:E taken up by the properly placed 2 that was pinned down by the 2 in box G:H, we can now confidently and correctly place a 1 in C:E. That top-middle is looking good, Billy Ray!
Even better, there is only one more box left in row C – place a 4 in box C:G (the bottom-left box of the top-right square). That top-middle is feeling good, Louis!
But wait! you say. Who are Billy Ray and Louis? How did a 2 in the bottom-right square pin down a 2 in the top-middle?
Good question. There are 2 ways to go about this. The first is to focus squares. The second is to focus on columns. Neither is particularly easier than the other, but the difficulties involved are different. For the first method, the difficulty is determining how much is known about one square by comparing it to more than one square at a time: in other words, we have to juggle multiple bits of data at a time. in the other, we consider fewer bits of data at a time, but we have to accurately jump to the consideration of the right and relevant bits of data.
Square Focus: In the middle square, any 2 can only be placed in either E:D or E:F. With a 2 in row G (box G:H) and row I (box I:B) we know any 2 in the bottom middle square is in row H. H:E is occupied with a 3 from our givens. So now we have a 2 in either H:D or H:F. I won’t spell it out for you, because I trust you all, but in the top middle box we can now only place a 2 in column E. B:E is full. There is a 2 in row B as well. There is also a 2 in row C. So A:E it is: place the 2 there.
Column Focus: There are 4 boxes left unfilled in column E. We have to place a 1, 2, 4 & 9 in those four boxes. There is a 9 in the top middle box, which means the 9 can’t go in A:E or C:E, but we don’t have any information that would pin it down to G:E or I:E. The 4 can’t be placed in A:E, but could be placed in any of the other free boxes in column E. No help there. The 1, we previously semi-localized, but couldn’t pin down further. The 2, however, can’t be in either of the two free boxes of Column E that are in the lower middle box, because neither row G nor row I can contain a 2. With only 2 boxes left, once we eliminate row C (because of the 2 in box C:A), the 2 must occupy box A:E. The 1 in C:E and the 4 in C:G follow as before.
I prefer the first method. Why? Because I feel it is easier to make progress that way. Why? Because I have an easier time remembering information this way and I don’t want the information to get lost. Whatever method suits your memory, however, works fine.

Instead of starting with a number and pinning down a box, let’s start with a box and pin down a number. See that highlighted 4 in box B:D? Previously we had 7 boxes filled in the top-middle square. That box could only have contained a 3 or a 4. Cross off the 3 (by elimination of other 3s from column D because of the 3 in box D:D) and you only have 4 as a possibility for that box. Likewise, with 8 other numbers filled in for the top-middle square, the box B:F can now only contain a 3.
Note that we can also say that there are only 2 possible locations for a 3, but B:D is eliminated by the 3 is D:D and thus we place the 3 in B:F, then the 4 in B:D. I mention this to show that in many cases one methodology is interchangeable with another. We may have a bias (for whatever reason) of looking first to digits, then to their location, or first to locations then to determining a digit, but the logic leads us to the same place.
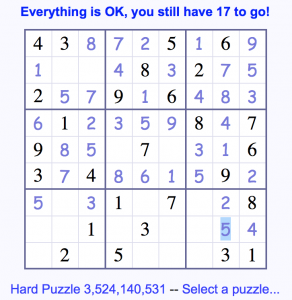
Since there cannot be a 5 in column G other than the already-placed F:G, the bottom-right square cannot have a 5 in G:G, H:G, or I:G. With five boxes filled, the digit 5 must be placed in the center of that square, in box H:H.

The middle square needs a 2 and a 4 placed. One is in box E:D, the other in E:F. The 4 in B:D rules out a 4 in E:D, so we place the 2 in the highlighted box E:D and the 4 in E:F.

The two in the middle square gives us our 2 in the bottom-middle square. The 6 in H:D and the 8 in I:F follow directly from having the 2 occupy H:F, removing the only other possibility for the each of those digits in the bottom-middle square. With the assistance of the 8 in I:F, the bottom-left square now gets an 8 in H:A.

Here we have very little to learn: we rush the left side by placing a 4 in G:B and using that to kickstart the completion of the bottom-left square. That information finishes our top-left square and bottom-middle square.

And, in no time, we have the bottom-right square complete.
Easy-peasy, right? Conga-rats are dancing for your success in solving a hard sudoku puzzle.
Okay, there will be an interlude for one sudoku brain-teaser, then I’ll try to construct a metaphor that will illuminate something or other about gender. Not that I’ve had it in mind from the beginning, of course. No. I’m just [Derald Sue] Winging-it.
Where can I play sudoku?
The screen shots above were taken during my puzzle solving at websudoku.com. I have no idea if they’re the best, worst, or otherwise among sudoku sites, but they were tops in an english language search when I went to go ogle puzzle possibilities and I’ve never seen any reason to try anything different.
In comments on the first Online Sudoku Workshop, many people mentioned the sudokuwiki.org sudoku solver as a great information source and a place to both play sudoku and to learn more about how best to solve these puzzles.


Thanks for the post, Crip Dyke.
After learning the strategy, I tried to jump ahead. I ended up finishing the puzzle successfully, but I had to do some backtracking when my original solution wouldn’t work. My backtracking was going very slowly, so I started from the beginning of the puzzle again. Is there any easy way to backtrack on Sudoku puzzles without having to start from the beginning?
“Doing a quick check on 2s to see if we’re through with them throughout the puzzle makes us aware that while no, we’re not done with 2s, we can place a 2 in the bottom-right square, in box G:H.”
I got lost at this step; why can’t the 2 be in H:H instead, at this stage?
@devnll #2
there has to be a 2 in row G, and G:H is the only space in row G that can be a 2.