I spent my vacation in upstate New York in a cabin on a lake contemplating the big questions. If anyone has been able to follow the past few posts, then this is a continuation. Intelligent designers, who include many physicists, say that the fine-tuning of the universe and its origin would not be possible if we didn’t believe a God did it. Scientists do not know why the constants in the laws of physics are the values they are instead of some other values. But they do know that it cannot be due to physical necessity because we can alter the laws and still create universes. Just not universes that allow for life. It cannot be due to chance, at least not according to half of the physicists, because the probability of us getting our constants and not some others is extremely small.
At least that is the standard narrative given. Of course, I had to determine what was behind this, which is what I do for all posts. I went over all of the nuances of each side’s argument and spent countless hours in email exchanges with experts in cosmology, statistics, and the philosophy of science. I also, albeit reluctantly, embraced Bayes’ theorem, so I could speak their language. And despite my bias toward naturalism, I remained neutral throughout my research. In fact, it was a rollercoaster of a ride where at times I would be convinced by either side. If it were not for recalling how real science is done, I would have advised atheists to keep silent on the topic. To my surprise, my conclusion is that the practice of fine-tuning is not only theologically motivated but metaphysical. I assumed the findings were “scientific”. Although there is nothing wrong with asking questions about what could have been, the assumptions used in calculating fine-tuning are likely obscuring what is actually behind it all.
[This can be used as an accurate reference to understanding how physicists argue fine-tuning. If we want to know why aspects of fine-tuning are not scientific, then we can infer for ourselves here or wait until the next post. I will also be including an argument demonstrating that fine-tuning is compatible with naturalism. This is not a contradiction since life is sensitive to the universe’s parameters. I reject the metaphysical methodology of fine-tuning, but I do not reject that life depends on the universe’s parameters. Furthermore, the public debate is not over whether or not the constants need to be just so in order to permit life as we know it but rather about interpreting what a fine-tuned universe can tell us about the true nature of the universe.]
The Obstacle of Fine-Tuning

Are we really this obnoxious? Atheist Sir Fred Hoyle. [5]
A common sense interpretation of the facts suggests that a superintellect has monkeyed with physics, as well as with chemistry and biology, and that there are no blind forces worth speaking about in nature. [5]
The above is from an atheist physicist who was instrumental to many findings in cosmology. Hoyle was against the idea that the universe may have a beginning to the point that he labeled it as the “big bang”. This was out of mockery since Genesis I predicts that the universe has a beginning. The evidence for fine-tuning may not have been enough to reverse his atheism, but it did make him favor the theory of intelligent design by aliens. The point is that the evidence that the universe is fine-tuned for life is convincing to many and poses an obstacle to naturalism. It is a challenge because according to many physicists, the universe was just as easily likely to have another set of laws with constants as its current set of laws. But any laws but our own would not permit life. Physicists do not know why we have our constants because nothing more fundamental can explain them. They are of course required for the math to work. As the intelligent designers say, it is as if some agent dialed in these constants to permit life.
But what exactly does it mean to fine-tune the universe? This means that the constants within the laws of physics take on values that allow for life on Earth to be possible. They cannot vary by much and still permit life. For example, the cosmological constant is fine-tuned to one part in 10^90 or 1/10^90. If it were any smaller, then the universe would have collapsed within one second upon its creation, or any larger, and the “structure formation would cease after 1 second, resulting in a uniform, rapidly diffusing hydrogen and helium soup” [1]. Examples like this also exist for other life-permitting constants, which include the electromagnetic, weak, and strong forces, two constants for the Higgs field, twelve fundamental particle masses relative to the Higgs field, and more (3).
The calculated entropy implies that out of the many possible ways the available mass and energy of the universe could have been configured at the beginning, only a few configurations would result in a universe like ours. Thus, as Paul Davies observes, “The present arrangement of matter indicates a very special choice of initial conditions.” [In fact, the arrangement had to be so precise that its fine-tuning would be 1 in 10^(10 raised again to 123) [5].
The fine-tuning of the universe that allows life not only requires fine-tuned constants, but it also requires other parameters to be configured just so. Any physical system, including our universe, has parameters, boundaries, and initial conditions. These initial conditions include specific configurations of mass, energy, and entropy. For example, if the matter in the universe was a bit different, then the matter would clump together and cause only black holes to exist, resulting in no stable galaxies or stars. In the beginning stages of the universe, its expansion rate would have been a function of its density, which had a value of 10^24 kilograms per cubic meter. If the density differed by more than 1 kilogram per cubic meter, then galaxies never would have been created [5]. Some have disputed which measurements are to be qualified as fine-tuned and how fine-tuned they are, but no one denies that life is sensitive to its parameters. In other words, if the constants were somewhat different, we would not be here.
We need to define fine-tuning and the fine-tuning argument and clarify what we mean by constants, laws, and universes.
- Fine-tuning: when something, e.g., a parameter with a numerical value (constants in the laws of physics), requires a certain degree of precision to get an effect (life) such that anything outside of this precision or range ceases to get an effect (life)
- Fine-tuning-argument: the proposition that life-permitting universes are rare from the set of possible universes
- Constants: the values, sometimes with units and other times without, that are physically derived through measurement and found within the laws of physics. The constants are measurements of mass-energy and are required for the laws to make accurate predictions about the behavior of energy and matter.
- Laws of Physics: The following dynamical equations are used to describe the universe: Friedmann-Lemaître-Robertson-Walker metric and General Relativity, the Standard Model Lagrangian, and quantum field theory [1].
- Universe: a connected region of spacetime over which physics is effectively constant. [2]
The Philosophy Behind It All
If we assume that the physical constants in our laws of nature are brute facts, then that is the same thing as saying that they took the values that they happen to have for no reason at all from among the set of metaphysically possible values. [6]
Since there is no physical explanation for why the constants take on the values that they do, we are left with our imagination. When we imagine the possibilities of something, then we are doing philosophy. The type of philosophy where we ask what could have been is modal logic. Modal logic includes concepts such as physical, logical, epistemic, and metaphysical possibilities along with possible worlds and brute facts. This gets complicated fairly quickly, so we will keep it simple. Something that is logically possible means that there are no contradictions of terms within sentences. For example, it is logically possible that a unicorn exists although it is not physically possible. It is not, however, logically possible for a married man to be a bachelor. Although metaphysics is about the nature of something, metaphysically possible is what could have been actual. An actual world is the total state of affairs that actually exists, while a possible world is the complete way things could have been. Something is physically possible if it is metaphysically possible given the laws of physics in that universe. Finally, a state of affairs is an arrangement of things [6].
With some degree of confidence, we can calculate what the universe would be like with different fundamental constants. [1]
Most philosophers label fine-tuning as a brute fact or contingent. This means that something is true by virtue of the way things are but also could have been otherwise. Contingent facts must be true in at least one world but not all and do not entail logical necessity. By contrast, metaphysical necessity is something that must be true in all possible worlds and could not have been otherwise. When we use our imagination toward how something could have been different, we create a possible world, which is a complete description of what could have been. When physicists use the laws of physics with different values for the constants, they are creating metaphysically possible worlds. However, the literature is not consistent since philosophers and scientists do not all agree on the definitions. The physicist Paul Davies claims that physicists can only create laws for logically possible universes but not for physically possible ones. We cannot tell which universes are physically possible only that the laws are physically possible.
Recall that the constants are fine-tuned because if they are any different, then the universe is no longer life-permissible. Since we are the product of life-permitting conditions, then it should not be surprising that we observe life-permitting conditions. This is the weak anthropic principle. Philosophers, however, are asking a different kind of question. Why do we have our constants and not some other constants? How do we go about conceptualizing this problem? How do we know, for example, that the universe could have been different? Maybe we do not think physicists are justified in simply changing the constants and labeling our universe a logically possible universe. Perhaps the universe with its constants is a necessary truth and just is. None of this seems to matter because most are motivated to ask questions that require there to be different possibilities. This quickly becomes a challenge.
The Probability Behind It All
There are no actual possibilities besides our own universe since we do not observe how frequently universes in nature end up with certain constants. So physicists use our universe and the logically possible universes that they have created. Now that we have different possibilities we can now ask what could it have been. This requires probability theory. There are multiple ways of interpreting probability, but we look at epistemic versus frequentist-classical. Classical probability uses the principle of indifference to claim that each event is equally likely to occur. So each event has a probability of 1/n, where n is the number of possible outcomes in the probability space. If we take a coin and toss it indefinitely, then we will get a ratio of head to tales that will converge to 50%. This is the law of large numbers, which allows the classical interpretation to be equivalent to the frequency method in the long run. A frequency interpretation is a physical probability that is objective since it captures something about the physical world. This interpretation is what we intuitively understand to be what probability means and is also what most scientists use.
We are concerned with the apparent intractability of obtaining a probability distribution for the various possible universes that might have existed, since in standard probability theory any such distribution cannot simultaneously satisfy three desiderata: that it be defined across the entire logical space of possible universes; that it be Euclidean, assigning equal probabilities to equal intervals for each constant; and that it be normalizable under the constraint of countable additivity. [4]
The philosophy of different possibilities from above addressed the problem of how we imagine universes. Bayesian probability is how we deal with situations where events may have only occurred once and are not physical probabilities. These are epistemic since they are degrees of belief that we hold of how likely something is or is not true. These are thought of as subjective probabilities but only in the sense that they stem from an individual. If physical frequency probability data is available, then this could be used as a source in the calculation. Typically when we use physical probabilities, we want to be sure that they obey the laws of probability theory. This would include being normalizable, where the sum of the probabilities is unity, as well as having the property of countable additivity, which means that we must be able to count and add the probabilities of events that are mutually exclusive. Despite the challenges that the above quote from Timothy & Lydia McGrew poses to the physicists, they claim they can calculate the probability of life-permitting universes from the set of possible universes. They must jump through some hurdles first.
Both of the sets that Barnes and Collins use are finite, so we would end up with either multiple inconsistent probability estimates or an arbitrary partition. [6]
The physicists assume that the constants can take on any real numbered value, creating a new set of laws that constitute a logically possible universe. They choose an equally likely or uniform probability distribution, invoking the principle of indifference since the field of physics offers no information on which values are more or less likely to occur. Since there is an infinite amount of values that the constants could become, this would make it not normalizeable (sum to unity). To get out of this problem, they must truncate the possible values that the constants could take on. This only creates another problem called the partition problem. Choosing any particular partition of the constants, however, would appear arbitrary and would alter the probability assignments in an arbitrary way. They must justify the use of a unit to divide the space. This unit even if justified would still create inconsistent probability assignments. This shortcoming, claims the philosopher Wallace, is applicable to the work of Luke Barnes and Robin Collins [6].
Countable additivity provides a way of modeling important basic principles of rational consistency, and this is not merely desirable but necessary in a well-rounded conception of epistemic probability. [4]
The physicist Luke Barnes’ solution is to use units of Plank since the laws of physics break down after certain values which will create the needed partition. This is not necessarily an arbitrary choice since it is informed by the laws themselves, and Barnes claims that does not follow logical or metaphysical possibility. If it does not follow logical or metaphysical possibility, then we cannot justify how to conceptualize the possible universes. In the end, physicists claim that when they use epistemic probabilities they can replace the countable additivity requirement with the relaxed condition of finite additivity. They justify this by appealing to Cox-Jayne’s, and de Finetti’s theories and the subjective nature of epistemic probability [2]. Although physicists routinely deal with similar problems when working with infinite uniform distributions, which is known as the measurement problem, this may not matter. This is because they make claims using epistemic probability, see quote, which affects whether or not the results will be logical.
The Bayesian Method Behind It All
Bayes’ theorem, and indeed, its repeated application in cases where the probabilities are known with confidence, is beyond mathematical dispute. [3]
We need to talk about Bayes’ theorem in order to speak the language of the physicists and debaters. Bayes’ theorem is a conclusion from a conditional probability axiom. It is a way to update our current knowledge of how likely something is true by taking into account our best estimate of what happens after we observe the evidence. It can be used to not only predict the chances of a physical event occurring given some knowledge but also the likelihood of claims that deal with more complex states (i). In other words, we can use Bayes’ theorem in accordance with propositional logic to get an idea of how likely everyday or even metaphysical claims are. For example, we may state the claim that naturalism is true given that fine-tuning is true. Although there is no consensus on how to interpret probability, we think of these events or states of reality in terms of degrees of uncertainty and not as frequencies. A frequency interpretation of probability is when we observe the long-term behavior of physical events. If we, for example, flip a coin many times, it will average out to a probability of 50%. This is how scientists interpret probability. Despite this difference, Bayesians can still use a frequency source as their uncertainty. When we use Bayes’ theorem, we will be using it to assess the strength of evidence in favor or against a hypothesis, which we call evidential probability. The theorem is shown below.
Equation 1: Baye’s Theorem
P(H|E) = P(H)*P(E|H) / P(E)
It says, starting from P(H|E), that the probability of the hypothesis being true given the evidence is equal to the probability of the hypothesis being true multiplied by the probability that the evidence is true given the hypothesis, which is all divided by the probability of the evidence. These uncertainties or probabilities have names associated with them. P(H) is the prior probability that can be thought of as how typical the hypothesis is, P(E|H) is the likelihood probability or how expected the evidence is given that our hypothesis is true, and P(E) is the marginal likelihood, which is the probability of the evidence. Interestingly, this way of interpreting Bayes corresponds with the argument to the best explanation, or ABE, a form of abductive reasoning. We will be using the specific hypothesis, from equation 2 below, of the probability of naturalism being true given fine-tuning is true. The prior is the probability of naturalism being true, the likelihood is the probability of either observing fine-tuning given naturalism is true or how expected is fine-tuning on naturalism, while the marginal is the probability of fine-tuning being true. Using the law of total probability, P(F) can also be written as shown. Although we can compare our hypotheses to others, see P(F’), we will not have a need for this.
Equation 2: Baye’s Theorem
P(N|F) = P(N)*P(F|N) / P(F)
P(F) = P(N) x P(F|N) + P(~N) x P(F|~N)
P(F’) = P(N) * P(F|N) + P(H2)* P(F |H2) + P(H3)* P(F |H3) + …
P(N|F) > P(N) if and only if P(F|N) > P(F), then evidence is in favor of hypothesis
P(N|F) < P(N) if and only if P(F|N) < P(F), then evidence is against hypothesis
- Posterior probability P(N|F): the probability of the hypothesis of Naturalism being true given Fine-tuning
- Prior probability P(N): How plausible is Naturalism prior to observing the Fine-tuning
- Likelihood probability P(F|N): the uncertainty of observing Fine-tuning given that Naturalism is true
- Marginal probability P(F): the uncertainty of the evidence of Fine-tuning
Equation 3, below, is a statement about probability using Bayesian statistics. Bayesian statistics allows physicists to work with probability distributions. Thus far, we have been assuming that Bayes’ theorem inputs point probabilities; for example, P(B|A) = 0.5, where the probability takes on a single value. The main difference is that these events can take on ranges of different probabilities and are called random variables. A more detailed explanation is provided in the notes. The equation uses the law of total probability since an integral is a summation, and marginalizes over the constant α while treating them as nuisance parameters [1]. Marginalizing removes the α event or parameter, and we are left with the probability that the Data is true given that the physical Theory (laws of physics) and the Background information are true. Throughout the calculations, physicists assume methodological naturalism but not naturalism. The Data D is the same as the fine-tuned universe, F, that permits life and since Naturalim N does not affect anything, then we can plug in N and replace D with F. The result is P(F|TBN) or simply P(F|N), which if we use equation 2, is the value that theists argue is very small. In fact, the physicist Luke Barnes claims by multiplying all the constants’ likelihoods, we end up with a value of 10^-136. Since P(F|N) < P(F), then P(N|F) < P(N), which means that the posterior is less than the prior. When this occurs, then our evidence of fine-tuning does not support naturalism. Theists believe that they have a slam dunk.
Equation 3: Bayesian Statistics
P(D|TB) = ∫p(D|αTB)p(α|TB) dα
- Where α is the value of the constant and the integral is computed over the range R of the constant.
- This gives us the definition of a fine-tuned value which will be a very small value.
Theists’ Conclusion
- It can be shown that P(D|TB) is the same thing as P(F|N), which is the likelihood of fine-tuning given Naturalism.
- Theists take the small value of P(F|N) and insert it into equation 2.
- Since P(F|N) << 1 and < P(F), then P(N|F) < P(N).
- Thus, the evidence of fine-tuning is against the hypothesis of Naturalism.
The Math Behind It All
When calculating fine-tuned values, our background does not give us any info about which possible world is actual. The physicist can explore models of the universe mathematically, without concern for whether they describe reality. [2]
At this stage, we are ready to do the actual calculation of a fine-tuned value. We have learned that modal logic can help us to imagine possible universes and probability theory can help us to create a probabilistic statement. Fine-tuning is the probability of life-permissible universes out of the set of possible universes in such a way that the universes acquire their constants for no particular reason at all. This makes it a brute fact. We claim this is true because physicists have no problem creating logical universes by varying the values of the constants. When they do so, the universes outside of a tight range do not allow for life to exist. We then learned that there are different interpretations of probability. We must use an epistemic interpretation which is Bayesian. Do not get confused because there are two calculations. The first one uses Bayesian statistics to predict the likelihood of fine-tuning (Equations 3, 4), which is literally a fine-tuned value, while the second one (Equation 2) uses Bayes’ theorem to predict that fine-tuning is not compatible with naturalism. Intuitively, we can think of fine-tuned values as a ratio of life-permitting universes to possible universes (vastly more non-life-permitting). Does the denominator contain the constants that non-life-permitting equations have used? Not necessarily. This is a mathematical model that serves the abstract purpose of claiming that “if a universe were chosen at random from the set of universes, what is the probability that it would support intelligent life[1].”
A quantity is fine-tuned in physics when there is no theoretical reason for it to take the value that it has but it must take something close to a very specific value to get the observed outcome. [6]
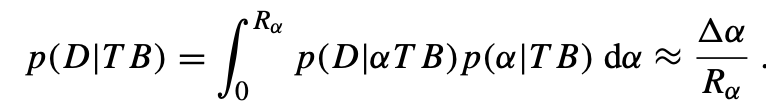
Eq. 4: How to compute a fine-tuned value [2], (vii).
The analysis of the assumptions going into the paradox indicates that there exist multiple ways of dealing consistently with uniform probabilities on infinite sample spaces. Taking a pluralist stance towards the mathematical methods used in cosmology shows there is some room for progress with assigning probabilities in cosmological theories. [7]
Let us try to use the formula above for what the density of the universe was at the time of the Big Bang, which was 10^24 kg/m^3 +/- 1 kg/m^3. R = 10^24 +/- 1 and Δα = (10^24 + 1) – (10^24 – 1) = 2. We get 2/(10^24 + 1). If we change the constant α, but only within the narrow interval of α = +/- 1, then we get life-permissible universes. p(D|IαTB) is equal to one only around Δα and zero elsewhere. p(α|TB) is the prior probability which is the uniform distribution that expresses our indifference to what the parameter of the constants looks like, which is dα/R. What we are doing is calculating the area under the curve, where Δα is the width and 1/R is the height. The literature quotes a value of 1/10^24, which is approximately equal to our calculation. If we think of the denominator as the possible values that are non-life-permissible universe can take, is it true that we have models that create universes within the range of 0 to 10^24 + 1? By restricting the comparison range to finite, as done here, the problem of “course” fine-tuning results [4]. Setting the upper bound to 10^24 + 1 and not considering the other possible values seems arbitrary. Because if the parameter is genuinely a free parameter, it should take an infinite number of values in the denominator, which would lead to a probability of zero. The current status of dealing with these types of problems is quoted above. Even if the math seems tenuous and it affects the conclusion of the argument, perhaps its intuitive appeal is why it is not questioned amongst physicists.
Coming Up Next…
Here, I presented the fine-tuning argument from the perspective of one who believes in fine-tuning with minimal critique. In the next post, I will explain my thesis of why it is minimally scientific. I will also present a Bayesian argument by Jeffreys and Ikeda which will prove that fine-tuning is possible under naturalism. This may sound like a contradiction, but it is not. The constants that we have do seem to allow for life to flourish. But this does not mean that God has set the dial.
Notes
(i) We may think that the conditions of the universe are a garden-variety set of conditions. Maybe life could have evolved in any particular conditions. Presently, we do not know if non-carbon-based life is possible. The point is that life as we know it depends upon the universe’s laws of physics being just so. But is it the other way around; that is, is life fine-tuned for the universe? We can answer this by noticing the arrows of influence. The universe’s values do not depend upon the parameters of life, but life’s parameters depend upon the parameters of the universe. Fine-tuning means that there are precise parameters such that a small deviation would result in a loss of an effect (life). Would changing the parameters in a biological organism affect the universe’s parameters? No. Then the universe is fine-tuned for life, not vice versa.
(ii) There are two types of constants, either physical or mathematical. A physical constant involves an actual measurement, while mathematical constants do not. The value of pi, 3.14 and on, is an example of a mathematical constant that results from the geometric properties of a circle. Physical constants occasionally can be derived mathematically but all have been adjusted through measurement. They further can be divided into either dimensional or dimensionless. The speed of light and the gravitational constant, for example, values vary depending upon the choice of units that are used. When calculating fine-tuning, the preference is to use dimensionless constants, which can be created by taking a ratio of constants. This is because changing the unit can artificially give us large values compared to a different unit. Lastly, these fundamental constants are all a part of the standard model of particle physics and the standard model of cosmology. These constants cannot be derived from anything more fundamental.
(ii) There are of course some who have objected as to which constants should qualify as fine-tuned or to the degree that the fine-tuning exists. Regardless, it is a fact that life as we know it depends upon the constants existing within some range. In the future, we may discover that other elements and states of material energy are conducive to life. However, Victor Stenger, an atheist particle physicist dissenter of fine-tuning, may also be correct. He claims that the constants, as far as I can tell, most if not all, are not as fine-tuned as they are defined to be. Stenger says that “fine-tuning is in the eye of the beholder”. In reviewing his work, it seems plausible, and he provides what may be adequate support. But his peers are to judge, not me. Depending on who we ask, Stenger is either considered mainstream (by atheists) or in the company of “only a handful of dissenters” (by Luke Barnes). In any event, it does not matter because even Stenger says “life depends sensitively on the parameters of our universe.” These constants matter.
(iv) We still need to understand another application for Bayes’ theorem, which allows us to assign probabilities to many observations. The event, such as the different heights of individuals in a population, is now a random variable and can take on many different values, each one having its own probability of occurring. When we display the distribution of the differing heights’ probability, this is known as a probability distribution. Since it is not practical to measure the entire population, we take a few samples from a larger population in order to make generalizations about it. We do this by estimating the parameter, which is supposed to represent the “true value” of the larger population. This approach, which is frequentism, cannot give us the probability of the parameter though, only confidence intervals for where it may exist. For that, we need Bayesian statistics. In this approach, we show our uncertainty of the parameter’s value by making it a random variable of a probability distribution. We then update our uncertainty of the parameter’s value by multiplying the prior distribution times the likelihood distribution and marginalizing the result. The prior is the distribution of the parameter before we observed the data, and the likelihood is the distribution of the observed data, given the parameter.
References:

It doesn’t make sense to speak of the Universe’s physical constants as having been “fine tuned” unless it’s even possible for those constants to have had different values than they actually do. So… you say the Universe was fine-tuned? Cool. What makes you think the Universe’s physical constants could have had different values than they actually do?
Remember that this post is from the perspective of those who believe in fine-tuning. I was clear about this in the beginning [see caption]. You are spoiling my next post, lol. The physicists claim that they could have been different because they have no problem creating universes with different constants. The universes, however, are all dead universes. You are correct though that this is one of two of the weaknesses with the claim of fine-tuning. I will post the problems with the claim hopefully later today.
musing: “The physicists claim that they could have been different because they have no problem creating mathematical simulations of universes with different constants.”
FTFY. And yes, physicists can, indeed, create mathematical simulations of pretty much anything they care too. Given the absence of actual hard data regarding alternate universes, it’s not at all clear why anyone should consider such a mathematical simulation as, you know, evidence of anything at all.
Agreed. Just don’t have a lot of confidence in posting it because there is a very strong consensus that there is nothing special about our particular universe. In other words, it could have been different. I will post it regardless. You can be the judge. I don’t claim that the universe exists out of necessity, but it is very possible that certain mass-energy arrangements favored our constants over some other constants.
The fine tuning argument makes no sense. If some super-being jiggered reality in order to create a petri dish, why is that petri dish so big? Why not just take the simulationist approach and assume we’re looking at parameters in a software simulation run by the almighty for ${reasons}.
I think it was Mark Twain who said: “the puddle says: what a remarkable hole, I fit in it so perfectly, it must have been made for me.”
No doubt Hoyle was a smart fellow, but he wasn’t brave enough to just admit that he was motivated to search for a reason to believe in god.
Good point. I will post the problems with fine-tuning later today. Here I was neutrally taking on the perspective of those who believe in fine-tuning. Remember though that the way we define fine-tuning is that life depends on what the universe’s parameters are. Not the other way around. There is an effect, namely life, that is achieved with these particular values. It doesn’t necessarily mean that an intelligent agent set the dial. But of course that is what is then argued nevertheless.
Marcus Ranum @ # 2: I think it was Mark Twain who said: “the puddle says: what a remarkable hole, I fit in it so perfectly, it must have been made for me.”
If so (which I doubt), then Douglas Adams stole it for his The Salmon of Doubt: Hitchhiking the Galaxy One Last Time.
Marcus @2:
I can’t read minds, but Hoyle’s rejection of the Big Bang (in favour of a steady state universe) seemed to be searching for a reason to deny the existence of a creator god. Worth noting that Einstein initially rejected it as well, although he came around. And noted atheist physicist Steven Weinberg, before he came around, said “The steady-state theory is philosophically the most attractive theory because it least resembles the account given in Genesis”.
IOW, atheists can be as easily distracted by philosophical biases as theists.
One of the things this hinges on is that intelligent life is only possible with our constants. However the correct statement is “intelligent life AS WE KNOW IT is only possible with these constants”. The statement that hydrogen-helium soup doesn’t allow for intelligent life to emerge is just a statement of a limited imagination.
Another problem with a common form of the fine-tuning argument: If the Universal constants were just a tiny bit different, there wouldn’t be [insert whatever here] which means there wouldn’t be stable matter, which means there wouldn’t be life! If there wasn’t stable matter, how do you know that whatever did exist would be incapable of “hosting” self-reproducing phenomena? Perhaps in a universe-without-stable-matter, one of the things there would be was zibbleblorf, and sentient life in that universe could be arguing over how life could possibly exist without zibbleblorf…
Another beef I have with Victor Stenger (I mentioned one in the last post): his dismissal of the hierarchy problem (intimately linked with fine-tuning).
His claim (I can dig it up if required) is that there is no mystery as to why the masses of the fundamental particles are so much smaller than the Planck mass; they are quantum corrections to their original zero masses, therefore inherently small.
Two problems with that:
(1) The mass of the Higgs boson is certainly small wrt the Planck mass, but the quantum corrections to its mass are inherently large.
(2) Heavier fundamental particles tend to decay to lighter ones. That’s why the matter we know is largely made up of the lightest particles; neutrinos, electrons, and u and d quarks. To detect a heavier particle requires experiments which can produce energies on the order of their masses. The energies available to us are many orders of magnitude less than the Planck mass, so to conclude that fundamental particles have inherently small masses is like saying “if I can’t see it, it doesn’t exist”.
I’m glad you brought up Stenger. Luke Barnes, a physicist who believes in design, harshly criticizes Stenger’s work on rebutting fine-tuning in the article “The Fine Tuning of a Universe for Intelligent Life”. If you can suspend your judgment of Barnes’ preference for design, it is very much worthwhile to read as he appears to successfully rebut most of Stenger’s work. There are still many points, however, that I agree with Stenger on. At the very least, he had some interesting ideas.
Stenger was right that the universal constants, such as the speed of light, should not be used to calculate fine-tuning. In fact, Barnes excludes them from his calculation of fine-tuned values. The units could be anything and would thus not give us a “fair” value for fine-tuning. Dimensionless values are preferred.
But then you are left with the problem of defining a prior distribution in such a way that the math will work out in addition to not making the claim of fine-tuning rationally incoherent. I don’t think anyone pulls off both feats, but it is still an intuitive idea; that is, fine-tuning is the probability of a life-permitting universe out of the set of possible universes.
Barnes actually brings up the hierarchy problem when addressing the prior distribution.
From my previous post, I think I was disappointed that Stenger would suggest that radioactive decay is indeterministic. Although you may disagree, I have come to the conclusion that the interpretation of physics, not just quantum physics, is a matter for philosophy. It is still an open question as to how best to interpret a lot of things, especially random phenomena. Stenger may not have been as off as I assumed just because it was contrary to what I believed.
I’ve come to the conclusion that we should clarify, and agree, on what we mean by the terms we use before progress can be made. At this point, the word ‘deterministic’ is essentially meaningless; it’s applied to Many Worlds and de Broglie-Bohm, with wildly different meanings in each case, neither of which satisfies any reasonable (to me, anyway) sense of the word.
Rob, I completely agree.
On a different note, what’s your take on the idea that the universe necessarily happened as opposed to being contingent as in could have been otherwise? The physics community and most philosophers believe that it could have been different. As far as I can tell, is that they do this by claiming that they have no problem creating additional universes with an alternate set of laws by varying the constants. These new laws create universes that are logically possible. That is, they only tell us that the laws are physically possible but not which law is possible. I think we are stretching the imagination a little too much with a logical possibility. They assume that the probability that any given constant can take on is equally probable. But we do not know that this is the case. It is a mathematical assumption of pure indifference (or ignorance). In fact, some physicists at least entertain that mass-energy configurations during the Big Bang may have biased our values to be more likely to occur over some other values. My next post is at a stand still because I do not know how to get around the strong consensus that the universe could have been otherwise.
I like reading about this stuff, but it’s all way above (what was) my pay grade. The only philosophy of physics I’ve consciously engaged in is in coming to a (tentative) preference for the Many Worlds interpretation, simply because it seems to be the only one without ‘spooky action at a distance’. And that’s more an aesthetic choice than an intellectual one.