Wholesome jigsaw puzzle youtuber Karen Kavett recently did a challenge where she assembled a 1000 piece puzzle by selecting 100 pieces at random at a time. For a while, this just looked like a bunch of scattered pieces with only a few connections. But once she had 700 or 800 pieces, the whole puzzle started to come together, despite the gaps.
I found this fascinating, because it is a live demonstration of a concept in physics/math: the percolative transition. This is something I often think about when assembling puzzles.
Percolative theory
The percolative transition describes the point where a jigsaw puzzle changes from mostly disconnected, to mostly connected. It is a phase transition in the same sense as the phase transition between solid, liquid and gas. That is to say, there’s an underlying mathematical theory that governs both the phases of water, and the phases of jigsaw puzzles.
What does it mean for a jigsaw puzzle to be “mostly connected” or “mostly disconnected”? The mathematically precise way to define it involves imagining infinities. Suppose we have a jigsaw puzzle with an infinite number of pieces spreading in all directions. A certain percentage of the pieces are missing (which is to say, each piece has a certain probability of being missing), and the rest of the pieces are available and already in their correct locations.
So here’s the big question: What is the probability that there is at least one cluster of connected puzzle pieces, which is infinite in size?
This is a PhD-level math question, so I’ll just skip to the answer. If less than 59% of the pieces are available, then there cannot be a cluster of infinite size. If more than 59% of the pieces are available, then there must be a cluster of infinite size.
In other words, there’s a sharp change in behavior, that happens at 59%. Or rather, 59.274605079210%, to use physicists’ current best estimate. This dividing line is called the percolation threshold.
Percolative practice
Now if we only have a thousand pieces, that’s somewhat less than infinity. This has the effect of blurring the transition. Rather than having a sharp change at 59%, there will be a more gradual change in the vicinity of 59%.
But, you might have noticed that Karen only managed to connect most of the puzzle once she had 70 or 80% of the pieces. Well, you know, just because you can theoretically connect a lot of pieces together doesn’t mean that you will manage to connect them in practice. Even when you have 100% of the pieces, connecting them all together takes a while.
I still had a few remaining questions about how it really works with a finite number of pieces. So, I wrote a simulation. This simulation creates a 1000 piece jigsaw puzzle, and one by one places pieces into their correct location. I ran the simulation 100 times and collected statistics on the clusters. So here are the results:
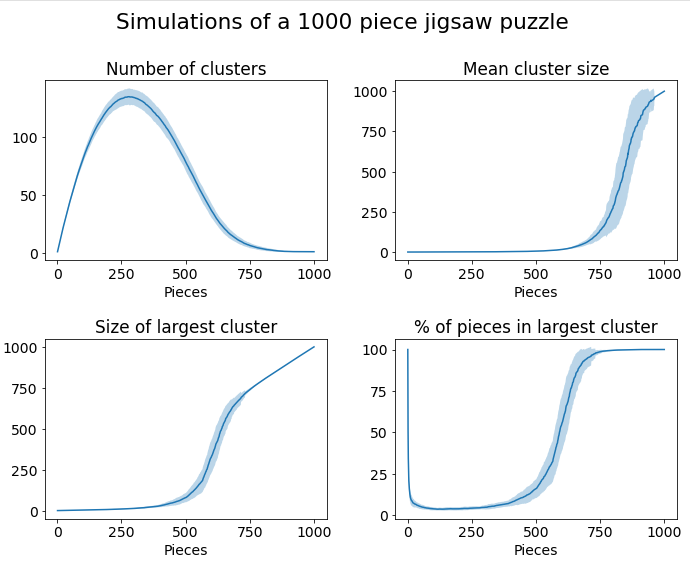
The shaded regions indicate the variance between simulations. I had to implement a disjoint-set data structure for this simulation so I hope you appreciate it.
As you can see, there is a transition between 500 and 750 pieces, where the size of the largest cluster blows up. That’s the percolative transition. By 750 pieces, nearly all the pieces are connected in a single cluster.
I also tried calculating the average cluster size, and I found that this doesn’t blow up until well after the percolative transition. I think that even a few disconnected pieces can really bring the average down. For example, if you have two disconnected pieces, and one cluster with 750 pieces, the average cluster size is reduced to 250 pieces. I think it goes to show that even above the percolation threshold, you will still see a lot of pieces and small clusters that won’t connect with the largest cluster.
The percolative transition is something I think a lot about when solving jigsaw puzzles. If I’m trying complete a certain section of the puzzle, say a patch of sky, I first need to search for the appropriate pieces. Sometimes it’s hard to distinguish sky pieces from other pieces, and I might miss a few. That’s okay; I don’t need to find every sky piece for the section to come together. However, there’s a critical threshold above which the section will come together, and below which it will not. That threshold, mathematically, is 59%, but in practice it’s a bit fuzzier than that, and it might be safer to go higher. It’s worth noting that there is no equivalent magical threshold when assembling edges.
So there’s a super-advanced jigsaw tip for you all. Don’t start assembling a section until you think you have at least 70% of the pieces!
If this article interested you, you might be also be interested in another article I wrote about percolative transitions in Dominion. I’ve also written about the computational complexity of jigsaw puzzles.

How much do the height/width dimensions matter? In the extreme case with a 1 by 1000 you are almost never going to get a single cluster until you place the last piece. (The ‘almost’ is for the 1/500 times that the last piece is an edge piece…)
@robert79,
For infinite jigsaw puzzles, there’s a big distinction between a puzzle that extends infinitely in 2 dimensions vs one that extends infinitely only in one dimension. In the two dimensional case, the transition occurs at 59%, as I said. In the one dimensional case, there is no phase transition–or put another way, the phase transition occurs when you have 100% of the pieces. That’s why my advice about collecting at least 70% of the pieces of a section doesn’t really apply to edges.
For a finite puzzle, I imagine that as it becomes longer and thinner, it starts to behave less like the 2D case and more like the 1D case.
The simulation used standard 25×40 dimensions.