[the fundamentals of the birds and the bees]

Forget all that talk of sexual assault from last time. Instead, pretend I’m an ornithologist.

Wandering past nesting site 84744 M.S. one day, I wonder if a Sexualis Asoltenti has ever flown in and either nested or attempted to nest there. From various studies, I know the odds of that happening are between six and thirteen percent, making it unlikely. Still, I’m just one person; what have other birdwatchers seen? When I get home, I pull up the favourite web forum for local birders and have a look.

I immediately spot a post by Douglas Hugh, who claims to have seen a nesting Sexualis Asoltenti there. What does that do to the odds? Let’s diagram it out.

This rectangle represents every possible situation: that no nest exists, that it was made of discarded twine, that Wile E. Coyote instead threw an Acme Portable Hole in there, and so on. We can slice that space by partitioning it into two, one side containing all possibilities where the nest was built or attempted, the other containing the inverse.
[I should mention these areas aren’t to scale. I’m just focusing on topology here.]

As this rectangle represents every possibility, it also contains scenarios that include Hugh claiming a nest, as well as Hugh not making any such claim. We can further partition the space.

[I should also mention that these boundaries aren’t necessarily accurate. Topology, remember. Also, I wrote this a good three weeks before I saw Jamie’s similar post about Bayes’ Theorem over at SkepChick. Scout’s honour!]

Those previous studies I mentioned represent the area of (A + C) divided by the area of (A + B + C + D).

While we may not know the status of the nest, we do know whether or not Hugh made the claim. Areas C and D are contrary to reality, thus should be dropped from this analysis. The odds of a nest or attempted nest is now the area of A divided by the area of (A + B); in English, that’s the number of instances where Hugh claims a nest, and there is one, as compared to the number of instances where he falsely claims there’s a nest there plus the number of true claims.

As luck would have it, we already have a number to substitute in. Prior research puts the odds of a false nesting claim for Sexualis Asoltenti at between 2-8%; this means that the odds of A / (A + B) are about 92-98%. I’ll take the more conservative value, and say 8% of claims are mistaken, fabricated, or something else. Easy enough.

After figuring all that out, I spot a post from someone named “daufnie_odie.” They claim to have heard a birder mention they’d spotted a nest at 84744 M.S.. No name is given, but the context makes it fairly clear they know this person.

We got lucky last time, because that 8% was for cases where someone claimed they saw a nest or attempted nest, which was exactly the scenario we had. No such luck here, plus there’s a layer of indirection we need to account for. Here’s a first attempt at that:

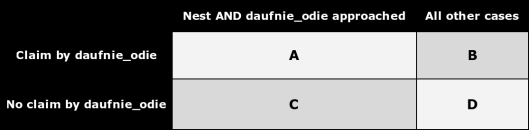On our diagram, the odds of “someone genuinely spots a nest or attempt and mentions it to daufnie_odie” corresponds to the areas where daufnie_odie was approached, A and C, divided by all areas, which is (A + C) / (all). As this box represents all possibilities, and has a total area of one, the odds of the negation of the prior claim (specifically, that there was no nesting, or a false claim, or the news never reaching daufnie_odie), is (1 – (A + C) / (all)) or (B + D) / (all).

Even if that original person saw a nest, though, it’s possible they’d never mention it. We know the first probability, so I’ll put the second at… oh… one third, then multiply the two values together to reach the chance of both events happening.

[Why multiplication? I’ll explicitly cover that in part 3, but if you pay real close attention you’ll get a preview below.]

At this point, I bet a number of you are about to quit in disgust. I just pulled that number out of thin air, and doesn’t that taint the whole enterprise?

If that probability is wildly different from reality, it might. Or, it might not. As I pointed out earlier, if we’re testing the bias of a coin and take a few bad tosses, that could throw off the measurement… but only if we only do a dozen throws. If we do a thousand, it’ll have no significant effect on our final results. Likewise, a bad guess among several good ones will be neutralized, and a lot of fuzzy measurements can combine to create a precise one.

Most importantly, we live in an era of cheap computing. I can run a large number of simulations and check how the parameters change over a wide range of values, giving myself a solid idea of how stable the results are. A little fuzziness is no problem, and who knows? My ad-hoc guess could be bang on the money. This is also handy for anyone who disagrees with my numbers; just plug in your own instead and rerun the analysis.

But back to that. We now need to figure out the odds of daufnie_odie publicly stating their claim, assuming they actually were approached. Maybe they’d forget, or be embarrassed by the situation, but that’s highly unlikely (92%-98% of such claims are legitimate, remember), and this person has some protection by being pseudo-anonymous. I’ll make this probability fairly high, say 95% or so. This corresponds to A / (A + C) in the diagram.

There’s also the possibility that daufnie_odie is making the entire thing up. The pseudo-anonymous argument cuts both ways, also arguing that a false claim is more likely. Nonetheless, an anonymous person that’s careless could be tracked down and held accountable for their words. Given all that, let’s put this probability at an even 50/50. Note that this corresponds to B / (B + D).

Now we can calculate A / (A + B). Multiplying the odds of nesting and this person approaching daufnie_odie, with the odds of daufnie_odie sharing the claim with us, nets us A; multiplying the odds of no nesting or daufnie_odie being approached, with the odds of daufnie_odie making the whole thing up, arrives at B. Put A in the denominator, and the sum of (A + B) in the numerator.

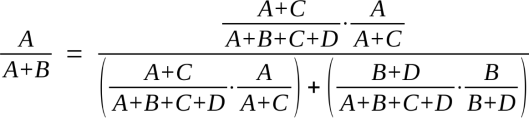That’s a pain to write out, though. Let’s clean things up with some substitution; we’ll call the claim “there was a nest or attempted nest and daufnie_odie was approached by a witness” by the letter “H”, and daufnie_odie’s stating that happened will become “E”. To denote the opposite of a claim, like “daufnie_odie did not state he knew of nesting,” we’ll put a little mark in front of it; in this case, that’d look like “¬E”. To refer specifically to the probability of X happening, we’ll say “P(X)”, and if we talk about the odds of X happening given Y did happen, we’ll write “P(X | Y)”. With these simplifications, the math translates into

Whoops, we’ve accidentally derived a simplified version of Bayes’ Theorem. Ah well, either way we’ve calculated an 11% chance that there was a nest or attempted nest, given daufnie_odie’s post (though as you’ll see later, that number’s a bit naive). As we’re partitioning the probability space, that implies an 89% chance there was no nest or attempt at one.

How do we combine these two accounts together? That’s for part 3…

[HJH 2015-06-09: Minor edits for clarity.]
[HJH 2015-06-19: Emphasized daufnie_odie’s probability would change later.]
[HJH 2015-07-19: Adding a missing link.]