For my monthly repost, I thought I’d reach way back to bring you this post from 2008. I was a physics undergrad back then!
Here’s a physics experiment that you can try yourself right now. It’s fun, I promise.
First, you have to find a small rectangularly-shaped object. Nothing valuable or breakable. A box works fine. A book works too, but you may have to tape the book shut for best results. It is important that there are no square sides on the object. All sides must be rectangles!

Here’s my 3-d model of the box (created with Mathematica). Your own box might differ slightly in its shape, but it should be more or less the same. What are those sticks, you ask? They’re just imaginary lines I drew to mark the three principal axes. If you have an object like a cube or a sphere, one axis is as good as another. But for an object shaped like above, there are three special axes of rotation, called the principal axes.
Now, take the box and toss it up into the air. Give it some spin as you toss it. First, make it spin around the blue line, then the green line, and then the red line.* Observe any differences between the three. I will wait.
…
The first thing you should notice is that it’s harder to spin the box around some axes than others. It should take the most work to spin it around the green line, and the least work to spin it around the blue line. This is because the green axis has the greatest moment of inertia. The blue axis has the smallest moment of inertia. The red axis is somewhere in-between.
The other thing you should observe is that when you try spinning around the red axis, the box spins in a really odd way. After you let go of the box, it will not simply spin around the red axis, but spin and flip around in unexpected ways. If you draw a big “M” on the box, sometimes it will flip around so that you see a “W”.
Why does it do this? The reason is because the principal axes with the greatest and smallest moments of inertia are stable. That is, if you spin around these axes, the object will continue to spin in more or less the same direction, even if you didn’t spin it in exactly the right way. However, the principal axis with the middle moment of inertia is unstable. If you didn’t spin it in exactly the right way, or if air friction pushes the box just a little bit, it will start spinning in all sorts of weird directions.
It’s sort of like carrying a handbag. It’s easy to hang it over your arm, because that is a stable position. But it’s difficult to balance it on your head because that is an unstable position. Stability and instability are important concepts if you want to think like a physicist.
As for why two of the principal axes are stable and the other is not, that is a difficult question with a very mathematical answer. It has to do with three equations called Euler’s Equations.
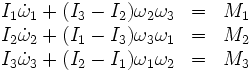
They are a mathematical consequence of Newton’s Laws. I know many of you are looking at that and thinking, “Those equations look so ridiculously complicated!” In this case, you are absolutely right–these equations are ridiculously complicated, even after you learn about differential equations. But even if we don’t solve the equations completely, we can still make qualitative predictions. If you have a cubical or spherical object, its rotation will remain constant. If you have a weirdly shaped object like your box, its rotation is stable around the principal axes of smallest and largest moments of inertia, but unstable around the third principal axis. By testing those predictions, you’ve just done some science!
*For the colorblind: blue goes from upper-left to lower-right, green is vertical, and red goes from lower-left to upper-right.
2020 postscript: I’m so very critical of my writing from 2008. What particularly bothers me is, why didn’t I just choose a more colorblind-friendly communication method in the first place? The experiment’s still great though. Just try it on books, not electronic devices.

A better link for Euler’s rotation equations;
https://en.wikipedia.org/wiki/Euler%27s_equations_(rigid_body_dynamics)
This is one of those times I rue somehow losing my copy of Goldstein. IIRC, he covers this pretty well.
The math isn’t too awful if you consider perturbations to constant angular velocities, and do another time derivative. Then it turns out the perturbations to rotations about the axes with largest and smallest I are oscillating (to first order), while the perturbations to rotations about the intermediate I are exponential (i.e. unstable). It comes down to the sign of the second term in the equations.
If I₁ > I₂ > I₃, then (I₁ − I₃) is the only one which is positive.
Eat the chocolates first.
@Rob Grigjanis
It doesn’t need to be a physics textbook! Any book will do.
I’m not sure if my analysis is the same or different from yours, but here’s how I think of it. Suppose that the book is primarily spinning around one axis (ω3), and the torque (M) is zero. In the short term, we can take ω3 to be a constant (let it be positive WLOG), so we have:
d/dt ω1 ~ (I2 – I3) ω2
d/dt ω2 ~ (I3 – I1) ω1
from which we can derive
d2/dt2 ω1 ~ (I2 – I3)(I3 – I1) ω1
That’s a stable harmonic oscillator if and only if (I2 – I3)(I3 – I1) < 0 This is equivalent to the condition that I3 is either the biggest or smallest principal component of the moment of inertia.
The more complicated part is proving that ω3 doesn’t drift in the long term. I’m not gonna try to prove that one. To be honest back in 2008 I wasn’t capable of this whole analysis at all, I was just bluffing.
Omg Siggy you make actual jokes now? Almost had one of those coffee spraying moments XD
That said, thanks for the interesting experiment, so cool doing science today. here’s an observation on your walkthrough. Though I quickly realised I wasn’t doing it right when you said I was supposed to find the green axis harder, you might want to specify you can’t flip the box on its side before tossing it, like mentioning the green axis has to remain oriented vertically. I’m sure that’s me extremely not thinking like a physicist, but you know. I may not be the only one
Siggy @4: Yeah, that’s the same analysis.
“I’m so very critical of my writing from 2008. What particularly bothers me is, why didn’t I just choose a more colorblind-friendly communication method in the first place? ”
IDK, Perhaps it is because you are human. Your highest calling is within the scope of humanity, and being fallible is part of being human. All the greatest advances have been some combination of hard work learning the problem and working it logically, relaxed idle rumination (bed, bath, bus), intuitive leaps, and boneheaded errors and mistakes that change our perspective, rattle our assumptions, or reveal something new. It is how humans advance. Cut yourself some slack.
These days we have an explanation that involves Space!
@xohjoh2n,
It’s a good explanation, although the way it’s presented seems to imply that spinning around the small axis will also be unstable. If you follow the link to Terry Tao’s explanation, he has an update that explains how when it’s spinning around the small axis, the coriolis effect becomes important.
@9 I had wondered – I thought I must have missed a bit of the earlier explanation on the video. But Tao’s text explanation makes sense, it’s just a pity it isn’t integrated in the video.