This is a repost of an article I wrote way back in 2011.  I’m still proud of figuring this one out.

Out of all the digits, from zero to nine, one is the most common.  This has to do with the log scale.

The log scale captures an important fact that is true of many quantities in life.  Take money for instance.  If you have one dollar, then earning another dollar is great because you’ve doubled your money!  If you have a million dollars, earning another dollar does not make much of a difference.  Small changes matter less the more you already have.

This is true on a log scale too.  On a log scale, 1 is the same distance from 2 as 100 is from 200.  The higher you go up, the more the numbers all get smooshed together.  What does that mean for the digits from zero to nine?

In the above picture, I show a log scale.  And on that scale, I highlighted in blue all the regions where 1 is the first digit of the number.  You should see that the blue regions cover more than one tenth of the log scale.  In fact, they cover about 30%.  And so, if we pick numbers randomly on the log scale, about 30% of those numbers will have 1 as their first digit.

Just for fun, let’s apply this concept on the fundamental constants of nature.  I will compare two hypotheses:

1. The fundamental constants of nature are distributed on a log scale.  About 30% of the constants will have 1 as their first digit, 18% will have 2 as their first digit, and so on.
2. Each digit from 1 to 9 is equally likely to be the first digit of the fundamental constants of nature.

Of course, it could be that both hypotheses are wrong.  It’s difficult to say that these constants are really random.  To talk about randomness, we’d need a whole collection of universes with different sets of fundamental constants so we can do some statistical analysis.  But clearly we have only one universe.  Luckily this one universe has 26 fundamental constants (as far as we know), which may be a big enough collection of numbers to do some statistical analysis.

The caveat is that there is more than one way to choose our 26 fundamental constants!  For instance, the mass of the u quark in planck units could be considered a fundamental constant.  But instead of this constant, we could use a different constant: the ratio of the mass of the u quark to the mass of the electron.  It’s possible I could bias my results by “choosing” the fundamental constants that confirm my hypothesis.

Therefore, I will not choose which constants to use.  I will simply use the list compiled by John Baez and David Black.*  Note that 6 of the constants are unknown, so we’ll have to make do with the remaining 20.

*Baez offers two sets of equivalent constants for the CKM matrix.  I just used the first set.

Results

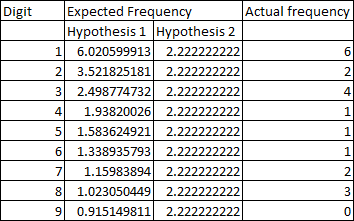
The frequency of first digits more resembles hypothesis 1 than hypothesis 2.  I also tried doing some Bayesian analysis.  If our prior belief is that the likelihood of each hypothesis is 1:1, then this evidence increases the ratio to 15.8:1.  In other words, if we previously thought they were equally likely, then after seeing this evidence, hypothesis 1 is almost 16 times as likely.  As far as evidence goes, this is fairly weak evidence, but you’re not going to get much better with only 20 fundamental constants.

Does this really mean fundamental constants are randomly distributed on a log scale?  Gee, I don’t know.  Probably not really.  What’s your interpretation?