What are fractal mazes?

Fractal Mazes are a type of maze popularized (or invented?) by Mark J. P. Wolf, published in the Mathpuzzle blog in 2003. A fractal maze is a maze that contains nested copies of itself.

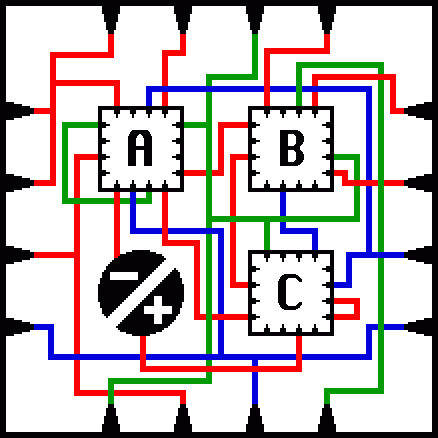
“Small Fractal Maze”. Credit: Mark J. P. Wolf. Source: Mathpuzzle

Fractal Mazes are typically visually represented as a sort of circuit diagram. In the above image, the goal is to find a path between the “+” and “-” by following the colored wires. The wires are color coded in order to clearly indicate where paths cross over/under each other. The three modules, labeled A, B, and C, are each copies of the entire maze. However, the start and finish only exist in the largest copy of the maze. So however deep you go into the fractal, you must eventually climb all the way back up again.

And, I know this is a common point of confusion, since they’re fractals, and you’re thinking of infinity. But traditionally, the solution to a fractal maze is finite. There are infinite paths that you could traverse, but to actually solve a fractal maze, you’re supposed to use a finite number of steps to get from start to finish.

Where are fractal mazes?

You can find a variety of fractal mazes via google search. I was inspired to write this post because someone had pointed me to their repo which lists out every fractal maze they could find online.

Another person pointed me to a browser app they made, which allows you to traverse fractal mazes with a click interface. If you’re trying these for the first time–and assuming the app isn’t taken down–I recommend starting with the easiest one, “Fractal Tomb” (I believe created by Mark J. P. Wolf, also found on Wolfram). Next, give “Circular Maze” a shot. It looks simple, but prepare to be stumped.

My interest in fractal mazes

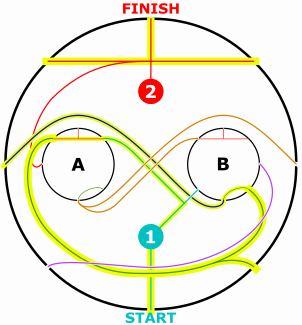
As a once-religious reader of Mathpuzzle, I was entranced by the idea of fractal mazes. Eventually, in 2010, I designed my own fractal maze, retroactively titled “Circular Maze”. And then in 2014 I made two more (also see FTB mirror for the latter).

When I made these, I set out to create mazes that were much simpler than Wolf’s mazes, and yet still challenging to solve. I also went out of my way to distinguish my visual design from that of Wolf, since my perception was that most fractal maze designers would reuse his visual design. However, I admit that Wolf’s visual language can be less confusing than mine. I’ve long wanted to visually tweak my first fractal maze, so I redrew it for this post.

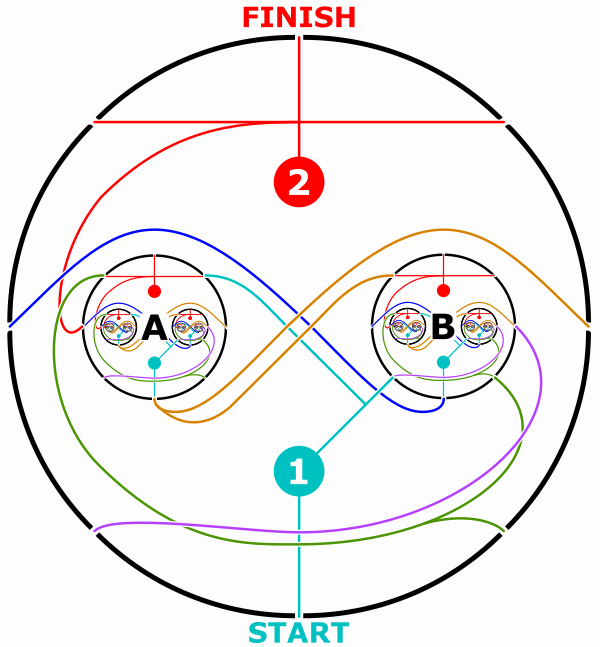
“Circular Maze”, designed by me in 2010, and redrawn by me in 2023. You may share or adapt this image/maze under a Creative Commons Attribution-Noncommercial 4.0 International License. Ask me for the vector graphics.

Apparently “Circular Maze” is such a banger that I’ve seen an article and a masters thesis both use it to explain fractal mazes–although the latter doesn’t credit me properly.  In response, I’m explicitly licensing the maze, under the condition that I am credited properly.

Addressing fractal mazes

It can be easy to get lost in a fractal maze. You might think that’s a desirable property in a maze, but it’s a problem when you’re not sure if you even solved the maze or if you accidentally cheated. To attempt a fractal maze, I recommend taking notes on paper to track where you are in the maze. We can describe your location in the maze using an “address”.

Our address will have two parts. The first part, is the “submaze”, which specifies which copy of the maze you’re currently looking at. The second part we’ll call the “junction”, describing your location within the submaze.

The submaze can be specified with a string of letters. The largest copy of the maze (where we start and end) is assigned the empty string “”. Whenever we go into module A, we append “A” to the string. Whenever we go into module B, we append “B” to the string, and so on. So if we start in the largest submaze, and go into module A followed by module B, we’re now in submaze “AB”. If we exit the current submaze, we pop out the last letter of the string, and that letter tells us which module to exit.

(The submazes are structured like a free monoid. You all remember learning about free monoids in math class, right? I think my math teacher skipped over that one.)

The “junction” part of the address can be specified in any number of ways. One common way would be to label it by one of the endpoints of the path that you’re currently on. Specifically, in Wolf’s Small Fractal Maze, I would assign a number to each of the black triangles, starting from the upper left and going clockwise, number 1 to 16. For example, “+” is at the address C10, because it’s next to the 10th junction within submaze C. The “-” is at the address A12.

Solving fractal mazes

With all that explanation, I hope you’re half as excited about fractal mazes as I am. I hope it does not deflate you when I tell you: fractal mazes are solved! I know they look very difficult, and you definitely can’t solve them with the right hand rule. Nonetheless, there is a simple, fast, and terminating algorithm that you can use to solve any fractal maze. Are you ready to be spoiled?

So here’s the idea. We’re not going to solve the maze in order. Rather, we’re going to put pieces together to create a complete path, starting at the very bottom. Since any solution must be finite, there must be a bottom to the solution, so that’s where we start.

On the very bottom level, we know that we cannot go any deeper into the maze. The only paths that matter are the ones that start and end at the edges of the current copy. (Or, if there’s a path directly from start to finish, that counts too.) Here’s a drawing of the Circular Maze where I’ve highlighted the only paths that matter at the deepest level:

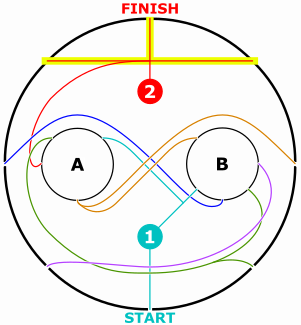
Next we go up one level. We create smaller copies of the maze, but only including the highlighted path, because that’s the only one that matters. Using this new maze, we again highlight any paths that start and end at the edges of the current copy.

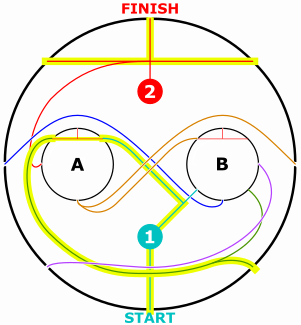
And repeat.  I find it helpful to simplify the highlighted paths when I make smaller copies of the maze.

We continue going up a level, each time highlighting any paths that connect the outer edges of the maze. There are two ways this algorithm can terminate: 1) There’s a path from start to finish, or 2) There is an iteration where no new paths get highlighted. In the former case, you’ve found a solution. In the latter case, you’ve proven that there isn’t a solution.

Technically, this only demonstrates the existence of a solution, and doesn’t explicitly tell you the steps needed to actually solve it. But the algorithm can be slightly modified to address this. Every time you highlight a path, you write down the steps needed to get from one end to the other. It requires some systematic note-taking, but you can do it, you can solve the maze.

We can even put an upper bound on the number of steps this will take. At each step, you must make at least one new connection, or else the algorithm terminates. Therefore, the upper bound is the maximum number of connections that can be made. A single copy of the Circular Maze has 8 exits on the outside, therefore the maximum number of connections that can be made is 7. So there exists a solution that goes no deeper than 7 levels (and in fact there is a solution that only goes down 6).

Designing harder mazes

There you go, fractal mazes are a solved problem. Of course, fractal mazes can still be quite challenging, especially if you try to solve them sequentially from start to end. If you’re interested in designing a fractal maze, you should use the solution to your advantage. You have the secret power to solve your own puzzle, while still knowing that it may be quite challenging to the average solver.

But now that you’ve seen the solution, some of you would-be maze designers are mischievously thinking, is there a way we can defeat the algorithm, and make a more difficult maze? I got a couple ideas just for you!

The first idea is a simple one. In a traditional fractal maze, you start and end in the largest copy of the fractal maze. Suppose instead that the solver is allowed to start in any copy of the maze, with the restriction that they must end in the very same copy. Tricky!

My second idea takes a lot more work. Remember the rule that any solution to the fractal maze must be finite? What if we allowed infinite solutions? I will discuss this idea further in a future post.