As a reminder, I’m open to requests to discuss any popular physics articles or videos, to append to my “I read popular physics” series. This video was not requested, but was shared by a friend of a friend a while back, and I have things to say about it.
Recently, the YouTube Channel Veritasium posted a video “Why the Speed of Light* Can’t be Measured”. The video argues that all measurements of the speed of light involve sending light in one direction, and waiting for it to come back. However, the light could theoretically be traveling faster in one direction than the other. It seems we are not directly measuring the speed of light, but rather the average speed of light in both directions. The constant speed of light in all directions is a matter of theoretical convention rather than empirical fact.
In the Facebook thread where I first saw the video shared, many people were incredulous. As for myself, I immediately understood the argument from the title, and immediately agreed that it was correct. However, I feel the video is misleading, as it does not explain why there is a theoretical convention that the speed of light is constant. And by doing so, I feel it misses the point of relativity theory.
Special Relativity is a theory proposed by Einstein in 1905, and frequently taught to physics undergraduates in their first or second year. The purpose of Special Relativity is to explain the results of the Michelson-Morley experiment in 1887, which measured the speed of light in different directions. Technically, it did not directly measure the speed of light, but instead measured the time it takes for light to travel in one direction and back again. Thus, the experiment couldn’t really separate the eastward and westward speeds of light. It could, however, measure the difference between the east/west speed and the north/south speed. And the difference appeared to be zero.
By this point, light was already understood to be a wave. And just as other waves travel through some medium (e.g. sound waves travel through air, water waves travel through water), it was expected that light too would travel through a medium. Like other waves, it was expected that light would have the same speed in all directions—but only relative to its medium. If we conduct an experiment in the lab, this lab is standing on a rotating planet orbiting the sun, so it’s implausible that the lab is always staying still relative to light’s medium.
This is all stuff you can learn from popular accounts of relativity theory. What the popular accounts often leave out is the math. We have mathematical equations for light, which are the very same equations governing the electricity and magnets: Maxwell’s equations. Physicists will often describe Maxwell’s equations as beautiful in their simplicity, but I’m just going to paste them here and let the readers judge that for themselves.
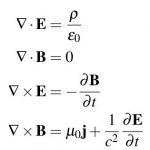
You can even derive the speed of light from these equations.
Using pure math, it is possible to transform Maxwell’s equations to a different reference frame—for example, deriving new equations that would hold from the perspective of our moving lab. This mathematical transformation shows that Maxwell’s equations can only be correct in one reference frame—in all other reference frames, it is at most approximately correct. The goal of the Michelson-Morley experiment was to precisely measure which was the reference frame where Maxwell’s equations were correct. Insted, they found that Maxwell’s equations appear to be correct in all reference frames, a mathematical impossibility.
Special Relativity allows Maxwell’s equations to be correct in all reference frames by making two modifications: First, we must adjust Maxwell’s equations. Second, we must expand our understanding of what it means to transform between reference frames. Previously, we only imagined transformations that would affect position (x), leaving time (t) unchanged.
Special Relativity brings our attention to transformations that affect both position and time.
(a, b, c, and d are arbitrary constants)
Depending on your choice of transformation, you may find that Maxwell’s equations change, which is to say that the original equations are no longer correct. This allows for the speed of light to go faster in the eastward direction than the westward direction, for instance. However, Einstein identified a special set of transformations, known as Lorentz transformations, which would preserve Maxwell’s equations. Furthermore, he supposed that all physical laws would be preserved by Lorentz transformations.
Special Relativity established Lorentz transformations as the default transformation between reference frames in physics. It is also the most natural transformation, insofar as we would like to be able to just write down Maxwell’s equations–used not just to predict the speed of light but also the behavior of ordinary electronics–without taking into consideration the latitude, time of day, and time of year. This is, however, just a convention. You could perform some non-Lorentz transformation, resulting in an unconventional set of spacetime coordinates where light travels at different speeds in different directions. This would make Maxwell’s equations a lot more complicated, and sort of defeat the point of relativity theory. But you could do it! Veritasium is technically correct.
In fact, there’s another convention that Veritasium seems to have completely taken for granted. That is, conventionally “t” represents time as it is subjectively experienced by a motionless observer. But we could choose a transformation that stretches or shrinks time. We could even reverse time, or swap time and space. You could make the speed of light faster or slower in all directions. But, normally we don’t do that, because it would be kind of a silly exercise. What I’m saying, is that Veritasium’s video feels like a similarly silly exercise.
But I will say one thing. If you ever want to study General Relativity, you may want to get used to general coordinate transformations. General Relativity describes the behavior of gravity using curved space-time. It’s a much more advance topic, typically being taught to PhD students rather than undergraduates. I actually never studied General Relativity! One of these days I’ll go through Carroll’s Spacetime and Geometry, but it’s hard to find the time.

Siggy: the name you want is Veritasium, not Veritaserum.
… all measurements of the speed of light involve sending light in one direction, and waiting for it to come back.
Eh? Many of the early measurements of c involved calculating when, e.g., a given moon of Jupiter would occult a particular star, and timing exactly when the light from that star would disappear and reappear as seen from Earth. With repeated measurements as sidereal alignments allow, that method provided consistent answers for light traveling from a full circle of directions (albeit only within the plane of the ecliptic).
Or am I just displaying, again, the polymathic ignorance of a non-physicist/astronomer/mathematician?
@DonDueed, thanks for the correction
@Pierce R. Butler,
I’m not familiar with the measurement that you’re describing, but presumably at some point it makes assumptions about orbital motion (or other laws of physics) that are no longer correct under non-Lorentzian transformations.
Maybe I’m misunderstanding you, but that makes it sound like he looked for transformations that would preserve Maxwell’s equations. That’s not the approach he took in On the Electrodynamics of Moving Bodies, in which he first derived coordinate transformations from the constancy of c, after defining his synchronization.
He then applies that result to Maxwell’s equations (the two involving time derivatives of the fields) to derive the transformation of the fields which would preserve the equations.
Pierce @2: If you’re talking about Rømer’s method, that involved looking at data for eclipses of Io by Jupiter. See this answer in physics stack exchange.
@Rob Grigjanis #4,
Yeah, that’s probably a more accurate characterization as far as the order of derivation goes. But I’m not trying to describe the order of derivation. Einstein did identify a special set of transformations, those transformations do preserve Maxwell’s equations in their modified form. Yes, he derived the modified form after he described Lorentz transformations.
If we’re considering general transformations, why restrict ourselves to linear ones like you present? After all, Einstein’s first postulate of relativity alone only guarantees that space and time transform via linear fractional transformations with common denominator. To cut those down to an arbitrary linear transformation, you need to specify that spacetime is homogeneous. There’s a great proof in Fock’s GR textbook. If we’re talking about relaxing the second postulate, why not also consider non-homogeneous in addition to non-isotropic spacetime?
I dunno much about fizzix, but I did spot one booboo in the video: surely Hippolyte Fizeau did not pronounce his name “Hippo Light”.
I’d recommend Dirac’s General Theory of Relativity. Very readable, and only 69 pages!
Pierce @8: I stopped caring very much about mispronouncing foreign names after hearing Italian soccer commentators pronounce ‘Hughes’ as ‘Yooks’.