After writing my post on the randomization of a deck of cards, I became more curious about this topic. In a deck of 52 distinct cards, there are 52x51x50…x3x2x1 possible arrangements. This is written in the mathematical notation 52! and is an enormous number. Perfect randomization of a deck means that starting with any given arrangement, after the shuffling process, all possible arrangements are equally likely and have the probability 1/52!. One can also think of it as saying that after the randomization process, a card that started out in any given position should be equally likely to be found in any of the 52 positions.
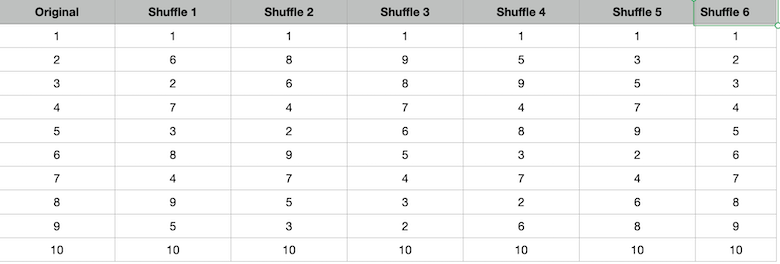
I learned that magicians for some of their tricks use the fact that shuffles do not guarantee randomizing of the deck, and so was curious to see how that might work. To illustrate this very simply, I started with a deck of just ten cards numbered 1 through 10 in order. I then cut the deck in two so that one half contained 1through 5 and the other half contained 6 through 10. Then I imagined a perfect riffle shuffle where the cards from each side are dropped one at a time alternately. You then get the order shown under the heading Shuffle 1.