Russian Hacking and Bayes’ Theorem, Part 1

I’m a bit of an oddity on this network, as I’m pretty convinced Russia was behind the DNC email hack. I know both Mano Singham and Marcus Ranum suspect someone else is responsible, last I checked, and Myers might lean that way too. Looking around, though, I don’t think anyone’s made the case in favor of Russian hacking. I might as well use it as an excuse to walk everyone through using Bayes’ Theorem in an informal setting.

(Spoiler alert: it’s the exact same method we’d use in a formal setting, but with more approximations and qualitative responses.)

[Read more…]

About Damn Time

Ask me to name the graph that annoys me the most, and I’ll point to this one.538's graph of Trump's popularity, as of May 25th, 2017.

Yes, Trump entered his presidency as the least liked in modern history, but he’s repeatedly interfered with Russian-related investigations and admitted he did it to save his butt. That’s a Watergate-level scandal, yet his approval numbers have barely changed. He’s also pushed a much-hated healthcare reform bill, been defeated multiple times in court, tried to inch away from his wall pledge, and in general repeatedly angered his base. His approval ratings should be negative by now, but because the US is so polarized many conservatives are clinging to him anyway.

A widely held tenet of the current conventional wisdom is that while President Trump might not be popular overall, he has a high floor on his support. Trump’s sizable and enthusiastic base — perhaps 35 to 40 percent of the country — won’t abandon him any time soon, the theory goes, and they don’t necessarily care about some of the controversies that the “mainstream media” treats as game-changing developments. […]

But the theory isn’t supported by the evidence. To the contrary, Trump’s base seems to be eroding. There’s been a considerable decline in the number of Americans who strongly approve of Trump, from a peak of around 30 percent in February to just 21 or 22 percent of the electorate now. (The decline in Trump’s strong approval ratings is larger than the overall decline in his approval ratings, in fact.) Far from having unconditional love from his base, Trump has already lost almost a third of his strong support. And voters who strongly disapprove of Trump outnumber those who strongly approve of him by about a 2-to-1 ratio, which could presage an “enthusiasm gap” that works against Trump at the midterms. The data suggests, in particular, that the GOP’s initial attempt (and failure) in March to pass its unpopular health care bill may have cost Trump with his core supporters.

At long last, Donald Trump’s base appears to be shrinking. This raises the chances of impeachment, and will put tremendous pressure on Republicans to abandon Trump to preserve their midterm majority. I’m pissed the cause appears to be health care, and not the shady Russian ties or bad behavior, but doing the right thing for the wrong reason is still doing the right thing. It also fits in nicely with current events.

According to the forecast released Wednesday by the nonpartisan Congressional Budget Office, 14 million fewer people would have health insurance next year under the Republican bill, increasing to a total of 19 million in 2020. By 2026, a total of 51 million people would be uninsured, roughly 28 million more than under Obamacare. That is roughly equivalent to the loss in coverage under the first version of the bill, which failed to pass the House of Representatives.

Much of the loss in coverage would be due to the Republican plan to shrink the eligibility for Medicaid; for many others—particularly those with preexisting conditions living in certain states—healthcare on the open marketplace would become unaffordable. Some of the loss would be due to individuals choosing not to get coverage.

The Republican bill, dubbed the American Health Care Act, would also raise insurance premiums by an average of 20 percent in 2018 compared with Obamacare, according to the CBO, and an additional 5 percent in 2019, before premiums start to drop.

So keep an eye on Montana’s special election (I’m writing this before results have come in); if the pattern repeats from previous special elections, Republicans will face a huge loss during the 2018 midterms, robbing Trump of much of his power and allowing the various investigations against him to pick up more steam.

Daryl Bem and the Replication Crisis

I’m disappointed I don’t see more recognition of this.

If one had to choose a single moment that set off the “replication crisis” in psychology—an event that nudged the discipline into its present and anarchic state, where even textbook findings have been cast in doubt—this might be it: the publication, in early 2011, of Daryl Bem’s experiments on second sight.

I’ve actually done a long blog post series on the topic, but in brief: Daryl Bem was convinced that precognition existed. To put these beliefs to the test, he had subjects try to predict an image that was randomly generated by a computer. Over eight experiments, he found that they could indeed do better than chance. You might think that Bem is a kook, and you’d be right.

But Bem is also a scientist.

Now he would return to JPSP [the Journal of Personality and Social Psychology] with the most amazing research he’d ever done—that anyone had ever done, perhaps. It would be the capstone to what had already been a historic 50-year career.

Having served for a time as an associate editor of JPSP, Bem knew his methods would be up to snuff. With about 100 subjects in each experiment, his sample sizes were large. He’d used only the most conventional statistical analyses. He’d double- and triple-checked to make sure there were no glitches in the randomization of his stimuli. Even with all that extra care, Bem would not have dared to send in such a controversial finding had he not been able to replicate the results in his lab, and replicate them again, and then replicate them five more times. His finished paper lists nine separate ministudies of ESP. Eight of those returned the same effect.

One way to attack an argument is to merely follow its logic. If you can find it leads to an absurd conclusion, the argument must have been flawed even if you cannot find the flaw. Bem had inadvertently discovered a “reductio ad absurdum” argument against contemporary scientific practice: if proper scientific procedure can prove ESP exists, proper scientific procedure must be broken.

Meanwhile, at the conference in Berlin, [E.J.] Wagenmakers finally managed to get through Bem’s paper. “I was shocked,” he says. “The paper made it clear that just by doing things the regular way, you could find just about anything.”

On the train back to Amsterdam, Wagenmakers drafted a rebuttal, to be published in JPSP alongside the original research. The problems he saw in Bem’s paper were not particular to paranormal research. “Something is deeply wrong with the way experimental psychologists design their studies and report their statistical results,” Wagenmakers wrote. “We hope the Bem article will become a signpost for change, a writing on the wall: Psychologists must change the way they analyze their data.”

Slate has a long read up on the current replication crisis, and how it links to Bem. It’s aimed at a lay audience and highly readable; I recommend giving it a click.

P-hacking is No Big Deal?

Possibly not. simine vazire argued the case over at “sometimes i’m wrong.”

The basic idea is as follows: if we use shady statistical techniques to indirectly adjust the p-value cutoff in Null Hypothesis Significance Testing or NHST, we’ll up the rate of false positives we’ll get. Just to put some numbers to this, a p-value cutoff of 0.05 means that when the null hypothesis is true, we’ll get a bad sample about 5% of the time and conclude its true. If we use p-hacking to get an effective cutoff of 0.1, however, then that number jumps up to 10%.

However, p-hacking will also raise the number of true positives we get. How much higher it gets can be tricky to calculate, but this blog post by Erika Salomon gives out some great numbers. During one simulation run, a completely honest test of a false null hypothesis would return a true positive 12% of the time; when p-hacking was introduced, that skyrocketed to 74%.

If the increase in false positives is balanced out by the increase in true positives, then p-hacking makes no difference in the long run. The number of false positives in the literature would be entirely dependent on the power of studies, which is abysmally low, and our focus should be on improving that. Or, if we’re really lucky, the true positives increase faster than the false positives and we actually get a better scientific record via cheating!

We don’t really know which scenario will play out, however, and vazire calls for someone to code up a simulation.

Allow me.

My methodology will be to divide studies up into two categories: null results that are never published, and possibly-true results that are. I’ll be using a one-way ANOVA to check whether the average of two groups drawn from a Gaussian distribution differ. I debated switching to a Student t test, but comparing two random draws seems more realistic than comparing one random draw to a fixed mean of zero.

I need a model of effect and sample sizes. This one is pretty tricky; just because a study is unpublished doesn’t mean the effect size is zero, and vice-versa. Making inferences about unpublished studies is tough, for obvious reasons. I’ll take the naive route here, and assume unpublished studies have an effect size of zero while published studies have effect sizes on the same order of actual published studies. Both published and unpublished will have sample sizes typical of what’s published.

I have a handy cheat for that: the Open Science Collaboration published a giant replication of 100 psychology studies back in 2015, and being Open they shared the raw data online in a spreadsheet. The effect sizes are in correlation coefficients, which are easy to convert to Cohen’s d, and when paired with a standard deviation of one that gives us the mean of the treatment group. The control group’s mean is fixed at zero but shares the same standard deviation. Sample sizes are drawn from said spreadsheet, and represent the total number of samples and not the number of samples per group. In fact, it gives me two datasets in one: the original study effect and sample size, plus the replication’s effect and sample size. Unless I say otherwise, I’ll stick with the originals.

P-hacking can be accomplished a number of ways: switching between the number of tests in the analysis and iteratively doing significance tests are but two of the more common. To simply things I’ll just assume the effective p-value is a fixed number, but explore a range of values to get an idea of how a variable p-hacking effect would behave.

For some initial values, let’s say unpublished studies constitute 70% of all studies, and p-hacking can cause a p-value threshold of 0.05 to act like a threshold of 0.08.

Octave shall be my programming language of choice. Let’s have at it!

(Template: OSC 2015 originals)
With a 30.00% success rate and a straight p <= 0.050000, the false positive rate is 12.3654% (333 f.p, 2360 t.p)
Whereas if p-hacking lets slip p <= 0.080000, the false positive rate is 18.2911% (548 f.p, 2448 t.p)

(Template: OSC 2015 replications)
With a 30.00% success rate and a straight p <= 0.050000, the false positive rate is 19.2810% (354 f.p, 1482 t.p)
Whereas if p-hacking lets slip p <= 0.080000, the false positive rate is 26.2273% (577 f.p, 1623 t.p)

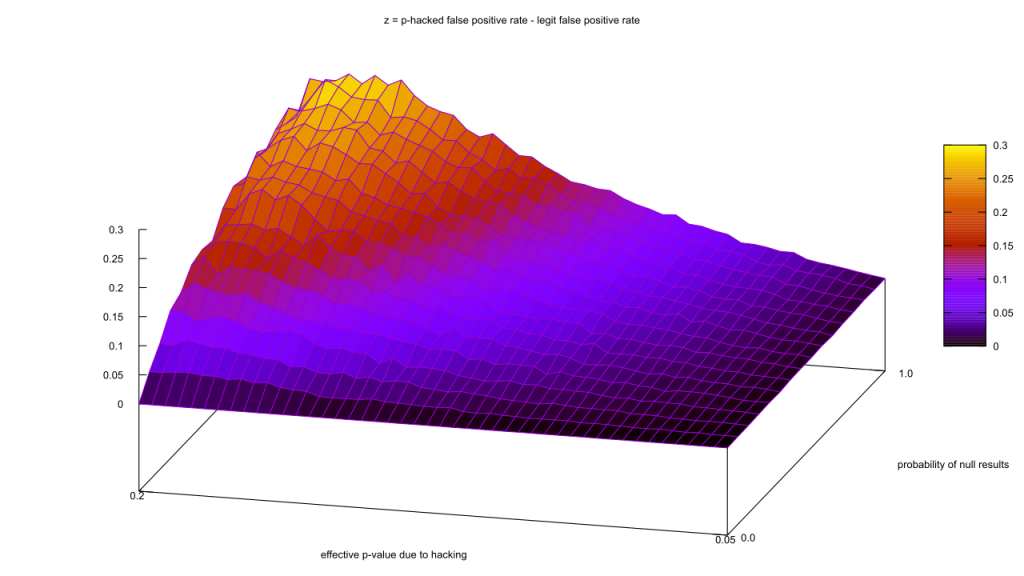
Ouch, our false positive rate went up. That seems strange, especially as the true positives (“t.p.”) and false positives (“f.p.”) went up by about the same amount. Maybe I got lucky with the parameter values, though; let’s scan a range of unpublished study rates from 0% to 100%, and effective p-values from 0.05 to 0.2. The actual p-value rate will remain fixed at 0.05. So we can fit it all in one chart, I’ll take the proportion of p-hacked false positives and subtract it from the vanilla false positives, so that areas where the false positive rate goes down after hacking are negative.

How varying the proportion of unpublished/false studies and the p-hacking amount changes the false positive rate.

There are no values less than zero?! How can that be? The math behind these curves is complex, but I think I can give an intuitive explanation.

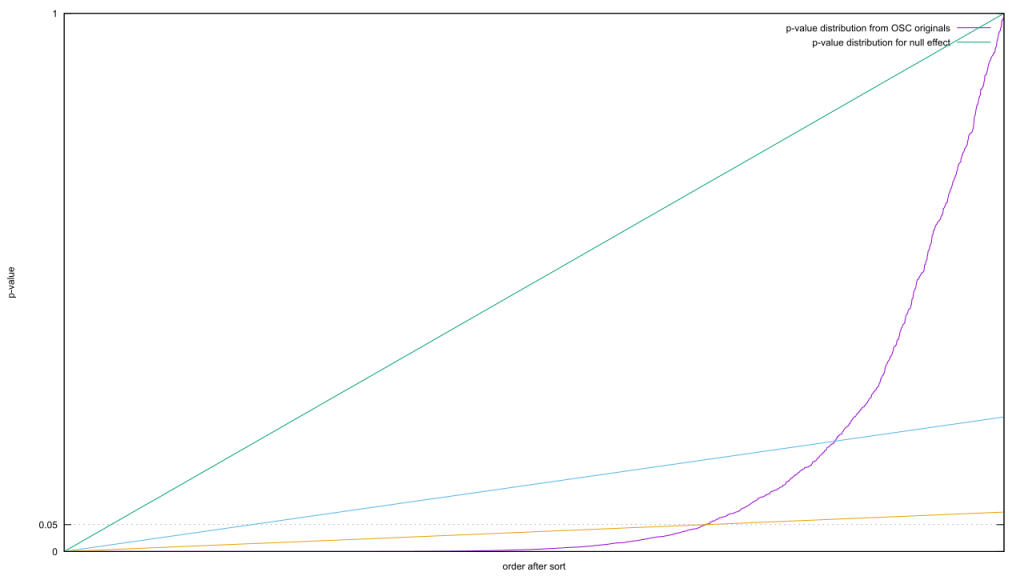Drawing the distribution of p-values when the result is null vs. the results from the OSC originals.The diagonal is the distribution of p-values when the effect size is zero; the curve is what you get when it’s greater than zero. As there are more or less values in each category, the graphs are stretched or squashed horizontally. The p-value threshold is a horizontal line, and everything below that line is statistically significant. The proportion of false to true results is equal to the proportion between the lengths of that horizontal line from the origin.

P-hacking is the equivalent of nudging that line upwards. The proportions change according to the slope of the curve. The steeper it is, the less it changes. It follows that if you want to increase the proportion of true results, you need to find a pair of horizontal lines where the horizontal distance increases as fast or faster in proportion to the increase along that diagonal. Putting this geometrically, imagine drawing a line starting at the origin but at an arbitrary slope. Your job is to find a slope such that the line pierces the non-zero effect curve twice.

Slight problem: that non-zero effect curve has negative curvature everywhere. The slope is guaranteed to get steeper as you step up the curve, which means it will curve up and away from where the line crosses it. Translating that back into math, it’s guaranteed that the non-effect curve will not increase in proportion with the diagonal. The false positive rate will always increase as you up the effective p-value threshold.

And thus, p-hacking is always a deal.

But Everything Worked Out, Right?

The right person won in the recent France election, but the outcome worries me. The polls badly underestimated his win.

The average poll conducted in the final two weeks of the campaign gave Macron a far smaller lead (22 percentage points) than he ended up winning by (32 points), for a 10-point miss. In the eight previous presidential election runoffs, dating back to 1969, the average poll missed the margin between the first- and second-place finishers by only 3.9 points.

That should be a warning flag to the French to take less stock in their polls and weight unlikely outcomes as more likely. It’s doubtful they will, though, because everything turned out all right. That’s no slam against the French, it’s just human nature. Take the 2012 US election:

Four years ago, an average of survey results the week before the election had Obama winning by 1.2 percentage points. He actually beat Mitt Romney by 3.9 points.

If that 2.7-point error doesn’t sound like very much to you, well, it’s very close to what Donald Trump needs to overtake Hillary Clinton in the popular vote. She leads by 3.3 points in our polls-only forecast.

That was Harry Enten of FiveThirtyEight four days before the 2016 US election, four days before Clinton fell victim to a smaller polling error. Americans should have done back in 2012 what the French should do now, but they didn’t. Even the betting markets figured Clinton would sweep, an eerie mirror of their French counterparts.

Overall, there are a higher number of bets on Ms Le Pen coming out on top, than Brexit or Donald Trump – even though the odds are much lower, according to the betting experts.

The moral of the story: don’t let a win go to your head. You might miss a critical bit of data if you do.

Gimmie that Old-Time Breeding

Full disclosure: I think Evolutionary Psychology is a pseudo-science. This isn’t because the field endorses a flawed methodology (relative to the norm in other sciences), nor because they come to conclusions I’m uncomfortable with. No, the entire field is based on flawed or even false assumptions; it doesn’t matter how good your construction techniques are, if your foundation is a banana cream pie your building won’t be sturdy.

But maybe I’m wrong. Maybe EvoPsych researchers are correct when they say every other branch of social science is founded on falsehoods. So let’s give one of their papers a fair shake.

Ellis, Lee, et al. “The Future of Secularism: a Biologically Informed Theory Supplemented with Cross-Cultural Evidence.” Evolutionary Psychological Science: 1-19. [Read more…]

Everything Is Significant!

Back in 1939, Joseph Berkson made a bold statement.

I believe that an observant statistician who has had any considerable experience with applying the chi-square test repeatedly will agree with my statement that, as a matter of observation, when the numbers in the data are quite large, the P’s tend to come out small. Having observed this, and on reflection, I make the following dogmatic statement, referring for illustration to the normal curve: “If the normal curve is fitted to a body of data representing any real observations whatever of quantities in the physical world, then if the number of observations is extremely large—for instance, on an order of 200,000—the chi-square P will be small beyond any usual limit of significance.”

This dogmatic statement is made on the basis of an extrapolation of the observation referred to and can also be defended as a prediction from a priori considerations. For we may assume that it is practically certain that any series of real observations does not actually follow a normal curve with absolute exactitude in all respects, and no matter how small the discrepancy between the normal curve and the true curve of observations, the chi-square P will be small if the sample has a sufficiently large number of observations in it.

Berkson, Joseph. “Some Difficulties of Interpretation Encountered in the Application of the Chi-Square Test.” Journal of the American Statistical Association 33, no. 203 (1938): 526–536.
His prediction would be vindicated two decades later.

[Read more…]

Stop Assessing Science

I completely agree with PZ, in part because I’ve heard the same tune before.

The results indicate that the investigators contributing to Volume 61 of the Journal of Abnormal and Social Psychology had, on the average, a relatively (or even absolutely) poor chance of rejecting their major null hypotheses, unless the effect they sought was large. This surprising (and discouraging) finding needs some further consideration to be seen in full perspective.

First, it may be noted that with few exceptions, the 70 studies did have significant results. This may then suggest that perhaps the definitions of size of effect were too severe, or perhaps, accepting the definitions, one might seek to conclude that the investigators were operating under circumstances wherein the effects were actually large, hence their success. Perhaps, then, research in the abnormal-social area is not as “weak” as the above results suggest. But this argument rests on the implicit assumption that the research which is published is representative of the research undertaken in this area. It seems obvious that investigators are less likely to submit for publication unsuccessful than successful research, to say nothing of a similar editorial bias in accepting research for publication.

Statistical power is defined as the odds of failing to reject a false null hypothesis. The larger the study size, the greater the statistical power. Thus if your study has a poor chance of answering the question it is tasked with, it is too small.

Suppose we hold fixed the theoretically calculable incidence of Type I errors. … Holding this 5% significance level fixed (which, as a form of scientific strategy, means leaning over backward not to conclude that a relationship exists when there isn’t one, or when there is a relationship in the wrong direction), we can decrease the probability of Type II errors by improving our experiment in certain respects. There are three general ways in which the frequency of Type II errors can be decreased (for fixed Type I error-rate), namely, (a) by improving the logical structure of the experiment, (b) by improving experimental techniques such as the control of extraneous variables which contribute to intragroup variation (and hence appear in the denominator of the significance test), and (c) by increasing the size of the sample. … We select a logical design and choose a sample size such that it can be said in advance that if one is interested in a true difference provided it is at least of a specified magnitude (i.e., if it is smaller than this we are content to miss the opportunity of finding it), the probability is high (say, 80%) that we will successfully refute the null hypothesis.

If low statistical power was just due to a few bad apples, it would be rare. Instead, as the first quote implies, it’s quite common. That study found that for studies with small effect sizes, where Cohen’s d was roughly 0.25, their average statistical power was an abysmal 18%. For medium-effect sizes, where d is roughly 0.5, that number is still less than half. Since those two ranges cover the majority of social science effect sizes, that means the typical study has very low power and thus a small sample size. Instead, the problem of low power must be systemic to how science is carried out.

In this fashion a zealous and clever investigator can slowly wend his way through a tenuous nomological network, performing a long series of related experiments which appear to the uncritical reader as a fine example of “an integrated research program,” without ever once refuting or corroborating so much as a single strand of the network. Some of the more horrible examples of this process would require the combined analytic and reconstructive efforts of Carnap, Hempel, and Popper to unscramble the logical relationships of theories and hypotheses to evidence. Meanwhile our eager-beaver researcher, undismayed by logic-of-science considerations and relying blissfully on the “exactitude” of modern statistical hypothesis-testing, has produced a long publication list and been promoted to a full professorship. In terms of his contribution to the enduring body of psychological knowledge, he has done hardly anything. His true position is that of a potent-but-sterile intellectual rake, who leaves in his merry path a long train of ravished maidens but no viable scientific offspring.

I know, it’s a bit confusing that I haven’t clarified who I’m quoting. That first paragraph comes from this study:

Cohen, Jacob. “The Statistical Power of Abnormal-Social Psychological Research: A Review.” The Journal of Abnormal and Social Psychology 65, no. 3 (1962): 145.

While the second and third are from this:

Meehl, Paul E. “Theory-Testing in Psychology and Physics: A Methodological Paradox.” Philosophy of Science 34, no. 2 (1967): 103–115.

That’s right, scientists have been complaining about small sample sizes for over 50 years. Fanelli et. al. [2017] might provide greater detail and evidence than previous authors did, but the basic conclusion has remained the same. Nor are these two studies lone wolves in the darkness; I wrote about a meta-analysis of 16 different power-level studies between Cohen’s and now, all of which agree with Cohen’s.

If your assessments have been consistently telling you the same thing for decades, maybe it’s time to stop assessing. Maybe it’s time to start acting on those assessments, instead. PZ is already doing that, thankfully…

More data! This is also helpful information for my undergraduate labs, since I’m currently in the process of cracking the whip over my genetics students and telling them to count more flies. Only a thousand? Count more. MORE!

… but this is a chronic, systemic issue within science. We need more.

Double-Dipping Datasets

I wrote this comment down on a mental Post-It note:

nathanieltagg @10:
… So, here’s the big one: WHY is it wrong to use the same dataset to look for different ideas? (Maybe it’s OK if you don’t throw out many null results along the way?)

It followed this post by Myers.

He described it as a failed study with null results. There’s nothing wrong with that; it happens. What I would think would be appropriate next would be to step back, redesign the experiment to correct flaws (if you thought it had some; if it didn’t, you simply have a negative result and that’s what you ought to report), and repeat the experiment (again, if you thought there was something to your hypothesis).

That’s not what he did.

He gave his student the same old data from the same set of observations and asked her to rework the analyses to get a statistically significant result of some sort. This is deplorable. It is unacceptable. It means this visiting student was not doing something I would call research — she was assigned the job of p-hacking.

And both the comment and the post have been clawing away at me for a few weeks, when I’ve been unable to answer. So let’s fix that: is it always bad to re-analyze a dataset? If not, then when and how?

[Read more…]

BBC’s “Transgender Kids, Who Knows Best?” p1: You got Autism in my Gender Dysphoria!

This series on BBC’s “Transgender Kids: Who Knows Best?” is co-authored by HJ Hornbeck and Siobhan O’Leary. It attempts to fact-check and explore the many claims of the documentary concerning gender variant youth. You can follow the rest of the series here:

  1. Part One: You got Autism in my Gender Dysphoria!
  2. Part Two: Say it with me now…
  3. Part Three: My old friend, eighty percent
  4. Part Four: Dirty Sexy Brains

 

Petitions seem as common as pennies, but this one stood out to me (emphasis in original).

The BBC is set to broadcast a documentary on BBC Two on the 12th January 2017 at 9pm called ‘Transgender Kids: Who Knows Best?‘. The documentary is based on the controversial views of Dr. Kenneth Zucker, who believes that Gender Dysphoria in children should be treated as a mental health issue.

In simpler terms, Dr. Zucker thinks that being/querying being Transgender as a child is not valid, and should be classed as a mental health issue. […]

To clarify, this petition is not to stop this program for being broadcast entirely; however no transgender experts in the UK have watched over this program, which potentially may have a transphobic undertone. We simply don’t know what to expect from the program, however from his history and the synopsis available online, we can make an educated guess that it won’t be in support of Transgender Rights for Children.

That last paragraph is striking; who makes a documentary about a group of people without consulting experts, let alone gets it aired on national TV? It helps explain why a petition over something that hadn’t happened yet earned 11,000+ signatures.

Now if you’ve checked your watch, you’ve probably noticed the documentary came and went. I’ve been keeping an eye out for reviews, and they fall into two camps: enthusiastic support…

So it’s a good thing BBC didn’t listen to those claiming this documentary shouldn’t have run. As it turns out, it’s an informative, sophisticated, and generally fair treatment of an incredibly complex and fraught subject.

… and enthusiastic opposition …

The show seems to have been designed to cause maximum harm to #trans children and their families. I can hardly begin to tackle here the number of areas in which the show was inaccurate, misleading, demonising, damaging and plain false.

… but I have yet to see someone do an in-depth analysis of the claims made in this specific documentary. So Siobhan is doing precisely that, in a series of blog posts.
[Read more…]