See part 1
Dissonance in music is analogous to conflict in a story. Dissonance sounds “unpleasant” in the same way that conflict is unpleasant to the characters within the story, but then it would be an odd to have a story without any conflict. The opposite of dissonance is called consonance. Music commonly alternates between dissonance and consonance–creating tension, and then resolving it.
Conventional musical theory comes with a bunch of ideas about what’s consonant or dissonant. 400 cents, the major third, is considered consonant; 300 cents, the minor third, is considered dissonant. There’s some physical basis for these ideas, but arguably a lot of it has to do with tradition. 300 cents is more dissonant than 400 cents because that’s the meaning we’ve absorbed from our musical culture.
When you go outside the usual tuning system, musical tradition offers less guidance on what’s more or less dissonant. So this is the part of my intro to xenharmonic theory where I discuss a theory of dissonance that is independent of musical tradition.
Roughness theory
If we want to talk about dissonance on a psychophysical basis, apart from the idiosyncracies of musical tradition, it’s worth giving it a different name. In the literature, it’s often called roughness. Roughness is based on the idea of dissonance, and some of the literature will simply refer to it as dissonance, but I will maintain a distinction between the two concepts.
The theory of roughness was first described by Plomp & Levelt in 1965. It was based on musically untrained individuals’ perception of dissonance when listening two pure tones played simultaneously. Perception of dissonance was maximized at a particular interval, circa 100 cents. Intervals that were larger or smaller than 100 cents were perceived as less dissonant. So roughness refers to the sensation we have when there are two pure tones about 100 cents apart.
As I explained in part 1, a pure tone is a perfect sine wave, but a real musical instrument will contain higher harmonics. So roughness theory says that when two notes are played together, roughness may occur between their respective harmonics.
For example, suppose we have two notes at 0 cents and 300 cents. The fifth harmonic of the first note is at 2786, while the fourth harmonic of the second note is 2400+300=2700 cents. These are 86 cents apart, so that creates a roughness sensation. The magnitude of this roughness depends on the amplitude of the harmonics, which in turn depends on the instrument.
The interval of roughness
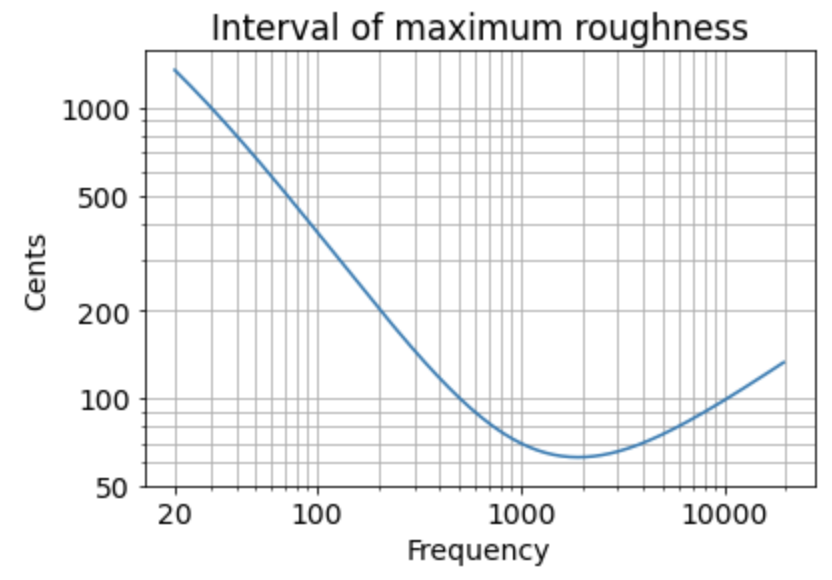
I said that roughness is maximized at an interval of around 100 cents, but let me be more precise. In the lower end of the hearing range, the roughness interval is larger; and in the higher end of the hearing range, the roughness interval is smaller.
I’d like to quantify that further. According to Plomp and Levelt, roughness is maximized at about 25% of the critical bandwidth. The critical bandwidth is a psychoacoustical concept that I won’t cover in this introduction, but I looked up an empirical formula for the critical bandwidth, which gives us the following expression:
Interval of maximum roughness = 23.5 + 0.0005613*f^(3/2) Hz = 1200*log2(1+23.5/f + 0.0005613*f^(1/2)) cents
where f is frequency in Hz.
I’ve never seen anyone plot this function in cents, so let me be the first:
Roughness and beating
As I explained in part 1, when you hear two notes of similar frequency, it causes a beating frequency equal to the difference in frequencies. So if we play two notes with an interval that maximizes roughness, we’ll hear beating, and the beating will have frequency of 23.5 + 0.0005613*f^(3/2) Hz.
Over a large range of frequencies, the beating is pretty close to 20 Hz. 20 Hz is special, because it’s near the lower limit of human hearing. This suggests a certain interpretation of roughness: Roughness occurs when the beating frequency is too fast to keep track of, but slow enough that it’s outside our hearing range.
It’s actually not about integer ratios
In part 3, I will be discussing tuning theory, which places a great deal of emphasis on “nice” integer frequency ratios, such as 4:3 or 5:4. Integer frequency ratios cause the harmonics to line up, reducing beating, and creating local minima in roughness. However, before we get there, I’d first like to explain why integer ratios are not the be-all end-all of music.
Let’s go through the exercise of applying roughness theory to the 5:4 ratio. So we have two notes at 0 and 386 cents. But if you take the 6th harmonic of the lower note, that’s 3102 cents, and the 5th harmonic of the upper note is 2786+386=3172 cents. That’s a 70 cent difference between the two harmonics, and that produces a sensation of roughness. And you could say, well the 6th and 5th harmonics of those notes aren’t very strong, so maybe the roughness is small enough that we can ignore it. But if that were the case, there would be no point to using the 6:5 ratio, whose main benefit is eliminating the roughness between the 6th and 5th harmonics. Integer ratios don’t eliminate roughness, they just reduce it.
This analysis is still missing something: inharmonicity. For real instruments, the harmonics are not exact integer multiples of the fundamental, there’s some deviation. To get a sense of scale, I looked up the inharmonicity of an upright piano. In the middle range, the fifth harmonic may be off by 25 cents! Another source for a different upright piano said it was 15 cents–so it’s not even consistent. So if you want to line up the fourth and fifth harmonics of two notes, you wouldn’t even tune them to perfect integer ratios, you’d have to offset the interval to account for inharmonicity.
Besides, outside of integer frequency ratios, there’s another effective way to reduce roughness. You can have two notes which are several octaves apart. The lower note will have higher harmonics, but the amplitude of those harmonics will drop off, and if the notes are sufficiently far apart there will be relatively little interference between harmonics.
Error tolerance in integer ratios
When we’re aiming for integer frequency ratios, there’s a lot of tolerance for error. Chiefly, in practice, people just can’t tell when the frequency ratios are off. You can tell if you have musical training, and if conditions are controlled. But, most people don’t have musical training, and most conditions aren’t controlled. If we worry about a few cents here and there, it’s the musical version of talking about angels on pinheads. It can be fun, but it really just doesn’t matter.
This can be illustrated by understanding how much we stretch integer ratios in common practice. In standard western tuning, we use 400 cents to approximate the 5:4 ratio, which is 14 cents off from the exact 5/4 ratio at 386 cents. This is considered a consonant ratio even though it’s 14 cents sharp. And some instruments, such as the piano, get tuned to be pretty close to 400 cents. Other instruments, such as the human voice, vary more wildly but probably center around 386. Many instruments, like woodwinds, can’t really tune individual notes, so some notes are sharp and some notes are flat. And then there’s the aforementioned inharmonicity. And most people don’t even notice all these details. It’s fine. Music is fine.
In my experience, programming electronic instruments is one of the few contexts where a few cents can make a difference. If you think about it, these are maximally controlled conditions; also I’m the composer, so I’m paying close attention, and I have musical training. Under these conditions, do I tune instruments just right? No, actually, I often deliberately detune instruments by up to 10 cents for a fuller and more lively sound. And it’s not just me, I learned this from tutorials on instrument design. Which goes to show, even when roughness or beating are noticeable, they’re not necessarily undesirable.
Don’t get me wrong, integer ratios are important to think about, but they don’t need to be exact. Music theory ought to be grounded in what we actually perceive, lest it turn into numerology.
Next part: Tuning theory

Leave a Reply