Like many physicists, I have a fondness for simple physical systems that behave in unexpected ways. Here’s a demo known as “Kapitza’s pendulum”.

For those who didn’t watch the video, it shows an ordinary pendulum attached to a motor. Then the motor starts moving up and down 58 times per second. While the motor is running, the pendulum stands upright, and stays upright even when knocked to the side.

Kapitza’s Pendulum is easily understood by anyone with a degree in physics. But for everyone else, here’s an explanation that could be understood with high school physics.

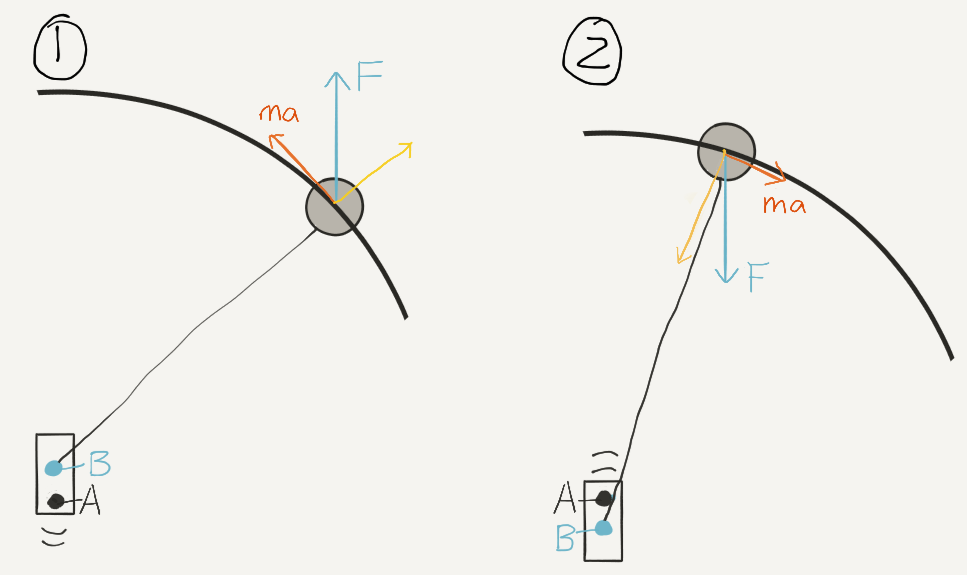
Here I show the pendulum in two different positions. Point A is fixed, while the pendulum is attached to point B. So diagram (1) shows the pendulum when the motor is at its highest point, and diagram (2) shows when the motor is at its lowest point. Note that the diagrams are not to scale.

The accelerating motor can be considered to be applying a fictitious force* to the pendulum. On the diagram, this force is labeled as F. F goes up when the motor is accelerating down, and goes down when the motor is accelerating up. Normally, F would cancel itself out, in the long run.

However, F can be split into two components:

One component (in yellow) can be ignored, because it is perpendicular to the circular arc of the pendulum. Basically, the yellow component is cancelled out by the forces that keep the pendulum rigid.

The other component (in orange, labeled as ma), shows how the pendulum accelerates in response to F. As you can see in the diagram, the orange component is larger in (1) than it is in (2). So F does not cancel out in the long run. Instead, there is a net force pushing the pendulum upwards.

The result is a stable inverted pendulum.

*Most people are familiar with another fictitious force, the centrifugal force. High school teachers sometimes claim these forces aren’t real, but in higher physics we learn that they are real enough.