Most people are probably aware of the Higgs boson, long predicted, and recently observed by the Large Hadron Collider in 2012. The Higgs boson is was predicted by the Higgs mechanism, which is a theory that endows certain particles with mass.
Now, you might be wondering why I, a researcher in superconductivity, am talking about particle physics. In fact, the Higgs mechanism started out as a theory of superconductivity, and was soon imported to particle physics. I leave the historical details to your encyclopedia of choice.
To understand the superconductor/particle physics connection, consider the question: For which particles does the Higgs mechanism generate mass?
In particle physics, the Higgs mechanism generates mass for the W and Z particles, the mediators of the Weak force. The reason it’s called the Weak force is because it’s so short range, which is a consequence of the W and Z having mass. To my understanding, other elementary particles derive their mass from their interaction with the Weak force. (not quite correct, although link is correct. See comments for details)
!["Of these four forces, there's one we don't really understand." "Is it the weak force or the strong--" "It's gravity." Transcript: There are four fundamental forces between particles: (1) Gravity, which obeys this inverse square law: F= G m1 m2 over d squared. (2) Electromagnetism, which obeys this inverse-square law: F = k q1 q2 over d squared and also Maxwell's equations (3) The Strong nuclear force, which obeys, uh... well, umm... it holds protons and neutrons together. It's strong. And (4) the Weak force. It [mumble mumble] radioactive decay [mumble mumble]--And those are the four fundamental forces!](https://freethoughtblogs.com/atrivialknot/files/2016/06/xkcd_fundamental_forces.png)
From xkcd. Hover text: “Of these four forces, there’s one we don’t really understand.” “Is it the weak force or the strong–” “It’s gravity.” Accurate.
In superconductors, the Higgs mechanism generates mass for the electromagnetic field. This causes the electromagnetic field to be short range. Thus, if you apply an external electric or magnetic field, it will not penetrate into a superconductor of any appreciable size. The zero magnetic field is called the Meissner effect; the zero electric field leads to zero resistance current.
That’s the short explanation of what the Higgs mechanism does, but I wanted to explain how it works. Also, I wanted to try out this new doodling software…
The Mexican Hat potential
The Higgs field begins with the so-called Mexican Hat potential. It’s called that based on its shape:
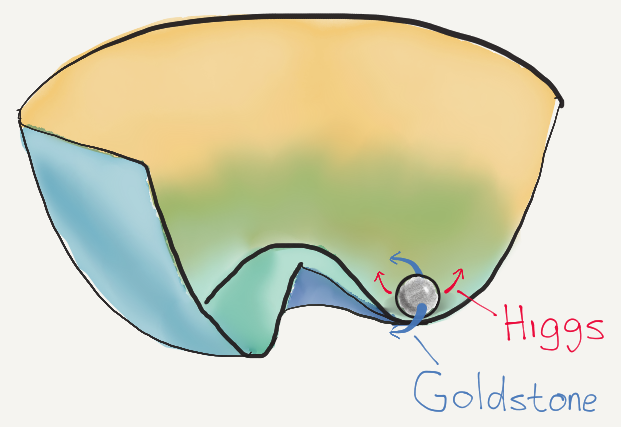
Figure 1. Images mine. Use only with attribution.
The sphere here is not a physical sphere, but represents the value of the field. If the sphere is at the center of the potential, then the field is zero. If the sphere is off-center, then the field is nonzero. The sphere prefers to roll downhill, and in this landscape that means lying somewhere off-center along the circular valley. The significance of the Mexican Hat potential is that it’s circularly symmetric, and yet the value of the field is nonzero.
In superconductivity, the field in question is the superconducting order parameter, and it was long known that it existed in a landscape like the one shown above. In particle physics, the field is the Higgs field, the existence of which was a premise of the theory. Note the distinction between the Higgs mechanism, the Higgs field and the Higgs boson. As I’ll explain below, Higgs bosons are excitations in the Higgs field.
What is a field?
“Field” is a technical term in physics that means something that exists everywhere in space. So you have to imagine that at every point in space, there exists a little sphere rolling around a Mexican Hat. Rather than drawing a bunch of hats, I’m going to abstractify them into circles.

Figure 2.
In the field shown above, the value is nearly the same everywhere, but there’s a small oscillation in the amplitude (i.e. the distance of the sphere from the center of the Mexican Hat potential). This oscillation is the Higgs boson, which I had also labeled in Figure 1.
I had also indicated a second boson in Figure 1, the Goldstone boson. This is an oscillation in the direction of the field, like so:
 Figure 3.
Figure 3.
Ironically, the Higgs boson is mostly unimportant to the Higgs mechanism, an incidental biproduct of the Mexican Hat potential. It’s really the Goldstone boson which is important, as well as a third boson, called the gauge boson. The Goldstone boson and gauge boson are both massless, but the Higgs mechanism is all about how they combine to create a single massive particle.
What is mass?
At this point, I should disentangle a few distinct concepts of mass:
1. How hard is it to push the object?
2. How strongly does the object interact with gravity?
3. What is the energy of the object at rest?
#1 and #2 are equivalent to each other (according to Einstein’s theory of General Relativity), but more accurately describe energy, not mass. When we talk about the mass generated by the Higgs mechanism, we’re talking about #3.
“Wait!” you say. “I thought mass and energy were the same!” You may be familiar with Einstein’s equation E = mc2, which relates energy (E) to mass (m) and the speed of light (c). But Einstein’s equation is only true for an object at rest. In general, energy also depends on an object’s momentum (p). The more general equation is E2 = (mc2)2 + (pc)2. To determine an object’s mass, you just need to find the energy when its momentum is zero.
It’s actually not that hard to generate mass from a massless particle. For instance, you can put light (which is massless) in a mirror box. And since the light bounces back and forth, its average momentum is zero, but its energy is still nonzero. Voila, mass! Most of the mass of protons and neutrons is generated this way. That isn’t how the Higgs mechanism works though.
The last thing I want to show, before Part 2, is why the Higgs boson is inherently massive, and the Goldstone boson inherently massless. According to quantum mechanics, momentum is inversely proportional to wavelength. A boson with zero momentum is equivalent to an oscillation with infinite wavelength. So to determine the mass of a boson, we calculate its energy in the limit of infinite wavelength.
 Figure 4.
Figure 4.
In Fig. 4, I show a Higgs boson with infinite wavelength. The energy of the boson is nonzero, because it requires some energy to push that sphere up the brim of the Mexican Hat. Therefore the Higgs boson is inherently massive, even before we introduce the Higgs mechanism.
 Figure 5.
Figure 5.
In Fig. 5, I show a Goldstone boson with infinite wavelength. At each point in space, the Higgs field is rotated by a certain amount. This makes no difference whatsoever, and it’s as if there is no Goldstone boson at all. This Goldstone boson has zero energy and thus Goldstone bosons are inherently massless.
Because superconductors are described by a Mexican Hat potential, it was predicted early on that they would have a massless Goldstone boson. However, experimentalists were unable to find such a thing. So the origin story of the Higgs mechanism was as an explanation for how Goldstone bosons acquired mass in superconductors.
Coming up next, an explanation of gauge bosons and mass generation.

The elementary fermions (quarks, leptons) get their masses from a Yukawa interaction with the Higgs field. The symmetry breaking, and consequent non-zero vacuum expectation value of the Higgs, gives rise to the mass terms for these particles.
@Rob Grigjanis,
I could have been mistaken about how the Higgs generates mass for Fermions (and in any case, it’s not covered by this post or in part 2 either). Do you (or anyone else) know enough about it that you could help me correct it?
A few things confuse me, first that Matt Strassler’s explanation seems dissimilar to the Yukawa interaction explanation–which could mean that he’s just explaining it in an abstruse way, that there are two alternate mechanisms, or that one of the sources is mistaken. The second thing that confuses me is the way that the Wikipedia article on the Yukawa interaction characterizes the Higgs mechanism as a way to generate mass for fermions, where the article on the Higgs mechanism characterizes it as a way to generate mass for bosons. I suspect that they are two distinct mechanisms, but that physicists often elide the distinction.
Siggy, I’ll try to get back to you later this afternoon. There’s soccer on (Italy vs Spain and then England vs Iceland), and I’m one of the poor benighted fools who follow it religiously. Quickly; Strassler actually pictures the Yukawa interaction without naming it!
This part actually discusses the fermion sector.
Same mechanism, but you have to add the Yukawa terms “by hand”, so to speak. Then the observed masses become a measure of the Yukawa coupling strengths between the Higgs and the fermion in question.
I’ll look more closely at Strassler’s piece later.
To be clearer, you add the gauge-invariant Yukawa terms to the symmetric pre-breaking Lagrangian. The Higgs mechanism then gives the fermion mass terms after breaking, via the non-zero vacuum expectation value of the Higgs. Of course, the Yukawa couplings are then parameters which have to be determined by experiment, but I wouldn’t call this a distinct mechanism.
Thanks, Rob for your explanations.
The way I explain the Higgs mechanism in part 2 (which is scheduled for next week) is closely tied to the way that gauge bosons act as the “connection” of the Higgs field. This framing made the most sense to me in analogy to superconductors, but it’s not very natural to extend it to fermions. Which, I suppose, speaks to the value of framing the mechanism in multiple ways.
I don’t think the fermion stuff is important for your purposes anyway.
By the way, I really liked the scholarpedia entry on the Higgs mechanism*. Scholarpedia is a good resource for physics.
*Called the Englert-Brout-Higgs-Guralnik-Hagen-Kibble mechanism there, maybe cuz the author was Tom Kibble.
I have borrowed your picture of the Mexican hat potential for one of my documents. I have attributed it to your site, with the URL in a footnote. If this is not all right, please contact me.
@John O’Neall,
No problem. Thanks for letting me know.