At March Meeting, there was a fascinating talk about the phase diagram of ribbons.  Yeah, just like the solid/liquid/gas phase diagram of water!  Their paper is called Helicoids, Wrinkles, and Loops in Twisted Ribbons (see on PRL if you have journal access).  Here’s the first figure:

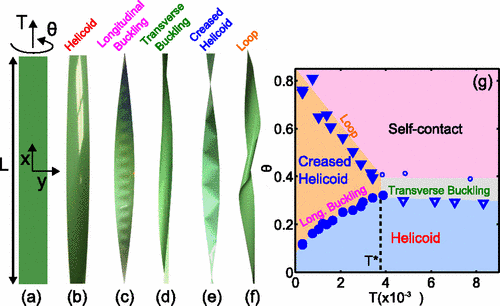
Left side: many possible responses of a stretched and twisted ribbon.  Right side: a phase diagram of the ribbon as a function of stretching force (T) and twisting angle (θ).

The researchers claim, “Our results can be used to develop functional structures”.  I don’t know what that means, but I’m already sold!  I am going to replicate this experiment!

The researchers use a rather fancy ribbon made up of polyethylene terephthalate.  I’m fresh out of that, so I cut out a strip of origami paper.  I gave it a little twist, and behold:

You can already see a bit of the zig-zag crease pattern.  This is what the researchers call a creased helicoid.  Here’s another picture with the creases traced out:

The zig-zags aren’t quite perfect, but I suppose that was to be expected given my budget (I couldn’t even afford the CT Scanner).  Origami paper isn’t an ideal ribbon, since it has some geometrical stiffness, as well as memory of past creases.

For my next experiment, I twisted the ribbon further and pulled a little harder.

This phase is called transverse buckling.  If you take a vertical cross-section down the middle, you find that the ribbon is bent.  In the zoomed image below, you can see that the white dot is not directly between the two black dots, but below them.  That’s what buckling is.

Please try this at home!  You can try a variety of materials, although paper was the only thing I found that could make a creased helicoid.  I bet you could do it with kids too!  It would show them how complex properties emerge from simpler ones.  That’s what condensed matter physics is all about.