By “logic puzzle”, I don’t just mean puzzles involving logic, but rather a specific genre of puzzles, whose most famous types are Sudoku and Picross. There are many other types of such puzzles, and creators of logic puzzles can create entirely new types, if they are so inclined. If you’re not sure what I’m talking about, or if you’re just interested in finding logic puzzles, at the bottom of this post I’ve included a list of places you can find them.
I’m fairly good at logic puzzles. I’ve done the US Puzzle Championship for over a decade, and I placed in the top 25 once? So not like top-of-the-world good, but decent. And I’m a generalist, which is to say that relatively speaking I’m not very good with Sudoku, and I do better with other types of puzzles, including entirely new types.
My goal here is to overexplain my understanding of logic puzzles, and solving strategy. I am not confident that this is actually helpful to someone trying to get better at solving logic puzzles, but that’s not really the point. The point is to explicitly describe what would otherwise only be understood intuitively.
Assumptions
The first assumption that we take for granted, is that a logic puzzle has a unique solution. And when we say “unique solution”, that can be broken down into two separate assumptions, first that there is at least one solution, and the second that there is no more than one solution.
Every assumption I state is meant to be broken. There are logic puzzles that do not have unique solutions. For example, puzzles in the video game The Witness look superficially similar to logic puzzles, but often have multiple solutions, and it still works as a puzzle game. You could argue that the non-uniqueness of solutions distinguishes it from the logic puzzle genre, but I won’t waste any time arguing over the boundaries of the genre.
But by default, it is assumed that every puzzle has a unique solution. If a puzzle has multiple solutions, or god forbid no solution at all, this might be considered a violation of trust the solver has in the creator. The Witness gets away with it because it sits near the genre’s borders.
And yet, traditionally the solver is not meant to assume a unique solution as part of their logical deductions. If the solver does make that assumption, it’s sometimes regarded as cheating. (In my experience though, calling it “cheating” is misleading, because it’s rarely a good way to get ahead, it’s mostly a good way to make mistakes.) Instead, the solver is supposed to prove there is a unique solution by systematically eliminating all possibilities except one.
Even though you’re not supposed to assume a unique solution, knowing that your proof will eventually conclude that there is a unique solution has a huge impact on the strategy. One does not solve puzzles in The Witness by systematically eliminating all possibilities except one, because you know it’s often impossible to do that. Instead, the strategy in The Witness is to eliminate what you can, and use heuristics to try things out.
Even when a logic puzzle has a unique solution, this does not universally imply that the systematic elimination strategy is the best one. Numberlink is a notable exception, obeying entirely different conventions. The best strategy for Numberlink involves assuming there is a unique solution, and using lots of heuristics. So basically, when I discuss solving strategy below, it does not apply to The Witness, nor Numberlink; and I leave open the possibility that there are other puzzles for which the strategy fails.
The solution space
Logic puzzles often ask you to fill each square with a number, or color each square black or white, or draw lines between some of the points. This defines a solution space for each puzzle. For example, in Sudoku, there are 81 squares, each of which can have one of 9 digits. So there are 9^81 possible solutions, and you need to eliminate all but one of those.
You can think of these solutions as being organized in a tree (as in the data structure). The root of the tree has 9 children, and each of those children has 9 more children, and each one of those has 9 children, and so on until the tree has 9^81 leaves corresponding to each solution. The nodes in the first row may correspond to the upper left square; the first child indicates that this square has a “1”, the second indicates that it has a “2” and so on. But there are many ways to organize the solutions into a tree; for example the first row might instead correspond to the second square of the puzzle.

So suppose that you’ve deduced that the upper left square has a “1”. You’ve already eliminated 8*9^80 of the possible solutions, leaving a solution space that is still impossibly large, and yet quite a bit smaller than before. That’s the sort of step that you want to make: not eliminating solutions one at a time, but rather organizing the tree such that you can eliminate entire branches of the tree at a time.
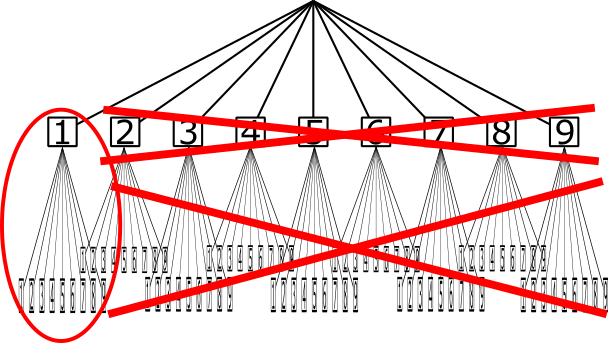
Guess and disprove
Now, the plain way to summarize the previous section, is that you should solve a Sudoku by deducing one number at a time. And that’s almost correct! But in the general case, you don’t have the luxury. Sometimes you need to go deeper, like literally deeper into the tree.
Rather than eliminating 8 of the nodes in the first row, you might only be able to eliminate 7. That leaves you with two separate branches. One branch has a unique solution, the other branch does not have any solution. So now you get to work on these two branches as if they were separate puzzles. Eventually, you may prove a contradiction in one of the branches, and so you can eliminate that one and focus entirely on the other branch.
Here’s what that means in terms of actually solving the Sudoku. You pick a square, and identify all the possible digits it could hold. For each possibility, you then generate a new puzzle, which assumes that possibility to be correct. You then work on each puzzles separately, until you prove that all but one of them has a contradiction. So if you can’t tell if a square is a 1 or a 9, you can try it both ways, proceeding until you prove that one of them is impossible. I’m calling this the “guess and disprove” strategy.
Guess and disprove is a recursive strategy. Once you’ve split the puzzle into two separate puzzles, you might then split each of those puzzles into two more, and each of those into two more, and so on. Not that you would usually do this, but you can in principle.
I’m going to make a few assertions about the “guess and disprove” strategy, which I haven’t definitively proven, but which I am confident are true:
- Guess and disprove is a slow strategy.
- Every logic puzzle, without exception, can eventually be solved with guess and disprove.
- If a type of logic puzzle is NP, that implies that guess and disprove is a necessary strategy in at least some puzzles.
- Every type of logic puzzle should be assumed to be NP until proven otherwise.
Basically, guess and disprove is a blunt instrument, a strategy of last resort, but you cannot avoid it entirely.
Deductive rules
Let’s take a step back and discuss the simpler kind of deduction, where you deduce one digit at a time. Generally, to make simple deductions, you follow a set of deductive rules. Note that every type of logic puzzle is defined by a set of rules. For example, the rules of Sudoku are:
- Place a number from 1 to 9 in each empty cell.
- Each row, column, and 3×3 block bounded by bold lines (nine blocks) contains all the numbers from 1 to 9.
But one should distinguish the rules that define the type of logic puzzle from the deductive rules. Deductive rules are basically a set of instructions that you can follow to fill in squares. For example, here are two of the simplest deductive rules for Sudoku:
- Consider a particular square. If you can eliminate 8 of the digits by looking in the rest of the row, column, and 3×3 block, then the square must be filled with the last digit.
- Consider a particular digit, and a particular 3×3 block. If you can eliminate the possibility that the digit is contained in 8 of the 9 squares, then the digit must be in the last square.
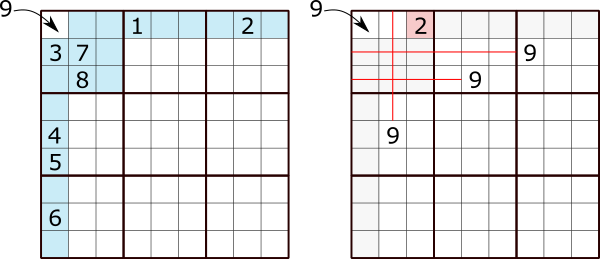
Illustrations of the two rules above
These aren’t the only deductive rules that are useful in Sudoku, but they’re your bread and butter.
Every puzzle type has a set of deductive rules, which aren’t necessarily obvious at the outset, but which may be hidden. Every new type of logic puzzle has a learning curve as you identify useful deductive rules.
So far, I’ve broken down my approach to solving logic puzzles into three parts: Identifying deductive rules, applying deductive rules, and using guess and disprove. Next, I’ll discuss some practical details.
Identifying deductive rules
Some deductive rules are easy to identify. For example, if a puzzle says:
Black cells cannot be linked to be 2×2 square or larger. (Nurikabe)
And if you’ve deduced that three of the squares in a 2×2 box are black, then you can deduce that the fourth is white. It’s simple and direct.
But then you get much more complicated rules, such as:
Connect adjacent dots with vertical or horizontal lines to make a single loop. The loop never crosses itself and never branches off. (Slitherlink)
This leads to a wealth of deductive rules that are not immediately obvious. For example, this implies the rule that every dot is connected to exactly 0 or 2 line segments. It implies that every square can be assigned a color, either green for inside the loop, or blue for outside the loop, and these colors obey certain rules. It implies that if you draw any rectangle, the loop must cross the boundaries of this rectangle an even number of times.
How do you come up with rules like this? It’s hard to say, but one way is to just apply guess and disprove, and look for patterns in the results. Once you’ve identified a pattern, and proven to yourself that it always holds, you can create a deductive rule as a shortcut. It’s not a deterministic process, and requires some creativity.
Another thing to point out, is that not all deductive rules are about deducing the state of a single square. For instance, a common deductive rule in Sudoku, is to deduce that a certain digit must be in exactly one of two squares. And then there are a lot of techniques to represent this knowledge on paper, and additional rules for how to make further deductions.
And when you think about it, there’s no upper bound to the complexity of these rules. For example, a hand-crafted logic puzzle may be contrived to make use of a deductive rule that is so specific that it would never appear except on purpose. But there is a practical limit, which is how many rules you can identify, keep in your head, and how effectively you can use them.
Applying deductive rules
Once you have a set of deductive rules in your toolkit, actually trying to apply all of them everywhere could take a very long time. So which rules do you try applying first, where do you apply them, and when do you give up and switch to guess and disprove?
These are tough questions. I think you need to learn from experience which deductive rules to check first, where to apply them most effectively, and so on. For example, among the two deductive rules that I stated for Sudoku, I almost always start with the second one. I don’t know how you would know that, except through experience.
A few general tips: It’s a lot faster if you have a way to check a rule on a bunch of places at once. For instance, rather than checking one 3×3 box and one digit, you can consider a single digit holistically, and determine if any of the 3×3 boxes are affected. At first you might use heuristics to determine where to search, but eventually you might start checking rules more systematically. If you’ve been stuck for a while, and finally make a new deduction, it’s good to check if that deduction directly leads to any new deductions, by checking how each rule would be affected by the new clue.
Applying guess and disprove
Even harder than determining where to apply your deductive rules, is when and where to apply guess and disprove.
“When” is very puzzle dependent. Some puzzles–and some puzzle creators–just have heavier reliance on guess and disprove. Some creators deliberately avoid it, which doesn’t necessarily mean that you should avoid it. For example, if you have a relatively weak set of deductive rules compared to the designer, you may have to rely on guess and disprove.
Generally, you want to create at most two branches with guess and disprove, and keep them as short as possible. If you can keep the branches entirely in your head, and disprove them in one step, all the better, it’s close to being a deductive rule. If you have more than two branches, it becomes hard to keep them in your head, and it’s hard to come up with a good way to annotate them. If you find yourself needing to split branches more than once, sometimes it is best to back up, and choose a different branching point to begin with.
Of course, if you’re solving a puzzle in MS Paint, as I have done many times, it’s easy enough to just copy paste the puzzle, and branch it that way. Back when I solved the “hardest” Sudoku puzzle by hand, I knew it would rely heavily on guess and disprove (that’s what it means to be hard!), so I printed out over a dozen copies of the puzzle and systematically organized my branches. When done right, it’s not really any harder than solving like 20 Sudokus in sequence.
Concluding remarks
Is any of that information useful for actually solving logic puzzles? Probably not, at least not directly. I think there isn’t any substitute for direct experience solving the puzzles. In terms of actually helpful advice, I think it might be useful to discuss, in the context of a particular type of logic puzzle, what deductive rules are available. I rarely see people talk about these outside of Sudoku, and the name “deductive rule” is my own invention. I see that SudokuWiki simply calls them “strategies“.
One thing that is clear, is that solving logic puzzles isn’t just a matter of applying a simple but tedious algorithm. There’s a fair bit of squishiness to the strategy, in formulating deductive rules, choosing where to apply them, and choosing when and where to use guess and disprove. This might not be obvious if you’re only familiar with one type of logic puzzle, but it’s important to understanding the logic puzzle genre at large.
Places to find logic puzzles
Nikoli – World famous periodical for logic puzzles.
USPC – Annual competition in the US (although it skipped 2020-2021).
The Art of Puzzles – Blog with contributors including some of the best-known logic puzzle designers.
Tatham’s Portable Puzzle Collection -Algorithmically generated puzzles, available on many platforms.
Puzzle Picnic – Website for creating and sharing logic puzzles.

Sudoku has it’s own set of what amounts to etiquette. To be considered proper a Sudoku puzzle should have a a single unique solution that can be derived using positive deductions that don’t depend on uniqueness. You should never need to use guess and disprove. Every solver I have watched solve a puzzle has used guess and disprove at some point though, it’s too easy when you have part of a puzzle down to a handful of possibilities that can easily be eliminated.
Using uniqueness depends on what you are doing. In Sudoku you will sometimes run across cases where it’s obvious that a particular set of solution could be rotated or mirrored and thus not unique before finding the deduction that eliminates the entire set. If you are speed solving then using uniqueness is fine. It’s often necessary to be competitive in a speed solving competition. When not going for a speed solution most people won’t take advantage of this.
Using math as part of a solution also divides Sudoku. One camp says no math in Sudoku while the other allows for puzzles that require math. My impression is that most Sudoku masters have no problem with math but a lot of casual solvers don’t want math in their logic puzzles.
I’ve often wondered if Sudoku would be much harder if you substituted other symbols for the numbers, like letters or something more abstract. Would it be an adjustment at all? How hard or easy would it be? I’ve sworn off sudoku because I used to be good at it, but on my most recent attempts I’ve run into puzzles that should have been easy and just ruined my night instead. If you’re not immediately good at something, it’s not worth bothering to try (/coachmcguirk).
–
I think Sudoku would be easier if it had colored symbols, instead of numbers. At least, it would to me. My habit with several of these puzzles is to represent numbers with colors, and solve them with colored pencil (or MS Paint’s fill bucket).
I got sent a ‘superdoku’ puzzle once, that was basically Sudoku, but 4x4x4x4 rather than 3x3x3x3. I found it significantly more difficult… not because the rules were any different, but because in normal Sudoku when you’re trying to figure out what might be in any row/column/box there can only be nine values total, and you’re generally never looking at four or more at a time. So remembring ‘this line has to contain these four values’ and then looking at the line to see if any of the spaces could only contain one of them is fine. A 4-scale Sudoku variant, suddenly there can be 16 characters per line, and you may have to remember eight as ‘these are the values in this line’… and suddenly that trips over the usual short term memory limit of holding six or seven things in your head at once. I’d often have to re-check exactly what was in any given line because trying to remember it often just exceeded my short-term memory limits.
And I have seen Sudoku books using things like baseball team logos instead of numbers.
It was almost ten years ago now that somebody managed to mathematically prove that the minimum solvable sudoku puzzle had 17 clues in it.
@2 Great American Satan: If it is just replacing the numbers with symbols on a normal puzzle it only makes a difference in your head.
If the replacement symbols are themselves used to include another component to the puzzle it can be much more complex. A typical puzzle like that might use the alphabet and add an additional constraints such as A+B+C < 12 or row one of box one contains no vowels and your forced to switch back and forth on what set of symbols you are thinking about to solve the puzzle.
my head is, of course, where the difference would be. we’re talking puzzles here. i’m human and not a brainlord. i’d been doing sudoku for a few years before it occurred to me that the use of numbers was arbitrary – not thinking that deep about it.