This is a repost from February, when LIGO reported its first observation of gravitational waves. This is relevant because last month LIGO reported its second observation, also resulting from inspiraling black holes.
Today, the Laser Interferometry Gravitational-Wave Observatory (LIGO) reported the first observation of gravitational waves. You can read about it in The New York Times (warning: autoplay), on Sean Carroll’s blog, or in comic form. I went straight to Physical Review Letters.
As an undergrad, I did some work on LIGO. Specifically, I was a data analyst looking for exactly the kinds of gravitational waves here observed. Anyway, I’m happy to play the role of your local expert, providing some context and answering any questions.
Gravitational waves were predicted a hundred years ago by Albert Einstein based on his theory of General Relativity. General Relativity argued that space-time bends in response to massive objects, and this distortion causes what we know as gravity. When a massive object moves, space around it needs to “update” in response to the motion, but this updating process is limited to the speed of light. Gravitational waves are basically what provide updated information about the distortion of space-time.
This is very similar to light, which provides updated information about the motion of electrical charges. However, light is an oscillation in the electromagnetic field. A gravitational wave is an oscillations in the very sense of time and length.
To measure gravitational waves, LIGO has a laser sent simultaneously down two perpendicular arms. A gravitational wave will make the light travel slightly faster along one arm than the other, and this can be precisely measured. The catch is that these arms are 4 km long, and the change in length is smaller than an atom!
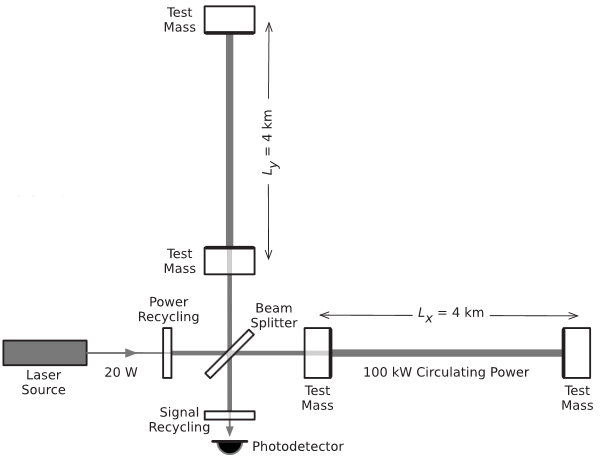
All images in this post were borrowed from the Physical Review Letters article.
Gravitational waves can be generated by all sorts of motion. But as sensitive as this instrument is, it is only sensitive to the greatest acceleration of the most massive objects. So we’re talking supernovas, fast-rotating pulsars, and colliding black holes. The particular event observed here is in that last category: colliding black holes.
What makes colliding black holes easy to detect is that we had decent predictions of what they should look like. The two black holes begin in orbit around each other. Because energy is radiated away through gravitational waves, they spiral towards each other, orbiting faster and faster, until they finally merge into a single black hole. After the merger, there is a “ring-down” in which the black hole’s event horizon settles back into a perfect sphere.
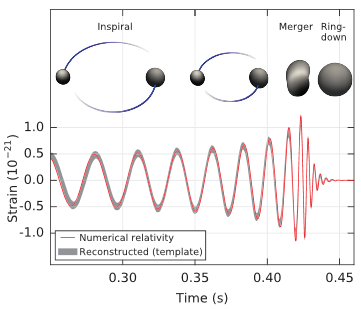
This matches closely the observation by LIGO:
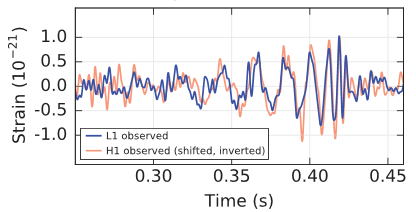
Now there are actually two identical observatories, one in Washington state, and one in Louisiana. The red line is from Washington, the blue from Louisiana. The data is shifted by 6.9 milliseconds, because the gravitational waves arrived at Louisiana first.
Let’s take note of the units. The vertical axis is strain. A strain of 10-21 corresponds to a change of 4 x 10-18 meters in the LIGO arms. The horizontal axis is time in seconds. One complete orbit corresponds to two cycles of oscillation. That means the black holes were orbiting more than 20 times per second!
Here are a few other big numbers in the paper. This event occurred on September 14th, 2015, but it occurred about a billion light years away. The two black holes were 29 and 36 times the mass of the sun. (That’s fairly big for a black hole, but they’re not the supermassive black holes you find at galaxy centers.) My favorite part: when they merged, they lost about 3 times the mass of the sun, because that energy was radiated out in the form of gravitational waves. Wow!
This shows not only that gravitational waves really exist, and that they really distort lengths, but also shows that they carry energy. Furthermore, it shows that black holes do in fact spiral into collisions with each other. I’m looking forward to estimates of the frequency of these events (and thus an estimate of the number of black holes), as well as the detection of gravitational waves from other kinds of events like supernovas.

I appreciate your offer to answer questions regarding gravitational waves. I am curious if gravitational waves can do physical damage near a black hole merger. For example, at a distance of 10 AU I calculate an average intensity of 3×10^22 watts / meter^2 for 3 solar masses of energy emitted within a period of 1 second. Certainly this would tear things like planets apart, right?
Thanks in advance for what I hope is a description of mind boggling destructive potential.
@Lenard,
I suspect that the gravitational waves would not destroy a person at 10 au, because the strain would be about 10^-9 or so. That’s a change of microns from your head to toe. Another physicist independently came to the same conclusion. A planet radius would change on the order of millimeters, but my guess is that the planet would stretch and compress so you wouldn’t even feel it.
I’d sooner worry about radiation. Some black holes have accretion disks, which radiate lots of x-rays as they fall into the black hole.
@Siggy (comment 2),
I get the impression gravitational waves are more ghostlike than neutrinos.
Lenard Lindstrom @1:
That is a lot of energy, but gravitational waves couple so feebly to matter that they hardly lose any of that energy when they interact with it. Of course, that’s also why they’re so hard to detect!
According to this, the attenuation length of a gravitational wave passing through Earth is on the order of 10^34 cm, or about 10^16 light years. So, not much energy transfer.