An empirical approach
When we hear two musical notes played together (either in succession, or simultaneously), we often characterize those notes as “dissonant” or “consonant”. But instead of having a sharp dichotomy between dissonance and consonance, it might be more useful to speak of a spectrum between the two. Then, the question before us is how to quantify the dissonance of any pair of notes.
12tone is a cool music theory channel, and he recently published a video discussing the solution thought up by the 18th century mathematician Leonhard Euler. I include the video below, but be warned that I’m going to trash Euler’s answer. I believe that any measure of musical dissonance must, at some point, refer to empirical observations of dissonance. Euler’s answer relies on mathematical supposition, and thus I would deride it as numerology.
When I say that a theory of dissonance must refer to empirical observation, I do not mean that we simply observe what people say is dissonant, and take that answer as truth. After all, what you consider dissonant might be different from what I consider dissonant. We could instead take a representative sample of the world population and measure the average opinion of dissonance, but this also has problems. On average, the world population has been strongly influenced by the western tradition of music. What we want is a measure of dissonance that transcends individual variation and cultural influence.
To do this, we generate theories of why we have this sensation of dissonance, and use empirical observations to select the best theory. Then we use the best theory to generate a prediction of what the average person would experience as dissonant in a hypothetical world where they were uninfluenced by musical culture. This has been done in a 19651 paper, “Tonal Consonance and Critical Bandwidth” by Plomp and Levelt, which I encountered when I did research on microtonal music.
Elegant, but wrong hypotheses
It is generally agreed that the most consonant musical intervals are the ones that have “nice” frequency ratios–that is, ratios between small integers like 1:2 or 2:3. So that set me to wondering if there was a “most dissonant” interval. I had a theory that the most dissonant interval would have a 1:1.618 ratio–that is, the golden ratio. Roughly speaking, the golden ratio is the irrational number that’s hardest to approximate with ratios of small integers.
It is an elegant hypothesis, but alas, it is not true. Plomp and Levelt disprove it. 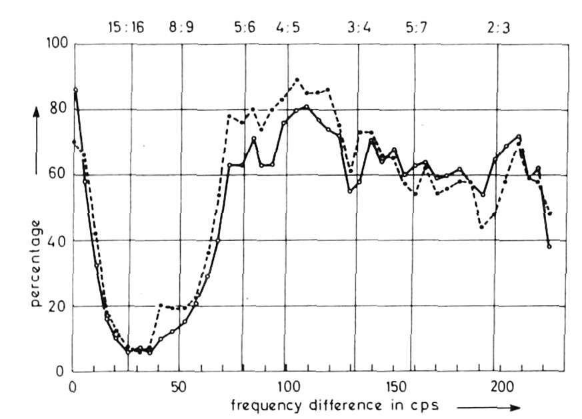
This is Figure 1 from Plomp & Levelt, but the data is sourced from an earlier work by someone else. They performed an experiment where they played a pair of simple tones, and asked subjects to judge which the tones were more consonant (solid line) and more pleasant (dashed line). As you can see, “pleasant” and “consonant” mean nearly the same thing among these experimental subjects.2 And the most dissonant interval is fairly small, near the 15:16 frequency ratio.3 Not the golden ratio.
I should mention that this experiment was performed on subjects without musical training. If we want to understand dissonance independent of cultural influences, then we had better use test subjects who aren’t deliberately trained in those cultural traditions. But this is something that most investigators before the 20th century didn’t understand. They were only interested in experiments on musically trained subjects.
As a result, they missed or ignored a significant fact: above about a 5:6 ratio, most intervals sound about equally consonant to untrained ears, whether they consist of “nice” frequency ratios or not. This conflicts with the traditional western understanding, and also with Euler’s theory. What gives?
A matter of timbre
Earlier, I referred to “simple tones”, and I’m going to have to explain that part. A simple tone is a sound produced by a perfect sine wave. Most musical notes, such as the notes played by a piano, are “complex tones” have many sine waves (harmonics) overlaid on top of each other. The frequency of these harmonics are in a 1:2:3:4:5:etc. ratio. Wikipedia has a nice demonstration of how simple tones can be overlaid to create a complex tone (caution: may be loud). The particular way that sine waves get overlaid is one aspect of the “timbre” of a note (pronounced “tamber”).
So what happens when we perform the same experiment using complex tones instead of simple tones? That is the subject of Figure 2.
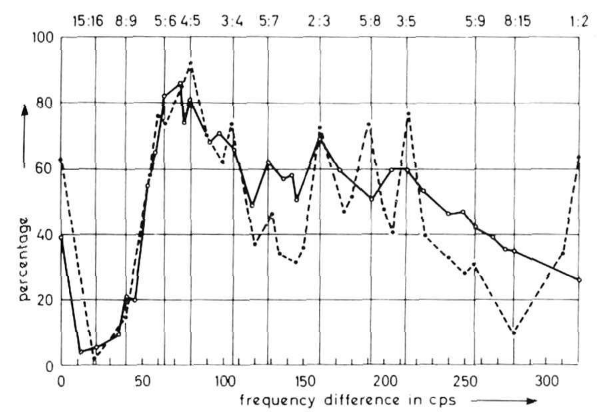
Figure 2 is based on another earlier study, which played pairs of tones for untrained subjects and asked them to judge pleasantness. (The curve looks more compressed compared to Figure 1 but that’s just because of the horizontal scale.) The solid curve shows simple tones, and the dashed curve shows complex tones. So when we switch from simple tones to complex tones, there appear peaks in pleasantness that correspond to “nice” ratios between integers.
Well isn’t that interesting? Using simple tones, untrained listeners do not much care whether tones have nice frequency ratios. However, when we use complex tones, nice frequency ratios are preferred. Plomp & Levelt argue that this supports a theory of dissonance that they credit to Hermann von Helmholtz. Fundamentally, the sensation of dissonance comes from tones that are close together in frequency. This includes not just the fundamental tones, but also the higher harmonic tones. So if we have two complex tones, the higher harmonics create dissonance, unless the two complex tones happen to have a nice frequency ratio with one another.
I will gloss over the part where Plomp & Levelt discuss other theories of dissonance, and why they fail to account for this data. Let’s just say that Euler didn’t have much of a theory, believing that the “unconsciously counting soul” simply likes concurrent vibrations.
Dissonance and the human ear
Plomp & Levelt perform additional experiments, mainly trying to understand how close simple tones must be in order to produce this sensation of dissonance. Earlier I said 15:16 was the most dissonant interval, but that’s not always true. In fact, it doesn’t just depend on the frequency ratio, but also the absolute frequency. In the lower frequency range, the range of dissonant intervals is larger.4 In the higher frequency range, the range of dissonant intervals is narrower.
They make a connection between the range of dissonance, and “critical bandwidth”. Critical bandwidth is an idea that comes from the study of human hearing. Basically, it’s how close two frequencies can be before one tone interferes with the perception of the other. Apparently when the distance between two tones is about 25% of the critical bandwidth, it produces this sensation of dissonance. When the distance is much greater than or much less than 25%, the dissonance is diminished.
Using this knowledge, Plomp & Levelt are ready to make predictions. The following figure shows the prediction of consonance between two complex tones, as a function of distance between the tones. These complex tones include only 6 harmonics, so the function lacks peaks corresponding to, e.g. the ratio 5:7. In the case of realistic musical instruments, the landscape of dissonance would have more of a fractal structure.
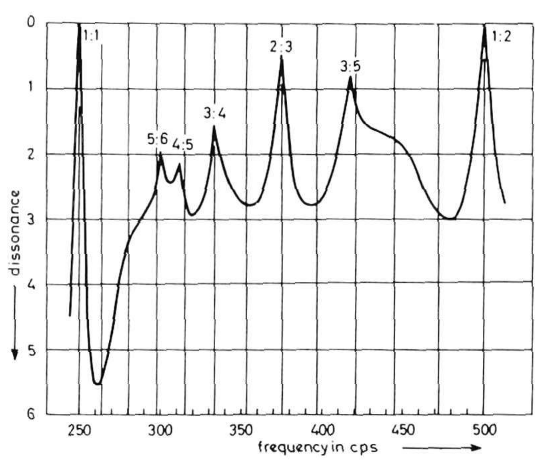
The takeaway is that musical dissonance does not just depend on mathematical frequency ratios, as Euler believed. It depends on the timbre of the note, the absolute frequency of the note, and the properties of the human ear. Last but not least, it depends on your culture and musical training.
1. The skeptical reader may ask whether a paper from 1965 still holds up today. I am not an expert in the field so it is hard to say. However, I found Plomp & Levelt because it was discussed approvingly in the introduction to a 2000 paper by Marc Leman. This suggests to me that Plomp & Levelt has held up fairly well. However, it seems that in modern scholarship, the term “roughness” is preferred over “dissonance”. I stick with the word “dissonance” to be consistent with the paper under discussion. (return)
2. The subjects of this experiment were not musically trained. Among musically trained people, there is more of a distinction between “dissonant” and “unpleasant”. This suggests that “dissonant” is not the same as “unpleasant”, but rather a distinctive quality of sound that untrained listeners (in western culture) tend to find less pleasant. (return)
3. For those who are wondering, the 15:16 ratio is close to the minor second interval. 8:9 is close to the major second, 5:6 is close to the minor third, 4:5 is close to the major third, 3:4 is close to the perfect fourth, 5:7 is close to the tritone, 2:3 is close to the perfect fifth, 5:8 is close to the minor sixth, and 3:5 is close to the major sixth. I say “nearly” because in modern western music all these intervals actually have irrational ratios. The funny thing is that because of my musical training, intervals with rational ratios sound slightly dissonant to me, because they’re out of tune relative to western tuning. (return)
4. This echoes conventional wisdom among musicians, that small intervals sound worse in the low registers. (return)

Basically, tonal theories (i.e., the “tradition” for most of the last few centuries) aren’t complete theories of musical harmony. They presuppose that certain scales and sonorities will be involved. (And that they have a tonal “function,” which is a bit of a mysterious term, but it’s the one we use.) Categorizing different chords/intervals/etc. according to their tonal function usually works pretty well, when describing how one chord should progress (or resolve) to another, in music which fits in this framework. Even then, it’s rather problematic, but it’s definitely not able to cope with anything beyond that.
People typically think that once they’ve got a handle on that stuff, they have thus “learned music theory” or at least the basics of what it says about harmony. But that is incorrect. They learned a theory that was developed mostly during the Renaissance and Baroque periods to try to make sense of what they heard then, along with some input from older theories of counterpoint that remained relevant. It’s sort of like studying old alchemy texts and thinking that you have a decent grasp of modern chemistry.
Anyway, going back to the issue with consonance and dissonance…. People have somewhat differing ideas about them, as you point out. But it is basically just the smaller intervals that are (more or less always) considered dissonant. It has nothing to do with the rational numbers, as Pythagoreans and Platonists used to think.
When I said dissonant intervals are smaller, that also means their inversions. The “inverse” is the additive inverse modulo 12, when there are 12 equal divisions of the octave. For example, 1+11 = 0 (mod 12). The point here is that the interval 11 (major seventh) is not small like 1 (minor second) is, but it is a small distance away from being an octave. Octaves are consonant, and they are even equivalent (although not identical) in the sense of being the same pitch class. To some extent, especially with untrained listeners, people won’t notice as easily that there is dissonance between a large interval like 11 and the nearby octave. That octave (call it “12”) is present in the harmonic series of the lower pitch (“0”), but it generally won’t be as loud, making it less noticeable (at least to some). So, for reasons like that, [0E] is not quite the same as [01], but that’s the basic idea.
You might be misinterpreting here. Just to clear up any potential confusion…. Like I said above, the “niceness” of it doesn’t need to be about rational numbers with very small integers. Some of those happen to be consonant, like 1:2, 2:3, 3:4, 4:5, 5:6 (and their inversions). But that’s just coincidence, and it is only a (beneficial I suppose?) side effect that it will not make baby Pythagoras cry about the number being irrational. The issue is that both fundamentals won’t create noticeable “conflicts” with each other in the lower parts of their respective harmonic series, since those pitches are also present in ordinary circumstances (as we know from physics). People can’t really tell that some proportion of frequencies is exactly 2:3 or what have you. It depends on the exact nature of the experiment, but generally their pitch discrimination is actually pretty lousy. So, any arbitrary irrational ratio of frequencies will suffice, if it is close enough to being some such interval with the property that the overtones don’t grind up against one another “too much” for most people to know or care that it is happening.
There is another set of effects to talk about — not just the big dip around the small intervals and their inverses, but also the fluctuations in the higher parts of those curves. I think a lot of that just has to do with familiarity. Some intervals are heard a lot and are given a certain status in tonal music, while others are much less familiar. People who’ve listened to music like that their whole lives won’t necessarily forget that sort of thing when they have to be in an experiment.
@CR #1,
Yeah, I agree with what you’re saying. I wish this whole thing would be taught as a standard part of music theory, because I always had the impression that we just didn’t know why certain ratios were more consonant than others.
You are right that complex tones don’t need to make nice ratios in order to avoid dissonance, and I was speaking imprecisely. There’s a window around each nice ratio that still sounds consonant, and there may be other intervals where as it happens there’s just no clashing among the loudest harmonics.
I also think that in some instruments that only have odd harmonics, maybe there are even more consonant ratios. I’m tempted to try programming such sounds, to hear what it sounds like.
Well, that pretty much boils down to a question of whether you like certain timbres or combinations of timbres. Do clarinets sound good to you? Do you like them playing with some combination of other instruments/voices, especially when they are playing specific sets of notes? If not, do you like something else? And so forth.
You could call that “consonance” if you wanted to. But then, doesn’t the context of the sound still matter? I mean, you can hear one thing and say it’s terrible, but you might change your mind about it in the right circumstances, if for example it’s set up in a particular way or leads somewhere interesting. Or, suppose you have the idea to compare it to your experience of a major triad on the one hand, or on the other to some dense cluster of what you can only describe as irritating noise. It might sound relatively consonant compared to the latter. Or it still might not sound so great even by comparison to that, but in some other context it would. It’s very easy to think of cases where some usually-pleasant sound is just plain awful because of what else is happening in the music (before, after, or at the same time).
To be a bit more concrete about it…. People used to think the tritone was the “diabolus,” but I have no doubt that you like listening to them on a very regular basis. Indeed, they’re pretty much unavoidable in tonal music, not to mention other kinds of music. Part of it is they’re not used in the same ways they were centuries ago. If you don’t really know what to do with them or how to listen to them, as people didn’t, then it’s not hard to imagine that may be a problem for you. But that can certainly change if learn some new ways to think about harmony (or are simply exposed to it as a listener). The point is that it’s just getting started on the wrong foot to think of it as if there were some fixed property of a sound which you can understand in isolation, like a statue or an equation or I don’t know what, without thinking about how it relates to other sounds in the music (or in your memory, etc.) or without thinking about all of the things you’re bringing to the table whenever you listen to it.
In any case, timbre does matter a great deal. Real life is obviously more complicated than the simplistic version of the story that is usually peddled. It’s easier to talk about it as if there’s just one frequency (the fundamental) — a note gets a number, and then you say there’s a proportion between that and some other number that is meant to describe another note. Seems like a nice idea, but the only problem is that the real world is not nice (or maybe it’s even nicer than your idea).
Anyway, something like a 1D number line is simply inadequate for representing everything that plays a role in your listening experience. For that matter, we wouldn’t even have to bring up timbre, just plain old musical sets. They were given numbers (by Forte back in the 60s or 70s, according to some very arbitrary rules he dreamed up), but it’s just sort of meaningless to list them “in order.” You might be interested in Dimitri Tymoczko’s (and others’) work on geometrical music theories. He did some popularizing a few years back, which I think is a bit sketchy at times, but there is a more serious side to it. For example, the space of the 3-note set-classes is shaped like a cone. In those spaces, they do go from more densely-packed clusters on one end to more evenly distributed on the other (near the point of the cone in the 3-note case), but they form these big, complicated and rather interesting structures, rather than something simple like a line or a list of objects.
@CR #3,
There’s no doubt that the context matters, I was just curious what it would sound like. Not, “does it sound good?” (I don’t think dissonance sounds bad anyways) but rather, “does it sound different?” Would a major 7th interval sound significantly more consonant on clarinet vs other instruments? Or would my classically trained brain hear it about the same way?
I seem to recall that Sevish programs music with inharmonic overtones (mentioned here), which he claims leads to a smoother sound. I’m not sure how well I notice it though.
I don’t know. Probably not very significant, since the odd partials still rub up against each other.
A combination like that will sound different from other instruments, of course. Generally, I would not want to put something like that in terms of consonance versus dissonance. I rarely think that way in the first place, so maybe it’s just me. Often, I’ll use somewhat more descriptive language … metaphors like cool, warm, hollow, full, rich, and so forth. Or maybe something is a little spicy or pungent or whatever.
I tend to associate “consonance” and “dissonance” with resolving a chord in tonality, such as a cadence with a (more dissonant) dominant triad resolving to a (more consonant) tonic triad. Notice that these are same types of chords (both major triads), so what people mean by it isn’t about the structure of that particular group of notes having a particular property. But the dominant contains the leading tone in that particular key which people think “pulls” toward the tonic note. Because you were prepared for it, you hear that pulling as if it were an intrinsic feature of the dominant triad (although it isn’t), and the whole bit of music doesn’t seem finished until the tonic.
Or for another kind of example, there may be a note that “anticipates” the next harmony, which sounds dissonant at first but consonant once the other parts reach the second chord. In the dominant-tonic example, the anticipation could be the root or third of the tonic triad (the fifth is already in both, so it’s not a very helpful example).
Anyway, if stuff like that isn’t happening, or if it’s not even tonal music let’s say, then those terms aren’t especially useful. But I’d still want to know something about what I’m hearing, so other concepts might still help.
Well, he can claim that if he wants, but it sets off my bullshit detector. Too much woo out there about the golden ratio already. And I’m not really a fan of the way certain composers (especially in microtonal music) start with some random bit of math and treat it as if that does some kind of magic. Very generally, if your theory involves all sorts of complicated crap that has no impact on what real people can actually hear, it’s a bad theory.
I have a good ear, much better than most, since I write/arrange all the time and have to use it constantly. But I’m sure I can’t tell the difference between 1.618 and the number phi, if that’s applied to something musical like a scale or whatever (and since we’re being realistic, computers also need to use approximations at some point, meaning we’d have to be very lucky and hope it just happens by accident). So it doesn’t really matter which number you call it, because they go into the same bucket for me. If you’re writing music for Superman, and if he can tell the difference, then I accept that he puts them in different buckets and that your theory may be able to account for that, when discussing Superman’s listening experience (but not anybody else’s). Otherwise, things like that just won’t be relevant.
@CR #5,
I checked and yes, the 5th harmonic of one note rubs against the 9th of the other, fwiw.
I don’t think Sevish is in that set. Anyway, it seems like electronically removing dissonant harmonics would have a real impact on what people hear–that’s basically what’s going on in Fig. 2 of the OP.
I have been reading Helmholtz’s papers and find it very interesting. I think overtones beating against each other definitely has a lot to do with dissonance of intervals for humans. Personally I still think a P5 sounds more consonant than a Maj7 with pure sine waves despite Helmholtz research. I wonder if it is because I am conditioned to hear P5, P4, M3, M6 as the most consonant intervals? I think beating as well as simple ratios have to do with consonance of sine waves or any other wave.
Here is a good article that points out the cons of Helmholtz’s work: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2607353/#idm139704480569216title
Some of the research shown in this paper shows consonance spikes around p5 and octave with sine waves with no harmonic present. The studies are suggesting here that overtones don’t need to be present to hear consonance at simple ratios.
Here is the article that is referenced in the paper: https://link.springer.com/content/pdf/10.3758/BF03200773.pdf
@Mirage,
I’m looking at the Lots & Stone paper. When they refer to Plompt and Levelt, they agree that the main effect seems to be the “roughness” arising from two nearby frequencies, but they also highlight the other peaks and valleys, such as on the right side of Figure 1.
I agree that there appear to be lots of peaks and valleys but, I’m not so sure of the interpretation. It seems consistent with the hypothesis that perhaps some of the listeners have a bit of passive ear training, based on a musical environment that developed around complex tones, not simple tones.
I mean, I would not be surprised if there were some additional neurological effect like the one that Lots & Stone describe, that makes the 3:2 ratio more consonant even to untrained listeners. I’m just not strongly convinced that the data calls for such an explanation, given the obvious confounding factors. I’ll believe it when there’s evidence that untrained listeners prefer the 5:4 ratio over a major third, or the 7:4 ratio over a minor seventh in pure tones.
I also can’t say I really understand Lots and Stone’s explanation. Why would neurons fire off at a frequency that is much slower, and yet proportional to the frequency of the tone? You need a pretty unusual physical system to get such behavior.
@Siggy Yes I still think what really causes consonance and dissonance is still up in the air. I still tend to want to lean to Pythagoras idea over “cleaner” ratios sounding more consonant. Though, with complex tones I think the beating of overtones help strengthen the dissonance of “dirty” ratio intervals. It will be interesting to see newer research that gets released hopefully!
Here is another interesting video that discusses Helmholtz’s theory: https://www.coursera.org/lecture/music-as-biology/a-physical-explanation-of-consonance-bBGS1
The main argument the Duke professor presents is when 2 sine waves at different frequencies are played in separate ears there will be no beating present, yet studies are still showing dissonance.
@Siggy Also to add onto the brain eeg data here is the article the paper is referring to if you have not looked: http://www.brainmusic.org/EducationalActivities/Itoh_consonance2003.pdf
@Mirage,
It’s pretty interesting that the roughness sensation is present even when each pitch is in a different ear. Frustratingly, I was not able to program an example of this, nor find any example online.
@Siggy I just made a quick midi of 2 sine waves playing in different ears. One sine wave hold C in the left ear while the other sine wave plays in this order: minor 2nd, Major 3rd, Tritone, Perfect 5th, Major 7th, Octave in equal temp. https://soundcloud.com/mirage-productions/sine-waves-separated-by-ear-in-equal-temp/s-9ZX8u
@Mirage #12,
Thanks for that. Apparently my computer’s speakers just don’t play stereo properly (that’s why I was having difficulty programming it), but I was able to hear it on a different device. Very fascinating, and contrary to how I understood hearing! I believed that the sensation of a beating frequency arose directly from alternating constructive and destructive interference. And yet, I would not expect that two sounds played for separate ears could ever interfere destructively. So this implies that the sensation of beating frequency has a different origin than I thought.
I would be interested to run more tests, to see if the sensation of a beating frequency changes for low enough frequencies. If the beating frequency is only 1 Hz, I would expect mono and stereo to sound quite different! I better troubleshoot my speaker problem.
I want to expand on a point from the end of my comment #3. Maybe it sounds radical at first, but I think the whole idea of a consonance-dissonance spectrum is confused. Two-note sets could be ordered that way, because they form a 1-dimensional space (topologically, a circle). There are still other issues (see below), but at least they have that much going for them.
However, the configuration spaces of sets with more than two pitch-classes simply aren’t like that, so the concept of putting them in a particular order (from “more consonant” to “less consonant”) seems to break down entirely.
You’d be asking questions like “is 90 degrees east closer to the north pole than 90 degrees west, or vice versa?” It’s a loaded question, of course, and you can very well respond by saying it’s neither. But if you persist, you can say they’re at the same latitude, so to speak, meaning it’s a tie. Some may not be happy with that response (who knows why), but let’s suppose there can be a tie. No complaints from me.
But then you run into another sort of problem, which is that by construction, the tightly-clustered sets are adjacent to multisets. These sets contain multiple copies of a PC — that is, they have unisons/octaves, which are normally considered very consonant and not in the same neighborhood as the most dissonant harmonies. In any case, zero is the smallest positive number, so there is nowhere else for it to go, if we’re applying these ideas consistently. And if we said at this point that inconsistency is okay, and we’ll just juggle things around until we get what we thought we wanted, then I guess I just don’t understand what we’re supposed to be doing with this theory anymore. And I think it seems very fishy.
Then there are various things which people say about microtonal harmonies, that introduces a whole other level of complexity. (Some people think they’re all bad, others think some of them are the only truly good ones, and practically every other thing gets said by at least someone out there.) I’m not even sure where to begin with that, and this is becoming too long already. But for the sake of completeness, there should be a way to make sense of those too.
What I would say is that people have some sort of vague idea of “consonance,” which generally works in communication, in the sense that this word gets used in more or less the same ways by most people (depending on learning, culture, etc.) so they can try to understand one another. Of course you can test how people use words, and you might even come up with something interesting. But this ordinary usage doesn’t need to be applied systematically to all possible harmonies. It just wasn’t designed to handle anything like that (similar to other folk psychology theories, ordinary intuitions about physics, or what have you), and we shouldn’t be surprised if something like that turns out to be inadequate.
@CR #14,
I don’t follow. Even with two-note combinations, there have to be “ties”, so I don’t see what special problem is posed by larger combinations of notes.
I don’t think “consonance” is an adequate theory of what’s going on though. I think a more complete theory would identify several latent variables, including a few dimensions of roughness, as well as factors unrelated to roughness. Consonance would be a function of all those latent variables, and would be mediated by individual and cultural preferences.
Siggy, I don’t see why a tie would be logically necessary for intervals (two notes). There is inversional symmetry, meaning certain pairs of intervals must be equivalent in that respect, but that doesn’t entail that a person experiences them as equivalent in terms of their degree of consonance/dissonance. When I hear a major third and a minor sixth, for example, it’s far from obvious how I could establish that I hear them as equally consonant, despite knowing perfectly well that they’re inverses. So perhaps I should say one interval is more consonant than the other after all; it’s not clear why it would be a forced choice. They’re not identical, and for all I know, that may be an appropriate way to distinguish them.
This symmetry by itself ought to say perfect fourths and fifths are tied, but many would argue against that, particularly when their thinking is based on the harmonic series (in which fifths are obviously more prominent). They’re just coming at it from a different perspective and getting different conclusions. I don’t know how to adjudicate that, other than to say they couldn’t both be right but they could both be wrong.
Anyway, the main point was that I can imagine a mapping of some kind from the intervals to a number line, even if that’s not how you’d do it, but that simply couldn’t work with larger sets. If you’re happy with ties, then like I said that wouldn’t be a problem for me (but not everybody). Generally, I guess the more critical points boil down to whether it’s consistent and whether there is continuity, along with lots of questions about how the whole thing is supposed to work in detail. At least we can agree that it’s inadequate, so that’s something … but the criticism is directed at people who think otherwise (or seem to think so).
I was wondering what yall thought about the Maj7 interval as pure sine waves. Helmholtz claims that maj7 should be just as consonant as an octave and p5, though I personally disagree. I wonder if I am conditioned or if others experience this as well. I hear maj7 having a little bit of a “gritty” unstable sound even as sine waves.
Here is a good video that plays all the intervals of the first octave in just intonation: https://youtu.be/nSo6WlGk5jw?t=81
@Mirage #17,
I feel like the “dissonance” of m2 and M2 intervals is qualitatively different from the “dissonance” of larger intervals (in pure tones). m2 and M2 have noticeable beating frequencies, while larger “dissonant” intervals just give me a sense of wanting to resolve to a different chord. So what I hear in an M7 interval, is something that wants to resolve to the tonic.
@Siggy yeah I agree that the m2 and M2 sound more aggressive on the ears vs the larger intervals. m9 sounds more stable than m2. I just made a loop that shows octave vs M7 in equal temp. I noticed when I dropped the intervals down an octave the M7 sounds more dissonance. I am not sure why this is. To me the lower octave makes the Maj7 have more of a “beating” effect you get with m2.
https://soundcloud.com/mirage-productions/octave-vs-m7-sine-waves-in-equal-temp/s-v224p
I just don’t hear a beating effect in the M7 intervals.
@Siggy Interesting, not even the lower octave? It sounds rough to me, especially at the lower octave.
Pure tones that are M7 apart should have no human-hearable beating, so I guess I’m not sure what you’re calling roughness. Does the roughness have a frequency to it?
@Siggy If you listen to the lower octave you can hear it sound like the interval is “shaky”. I have asked others if they can Identify the shakiness of the interval and have agreed. The higher octave is a lot harder to identify.
Whatever shakiness I hear is also present in the octave interval.
I asked my partner which ones he thought were dissonant, and he picked out the octave in the high register, LOL.
@Siggy I believe my left side of my headphone is possibly adding an octave overtone. Is it possible for my headphones to be adding an overtone without it being present? On the right side I don’t heat the beating, though on the left I hear an ever so slight beating. I think my left is adding an octave overtone causing the minor 2nd beating effect possibly.
I was doing some research and believe what I am referring to is secondary beats.
https://ccrma.stanford.edu/~malcolm/correlograms/text/62%20Primary%20And%20Secondary%20Beats.html
Though I don’t think it has a great deal to do with dissonance perception. I think it more has to do with beating and not roughness/dissonance. I am starting to be more and more convinced with Helmholtz theory than any other for consonance and dissonance.