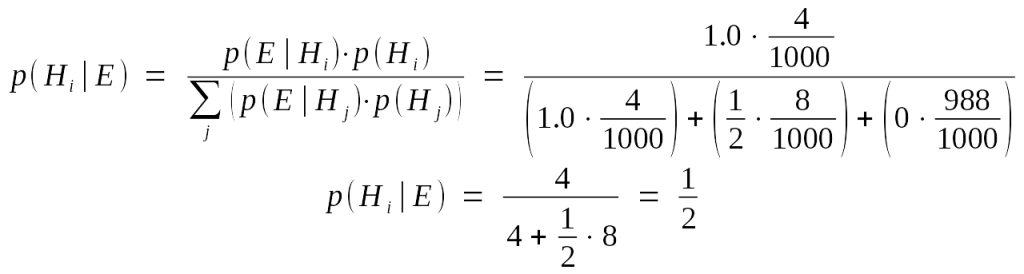This one demanded to be shared ASAP. Here’s what you need to know:
- Identical or monozygotic twins occur in roughly four births per 1,000.
- Fraternal or dizygotic twins occur in roughly eight births per 1,000.
- Elvis Prestley had a twin brother, Jesse Garon Presley, that was stillborn.
For simplicity’s sake, we’ll assume sex is binary and split 50/50, despite the existence of intersex fraternal twins. What are the odds of Elvis being an identical twin? The answer’s below the fold.
As always, we start off with Bayes’ Theorem.
 Normally I’d immediately switch to the Odds Ratio form, but I think this problem works best with Bayes Classic.
Normally I’d immediately switch to the Odds Ratio form, but I think this problem works best with Bayes Classic.
We only have three hypotheses here: Elvis was an identical twin (I’ll call that Hi), Elvis was a fraternal twin (Hf), and Elvis was something else (He). The normalizing constant on the bottom is just the sum of these three hypotheses, multiplied by their respective priors. Those priors are
| Hi | 4 / 1000 |
| Hf | 8 / 1000 |
| He | 988 / 1000 |
Now, to figure out the likelihood of the evidence (E), given each hypothesis. He is the easiest; since the evidence states Elvis was a twin, the likelihood of him not being a twin is zero. Hi is almost as easy; the odds of seeing a twin brother, given Elvis was an identical twin, are 100%.
But what are the odds of seeing a twin brother, given Elvis was a fraternal twin?
| Male | Female | <- Elvis | |
| Male | legit | impossible | |
| Female | legit | impossible | |
| ^ Twin |
In our simplified universe the genders of twins are uncorrelated. We already know Elvis identifies as male, so we can discard half the potential outcomes as impossible. Hf is compatible with both a potential twin brother for Elvis as well as a twin sister. It isn’t as specific as Hi and so dilutes its certainty over potential outcomes, making any specific outcome less likely. How unlikely? Well, we have two legit outcomes under Hf, and since each is equally likely we assign each equal probability and normalize so the sum of both is still 1. So the likelihood of a twin brother, given Hf, is 1/2 or 50%.
Now it’s just a matter of plugging values into the math.
The news that Elvis had a twin brother wound up boosting the odds of him being an identical twin. That’s counter-intuitive to me, and I think the reason is that we tend to ignore contrary possible outcomes. We knew the twin was a boy, so we didn’t include Hf‘s prediction of a twin sister in our calculations. Without that, we only see one possibility for the likelihood and thus mistakenly mark it as 100% instead of 50%.
If you’d like a bit of homework, try relaxing some of the assumptions. What if we drop the binary, or use actual twin gender prevalences? How does the math change then?
This is much more than a cute parlor trick. Consider: how likely is an unexplained creaking, given the existence of the supernatural? It’s entirely possible a spirit would try to grab your attention by flexing the floorboards, but it’s also possible they would knock on a door, rattle a window, draw notes in the air, whisper in one ear, or do pretty much anything else. The likelihood is thus vanishingly small.
In contrast, how likely is that creaking given the hypothesis that houses creak with temperature changes? Pretty much a certainty. So if you pit these two hypotheses against each other, the naturalistic one is going to come out on top, even if the priors against it are severe.
If your hypothesis explains everything, it shouldn’t be believed. Now, pray tell, what does “a god did it” explain?