Below is a greatly simplified chart of the history of mathematics. The interesting bit is the black bar on the time line, which indicates where (optimistically) high school math stops. With calculus? I got pre-calc/trigonometry in high school, most of our incoming students haven’t had calculus yet, so it’s a little bit off.
Wait. I’ve had a fair bit of statistics…that’s early 20th century! What a relief, I won’t have to worry the ridiculous over-the-knee boots and pelisse when my classes drift into a little mathematics.

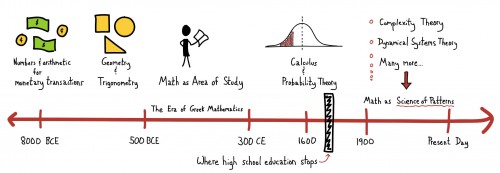

High school math pretty much ends with AP Calculus, at least in my district. The larger high school in our area has AP statistics. The good news is good students can go to the local community college and get classes up through linear algebra and multivariate calc. One of my former students finished all the math offered here before he graduated (at 16!) and went to UC Berkeley.
I’m actually disappointed about the stuff they don’t cover. I’m surprised they don’t teach a very light introduction to modular arithmetic, computability theory and complexity theory. It’s super accessible. I explained the halting problem to a 12 year old. In large part I think this has to do with how subjects are organized in the US. It might be that a trig course or an algebra course is too compartmentalized to lightly touch on all the areas the should. Most other countries don’t organize things quite this way.
This has long been a favorite ploy of mine, especially in calculus classes (where students tend to be more receptive to this kind of thing): “Okay, everybody! We’ve gone roaring into the 17th century now. Our math is getting really advanced!”
Sometimes I’m fortunate enough to pique their curiosity about what 21st century mathematics is. If only I knew …!
@Sugarfrosted: Computability and complexity theory are both much more specialized, so there’s good reason not to teach them in math – they go a lot more in computer science (even if there’s a lot of overlap). I will admit, though, that as a CS theoretician, I’m annoyed that nobody even knows CS theory exists in high school. Heck, very few people know CS theory exists in college – the theory course at my undergrad required junior year (though it was often waived to let sophmores in, because there was no actual reason for it to be restricted) and the majority of our majors only had the one theory course.
The fact that our high school math ends so early sheds some interesting light on the fact that we don’t cover any discrete higher math in high school, too – the foundations of graph theory weren’t until the mid 1700s with the Bridges of Konigsberg, set theory came in the late 1800s, while we do cover some number theory (factorization, divisibility, etc) in high school, and that goes back much further. It makes the idea that high school math stops after the 1600s… weirdly accurate.
Sorry, PZ, but Statistics dates way before the 20th Century. All the basic ideas and theorems and so forth date back to him — it’s why Pascal’s Triangle is more famous than the Binomial Theorem, even though they are just two ways of calculating the same thing used in statistics. Admittedly the application of calculus to statistical questions didn’t come about until later — primarily because calculus hadn’t been invented yet — but the field as an object of study goes back a long way.
I didn’t take pre-calc, trig, or statistics in high school. Weren’t required to graduate. Even with the PSEO shenanigans.
IIRC, I took algebra, geometry, trig, and pre-cal in high school. Algebra was the only course I performed decently in. I did poorly at geometry. I think I escaped with a D-. I did a little better at Trig and pre-cal. I’ve never been good at much above algebra. Math just isn’t my strong suit by any stretch of the imagination.
A few years ago, I visited my parents in southern Florida. One day when I woke up from a nap I saw my mother intensely engaged in some kind of work. I walked over and peered over her shoulder and could tell it was some type of mathematics. I asked her about it and roughly 10 seconds later I had to ask her to stop because I didn’t understand a thing she was telling me. See, my mom *loves* math and she’s as good at math as I am bad. She loves statistics, she loves calculus, and other higher end areas of math. And that work she was doing? She was doing it for fun.
That”s not a US thing.
From what I remember, the high school program in France ends at the same period for mathematics.
Physics program ends at the start of the 20th century or even before (I learned thermodynamics at the start of the equivalent of college). Relativity and quantum physics are definitely not part of the high school program)
Biology on the other hand included a basic understanding of genetics. My parents never heard of chromosomes and DNA before college.
Maybe all of that will change if we start to take vacation on other solar systems (for all of you going to alpha centauri this summer, see you in 20 years) but I have some doubts :-)
We were doing calculus in school in year 10 – if not earlier.
As for the date – well Archimedes was doing it in the 4th century BC – not quite as efficiently as in its later rediscovery but given the tools at the time…
Teaching of linguistic concepts stops somewhere around 2500 years ago , so I think maths is looking pretty good. https://en.wikipedia.org/wiki/Pāṇini
I remember doing a bit of graph theory in maths class, but I suspect that was only because I went to England for a year and had to take some kind of advanced Sixth Form course there for complicated reasons.
Seriously though, we get students now who can’t identify a Dative in a German sentence, or tell me what a subordinate clause is. What Do They Teach Them In School These Days.
@9 madtom1999. Calculus has an odd history of being nearly discovered or being discovered and lost again. One other example of this was the research group in Oxford, “The Oxford Calculators, that discovered certain aspects of Kinematics and probably would have discovered calculus in the 13. century, except the majority of the research group died from the plague. (Ironically, this nearly happened to Newton as well.)
@4 I feel that it’s the type of thing that you could prove the halting problem and explain what complexity is, just as part of making people know about it. Kind of how they teach Shakespeare in English, though reading Shakespeare doesn’t really make you better at reading and literary analyse. (Also it probably should be covered in something about computing. I just tend to view it as part of math, because of my biases, i.e., I’m a grad student who studies computability.)
In my pre-highschool education I was irritated by the number of years of redundant arithmetic. After being taught how to do arithmetic with single digit numbers and how to expand the process to two digits, I understood how to handle any number of digits. Yet, I was still stuck in math classes working with larger and larger numbers but not actually doing anything new. Algebra was finally available in 8th grade, if you had special permission. I took 4 years of math in high school, ending with AP Calculus.
I eventually went on to an engineering degree at college, with calculus just the entry level math class. Many math classes later, I feel like I’ve had enough math classes to really realize that I’m still swimming in the shallow end of the pool and that it can get far deeper.
It was possible to take Calculus at the high schools I went to but only if you were in an advanced math track which meant you took geometry in grade 9 instead of the usual algebra. At my middle school, even the advanced math track only placed you in algebra for grade 9. At the school I graduated from, they’d let you take geometry and trig in the same year which meant you could get Calculus as a senior but it wasn’t something they advertised.
I would have taken calculus in high school… I think. High school is the one with the first legitimately important set of exams, right? I’m never sure how American school words map to the UK system.
I got dropped down into the second set for maths after my first year, because I didn’t do enough homework, and ended up being pushed back up into the first set for the last few months leading up to the exams, so I ended up getting the back end of calculus and not really having a clue what was going on. I still did well in the exams, though. Fortunately I picked enough up in my foundation year at uni, and there are sites like coursera.org now that allow you to take calculus courses for free, so we’re not doomed by what schools decide to teach us or how they shuffle us around anymore.
The level at which maths stop also depends on the character of the school. I went to a small rural high school where maths topped out at Algebra II. Pre-algebra was not available until 9th grade and there was no advanced track. Few graduates went beyond community college and fewer obtained 4 year degrees. Advanced maths require incentive, for which there was none because as I wrote, college was not assumed to be a goal, and competent advance math teachers, which such schools do not attract.
Don’t you have vectors in U.S. high school math. AFAIK, they’re from 19th century.
I was part of a (large) group of mathematicians (professors, graduate students, and some university seniors and juniors, including me and my roommate Hal Abelson—we both went on to get our Ph.D.s in mathematics at MIT, but he converted into a computer scientist and is still there…) who wrote a more-or-less integrated series of textbooks following the CUPM (Committee on the Undergraduate Program in Mathematics) guidelines in 1968–1969, as soon as they came out; not coincidentally, the Advanced Placement AB and BC tests for calculus started then too, and the textbook that Hal and I and Len Fellman wrote, Calculus of Elementary Functions, also followed the guidelines for the AB test—it was the first on the market, in fact. I have thus had a personal reason to follow trends in AP Calculus, and primary/secondary-school mathematics generally, through the years (at least until I retired and stopped teaching calculus forever; now my interest is more passive, and it takes something like this thread to revive it).
Judging from the first-year college students I taught (for 8 years at two Ivy League schools, a semester at Brandeis, and 25 years at a rather less stellar private university), most “high school calculus” (in the USA) is worse than a waste of time for most high school calculus students—whether it’s (formally) Advanced Placement or not. It certainly doesn’t serve to advance their mathematical understanding in such a way that they are better able to study other (post 17th century…) mathematics. (Neither do most college calculus courses, including most of the ones I taught.) Secondary-school mathematics courses that taught any of the various suggestions in earlier comments, if instructed by well-trained teachers, would be much better (in my opinion and that of a LOT of my colleagues over the years).
I’ll stop writing now before it drives me into shaking my fist at the clouds.
Ice Swimmer @16:
No, vectors are not standard in pre-college mathematics in the USA (and mostly don’t turn up at college until the second year, if then).
leerudolph @18
How do they teach physics in U.S. high schools, then? Is it all one-dimensional or do they teach vectors in (AP?) physics?
High School (non-GT/AP) physics is basically canned formulas. They’re all derived from at^2+bt+c, and my own teacher, knowing several of his students (including me) were taking Calc and/or pre-calc, actually showed how the 7 core formulas derived from that. There’s no “proof” for physics, which would require the calc level, just the application of them.
As for probability and statistics, there really should be a non-calc version taught in the lower grades. The only reason it is post-calc is because calculus is used in the proofs, but none of that is needed for the application. Just like non-calc mechanics, teaching the formulas and the application of them can go a long way to helping even non-college kids better deal with the world around them (and the ease to which media sources can lie).
In my school system, the standard college prep math ended with calculus, but statistics was optional. I’ve often thought that was backwards. In the thirty five years since I took it, I’ve never once felt a need for the calculus I learned, but I’ve often wished I had more statistics knowledge.
Ice Swimmer: We had linear algebra in high school in Canada, but it was new for most my classmates at university in the US. Similarly set theory.
madtom99@9, sugarfrosted@11,
Thanks for the link to the “Oxford Calculators” sugarfrosted; I hadn’t come across them. These historical abortive advances in maths (and in science and technology) are fascinating. I wonder if you’ve read The Archimedes Codex by Reviel Netz and William Noel, who have rediscovered and analysed a long-lost collection of works by Archimedes (“Codex C”), which shows just how far he’d got in developing calculus. Early moderns such as Galileo, Leibniz, Huygens, Fermat, Newton all based their work on what was known of Archimedes writings at the time (which came from Codixes A and B: C contains additional material); it’s interesting to speculate whether modern science would have developed faster, or differently, if C had been available to Galileo. Or, even more speculatively, if the intellectual tradition of the Hellenistic Age had continued to develop along the lines of Archimedes’s discoveries, and the Antikythera mechanism.
This doesn’t seem like a very useful guide for deciding where to stop when teaching generalist high school maths.
The infamous “New Math” was an attempt to introduce more modern mathematics into the classroom, and the usual suspects opposed it. There are similar smaller attempts from time to time.
I for one, wish students learned more about sets.
But this chart isn’t precisely correct. The Calc taught in high schools is based on 19th century thinking about continuity and limits, not the original formulation by Newton and Leibniz. And it includes results like the Intermediate Value Theorem that date from the 19th century.
Even Geometry is taught with a modern view of axiomatics and logic that would have been unfamiliar to mathematicians of the 17th century.
Yet another diagram of the history of ideas with a blatant anti-mediaeval bias! No hint of Algebra, Medeival Geometry, Fibonacci, the Merton Calculators, Grosseteste’s philosophy of infinity or just about anything between the collapse of Rome and the Renaissance.
Why, it’s almost as if there was some pervasive cultural imperialism alive and well in academia, which seeks to laud the ancients and align ourselves with them explicitly at the expense of our medieval forebears…
Most of school math builds on previous ideas to give a rounded understanding of arithmetic concepts. It all leads up to calculus because calculus is incredibly useful in scientific fields and probability.
The advanced math of later on is really much more specialized and not as useful (or at least not directly useful). Modular Arithmetic I think should be taught to middle/high schoolers because it’s good for basic calculation and computer science programming, but even the elementary concepts there were developed by the early Chinese.
numerobis @22
I’m not sure what the curriculum in upper secondary schools* is now, but here in Finland we had, in the AP-equivalent curriculum for maths, vectors in two dimensions (cross product and three dimensional vectors were kind of optional), but no matrices twenty years ago. I think the vectors were mainly taught so that they could be used in (AP) physics.
—
* = The system here is 9 years of compulsory comprehensive school and then either upper secondary school (3 years) leading to eligibility for all university education or vocational school leading to a vocation (carpenter, electrician, hairdresser etc) and eligibility to higher education in that field (an eletrician to an electrical engineer {a bachelor’s degree}).
Yeah PZ, just wear what you usually wear.
A friend of mine teaches calculus to undergrads at the local university – in classes of 400 or so at once.
She reports a lot of pressure to dumb it down, especially in testing, for the engineering students’ GPAs.
I went to elementary school during the “new math” craze of the 70s, so our first few years relied quite a bit on set theory. Is this no longer (or was never) the case in the US?
My math goes to algebra and no higher… I mathed as hard as I could and still don’t know what math is.
Dammit, that’s what I get for posting late at night and trying to edit the text before posting… obviously the “him” in my post at #5 ought to have been “Blaise Pascal”. (I cut a sentence out without checking to make sure it had the antecedent to any pronouns.)
@#31, Matthias Neeracher
Because Baby Boomer adults were confused by a math curriculum which wasn’t totally focused on “practical” skills (because of course nobody ever needs to know more math than it takes to make change or balance a checkbook*), New Math was kicked back out of the curriculum. Bits and pieces of it have gradually been reincorporated into the textbooks, because New Math makes it easier to learn higher mathematics (and, just incidentally, a few other minor and unimportant disciplines that are totally impractical, like, oh, computer science and physics) but most of it is gone again. Kids may get some set theory around Junior High School, but they won’t talk about sets again — let alone groups or fields or all the goodies which came out of Cantor’s study of infinite sets — until college, and then they basically have to be math majors to get there.
*I’m always astonished at the way people talk about “balancing a checkbook” as though it is some sort of sine qua non for either mathematical literacy or adulthood. Not only is it trivially easy — it uses nothing more than addition and subtraction, and the first page of the record book which comes with a new checking account tells you how to do it in most cases — but with every passing year it becomes more and more pointless. Most transactions in the average person’s bank account are now debit card transactions or transfers; not only is it inconvenient to constantly update your handwritten record in the checkbook, it’s likely to be less accurate because you may forget things. Much better to simply verify the totals — if you feel the need — using the statement. Do people in other disciplines have this sort of thing as well? I suppose we do have that with writing, since there’s the whole horror over cursive script being dropped, as though cursive wasn’t a waste of time in the modern world where most people need to learn to type, but does this happen in, say, physics classes?
The first time I ever balanced a chequebook was a couple months ago, for my business. And then, just because it was mildly convenient — the little form was right there, begging me to fill it out.
Ice Swimmer@28: we had linear algebra, up to inverting matrices via gaussian elimination to solve Ax = b. We were doing it by hand, so we maybe did a dimension 4 system once and generally just did dimension 2 or 3.
Except we wrote it funny, so I didn’t actually understand the formalism we had been using until I got most the way through my doctorate (and, actually, I still don’t completely get it; for some reason, we wrote A and b in a single matrix).
The Vicar (via Freethoughtblogs):
Yes, I think you could find pressure like that in all academic fields, a heavy emphasis on aspects that are immediately practical/useful, little focus on things that are considered a “waste of time” by some, caring most about applications related to commerce somehow, and so on. There are always questions like this: can I sell it, can this be my job, does it require a skill that’s instrumental for doing something else that I actually care about, etc. Knowing things for the sake of knowing them generally comes second to that. Pure math is perhaps more abstract or theoretical (read: “useless”) than some others, but it doesn’t seem really special in that regard.
numerobis @35:
Ah, but did you separate the b column from the rest with a dotted line? All the cool kids do that.
…I taught it that way a few times, purely because the textbook (which I had chosen and which had many features that really were good, as well as a few features—like that—which were “meh” as far as I was concerned) did it that way. I could probably even come up with a theoretical justification, if I had to (but one hasn’t occurred to me in the few seconds I’ve spent on it, so I’m quitting).
This reminds me of the Wolfram vision to teach math differently:
I never made it that far in math, but here’s the story of my run-in with linear algebra and how all the fun parts of life are optional: Years ago, while researching the inner workings of World of Warcraft UI addons with the intent of creating one of my own, I discovered that there was no DrawLine() function in the API. Which was shocking because there was a popular addon that had no problem drawing lots of lines.*
As it turns out, the only way to ‘draw’ a ‘line’ was to use linear algebra to pick four corners within a space tiled with an image from a file. So, I borrowed a book from a math tutor friend, and spent the winter holiday playing with Gaussian elimination and GeoGebra until I had solved it.
I was so happy with that experience that for the next year I set out to solve a long-standing mystery of mine: Just what the hell is going on with riffle shuffles and recurrence times with varying numbers of cards? Turns out to be a simple modular relationship, but it was a hard fight to get there using only high school algebra.
I guess I would have done better in school if it was all taught as a giant Stack Exchange Q&A centered around my various meanderings.
*If you want to see the way Recount does this, the relevant function in LibGraph-2.0.lua starts on line 1871 in rev 52 of the file.
leerudolph@37: yes, now that you mention it, we *were* taught to put a dotted line there!
The justification, I assume, is so that you don’t forget to also rearrange the b vector when pivoting.