The transitive property says that if A beats B and B beats C, then one would expect A to beat C. This seems quite obviously true and we use it in some form all the time. It is true for the real numbers where we think of ‘beats’ as ‘is greater than’ but is this transitive property true for all meanings of ‘beats’? Via Cory Doctorow, I came across this video of something called ‘Grime Dice’ that not only violate the transitive property (which is surprising in itself) but do so in very interesting ways.
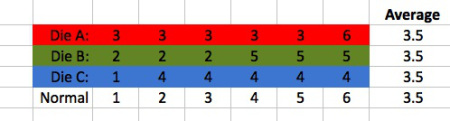
The numbers on the faces of the above dice all add up to different totals. What makes the result even more surprising is that the creator of the Protons for Breakfast Blog describes a a simplified version with three dice that have different numbering on the six faces such that they have the same average value of 3.5 as a normal die.
He says that the same transitive violating property repeats itself even with these three dice. In head to head competition, on average the red die A will beat the green die which in turn will beat the blue die, which will beat the red die.
In addition, when the number of die of each color is doubled, the sequence is reversed with the pair of red dice losing to the green dice that will lose to the blue dice that will lose to the red dice.
Incidentally you may remember James Grime from the above video as the mathematician who explained the proof that the answer to the Sudoku problem is 17.

Shouldn’t rock-paper-scissor be another example of such non-transitive games ?
There is a whole field of mathematics that addresses this, called abstract algebra. It turns out that numbers represent a very specific special case of set theory, defined by a long list of properties that may or may not be present.
One of the first examples when I took abstract algebra was a cardboard cutout of a triangle, each with a different color on each of its edges on one side, and different colors on each edge on the other side. Define the cutout’s “value” as the upward color on the side closest to you. Define two basic operations, rotation and flip. Rotation involves turning the triangle 120 degrees parallel to your surface, so that an adjacent side is the new value. Flip involves turning the triangle 180 degress perpendicular to your surface, so that same edge, but the other side, is the new value. Rotation can be positive (to the right) or negative (to the left.)
With only six possible values and two operations, you can build a simple mathematical system that is neither commutative nor transitive.
That was also my first thought.
It is true that you can always define three quantities that operate in such a circle, like the rock-paper-scissors.
It is the fact that with these dice the property emerges out of a set of numbers, and that there is a reversal of their order when the number of dice is doubled is what I thought makes it interesting.
I think you might be slightly confused here. It’s true that S3 (the symmetric group on three elements, which you just described) is noncommutative, but it isn’t “nontransitive” because transitivity, as used here, is a property of a relation, not a group.
I’m not actually aware of any well-developed mathematical theory of nontransitive dice and other nontransitive games. Sadly, I think they are widely viewed as little more than a curiosity.
Such dice also come in sets of four, known as Efron’s Dice. Those are the ones I’m familiar with.
http://mathworld.wolfram.com/EfronsDice.html
http://en.wikipedia.org/wiki/Nontransitive_dice
If a person wanted to make such dice, there are companies on the internet which sell unlabelled dice that either have blank faces (to put stickers on) or surfaces that can be written on.
http://www.blankdice.co.uk/
http://www.gmdice.com/catalogsearch/result/?q=blank+dice
Those links are not plugs for the companies, theirs were the first that appeared in a search.
Thanks for posting these links. I read that Martin Gardner had also written about this way back in 1970: “Mathematical Games: The Paradox of the Nontransitive Dice and the Elusive Principle of Indifference.” Scientific American 223, 110-114, Dec. 1970.
I havent’ read the article as yet, though.