Are you into cubes? I made a reference sheet / infographic of the cube’s symmetry group, and every single subgroup. There are 98 subgroups, so… I hope you like lots of cubes.
Are you into cubes? I made a reference sheet / infographic of the cube’s symmetry group, and every single subgroup. There are 98 subgroups, so… I hope you like lots of cubes.
My previous post, “Solving fractal mazes” is a prerequisite to this one. Fair warning, this will be long and dense.
Fractal mazes contain infinite paths, but the only solutions permitted are finite. Some people find that disappointing. What’s the point of all that extra maze if we don’t get to traverse it? So my goal is to come up with a variant ruleset for fractal mazes that permits and formalizes infinite solutions. In fact, I will propose two distinct rulesets, provocatively titled Countably Infinite Fractal Mazes and Cantor Fractal Mazes.
What are fractal mazes?
Fractal Mazes are a type of maze popularized (or invented?) by Mark J. P. Wolf, published in the Mathpuzzle blog in 2003. A fractal maze is a maze that contains nested copies of itself.
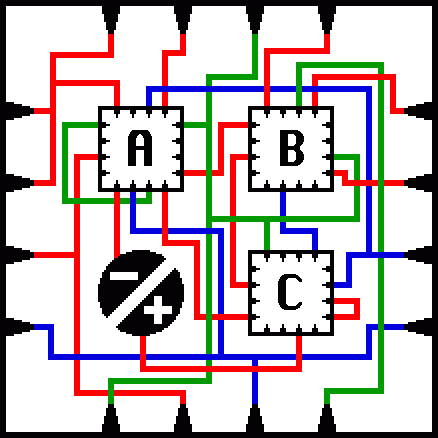
“Small Fractal Maze”. Credit: Mark J. P. Wolf. Source: Mathpuzzle
Fractal Mazes are typically visually represented as a sort of circuit diagram. In the above image, the goal is to find a path between the “+” and “-” by following the colored wires. The wires are color coded in order to clearly indicate where paths cross over/under each other. The three modules, labeled A, B, and C, are each copies of the entire maze. However, the start and finish only exist in the largest copy of the maze. So however deep you go into the fractal, you must eventually climb all the way back up again.
I invented a game, and it goes like this. We’re going to pick a 20 digit number by taking turns choosing each digit. I choose the first digit, then you choose the second digit, I choose the third and so on. Once we’ve chosen all the digits, we use our number as the seed to a random number generator. The random number generator picks a number between 0 and 1, and if the number is greater than 0.5 then I win; if it’s less than 0.5 then you win.
Obviously this isn’t meant to be a “fun” game, it’s more of an open-ended math problem. What’s the strategy? Is there a strategy? Who wins?
The idea behind the random number generator, is that it’s deterministic, and yet opaque. Given any particular seed, the random number generator will consistently pick the same result—either you win, or I do. But there’s no particular pattern to it. It behaves as if the result were randomly chosen. The only way to predict the game’s outcome is to individually plug in each random seed into the random number generator. However, this might be intractable, as there are 10^20 possible seeds.
This game is deterministic, finite, and perfect information—much like Chess. However, it appears that the only real strategy is brute force, by plugging in seeds into the random number generator.
A big reason why I enjoy dabbling in electronic music production is that it’s a way of directly transforming math into physical sensation. It’s math you can literally hear. One of the most incredible examples is FM synthesis.
FM stands for frequency modulation. That means that you change the frequency of a note over time, generally in a cyclical pattern. Our ears interpret frequency as pitch, so this may sound like a pitch that fluctuates over time. However, if the fluctuation occurs fast enough, our ears can no longer track it, and it begins to sound completely different.
Try listening to these demos:
Demo 1

Aperiodic Chevron Tessellation, designed by me
Did you hear? Someone discovered an aperiodic monotile! Obviously, these are origami life goals. And, I’m making it out like a joke, but I’m pretty sure I’m not the only origamist who was thinking that.
Oh, but this origami isn’t the aperiodic monotile. Instead, I read their paper, and was inspired to create a different aperiodic tiling. And in the mean time, I learned how an aperiodic tile ticks.
In my time as a puzzle enthusiast, one of the puzzles I encountered was called the ant and the rubber band. It was only later that I realized that this puzzle had some cosmic significance.
Problem Statement
We have an ant that is trying to crawl from one end of a rubber band to the other. But as the ant crawls, the rubber band also stretches out. The ant crawls one centimeter per second. The rubber band starts out one meter long, and stretches out one meter per second. This is one of those magical math rubber bands that can stretch indefinitely. Let’s just say the ant is mathemagical too. Will the ant ever reach the end?
At first glance, it looks bad for the ant. The ant crawls crawls one centimeter closer, but falls a whole meter back. So the ant is losing about 99 cm per second. That doesn’t sound like a path to victory.
